In this section we will discuss possibilities regarding statistical inference for quantile regression models. Although there are nearly no usable finite sample results for statistical inference compared to the often used theory of least squares under the normality assumption, the asymptotic theory offers several competing methods, namely tests based on the Wald statistics, rank tests, and likelihood ratio-like tests. Some of them are discussed in this section.
The asymptotic behavior of ordinary sample quantiles generalizes relatively easily
to the quantile regression case. A fundamental result was derived
in Koenker and Bassett (1978). Let
![]() be the quantile regression process
and consider the classical regression model
be the quantile regression process
and consider the classical regression model
The situation is little bit more complicated in the case of non-i.i.d. errors,
but the normality of the quantile regression estimator is preserved under
heteroscedasticity. If we denote the estimate of coefficients for
![]() by
by
![]() , then for
, then for
![]()
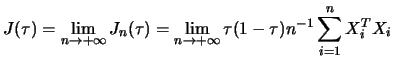
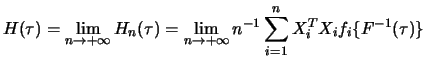
As was already mentioned in the previous section, the asymptotic
normality of quantile regression estimates gives us the possibility
to test various linear
hypotheses formulated through regression quantiles by means of the
Wald test. For a general linear hypothesis about the vector
![]()
| (1.13) |
| (1.14) |
To present a possible application of this test procedure, let us explain a simple test of heteroscedasticity. Following Koenker and Bassett (1982a), homoscedasticity is equivalent to the equality of slope parameters across quantiles. Consider, for example, model (1.3)
The classical theory of rank test (Hájek and Šidák; 1967) employs the rankscore functions
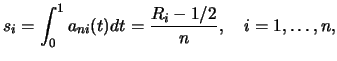 |
(1.16) |
| (1.17) | |||
The uncovered link to rankscore tests enabled to construct tests of significance
of regressors in quantile regression without necessity to estimate some nuisance parameters
(such as ![]() in the case of the Wald test). Given the model
in the case of the Wald test). Given the model
![]() ,
Gutenbrunner, Jurecková, Koenker, and Portnoy (1993) designed a test of hypothesis
,
Gutenbrunner, Jurecková, Koenker, and Portnoy (1993) designed a test of hypothesis
![]() based on the regression rankscore process. It is constructed in the following way: first,
compute
based on the regression rankscore process. It is constructed in the following way: first,
compute
![]() at the restricted model
at the restricted model
![]() and the corresponding
rankscores vector
and the corresponding
rankscores vector
![]() .
Next, form the vector
.
Next, form the vector
 rrstest
, which requires the two parts of the matrix
x and the vector y on input.
Optionally, you can specify the type of the score generating function to be
used
(see Section 1.5 for more details); the Wilcoxon scores are
employed by default. For demonstration of the quantlet, let us use again a
simulated data set--we generate a pseudo-random
rrstest
, which requires the two parts of the matrix
x and the vector y on input.
Optionally, you can specify the type of the score generating function to be
used
(see Section 1.5 for more details); the Wilcoxon scores are
employed by default. For demonstration of the quantlet, let us use again a
simulated data set--we generate a pseudo-random
; simulate data matrix n = 100 randomize(1101) x = matrix(n) ~ uniform(n,2) ; generate y1 and y2 y1 = x[,1] + 2*x[,2] - x[,3] + normal(n) y2 = x[,1] + 2*x[,2] + normal(n) ; test the hypothesis that the coefficient of x[,3] is zero ; first case chi1 = rrstest(x[,1:2], x[,3], y1) chi1 cdfc(chi1,1) ; second case chi2 = rrstest(x[,1:2], x[,3], y2) chi2 cdfc(chi2,1)
Contents of chi1 [1,] 19.373 Contents of cdfc [1,] 0.99999 Contents of chi2 [1,] 0.018436 Contents of cdfc [1,] 0.10801
The existence of a testing strategy for quantile regression motivated
the search for a reverse procedure that would
provide a method for estimating confidence intervals without
actual knowledge of the asymptotic covariance matrix. Quite general results in
this area were derived in Hušková (1994). Although the
computation of these confidence intervals is rather
difficult, there are some special cases for which the procedure is
tractable (Koenker; 1994). An adaptation of the technique for
non-i.i.d. errors have been done recently.
Now, it was already mentioned that quantlet
 rqfit
can compute also
confidence intervals for quantile regression estimates. This is done by the
above mentioned method of inverting rank tests,
which has several practical implications. Above all, the computation of
confidence intervals at an exact significance level
rqfit
can compute also
confidence intervals for quantile regression estimates. This is done by the
above mentioned method of inverting rank tests,
which has several practical implications. Above all, the computation of
confidence intervals at an exact significance level ![]() would require
knowledge of the entire quantile regression process
would require
knowledge of the entire quantile regression process
![]() . This is not possible because we always work
with finite samples, hence we have only an approximation of the process in the
form
. This is not possible because we always work
with finite samples, hence we have only an approximation of the process in the
form
![]() . Therefore, two
confidence intervals are computed for every parameter at a given significance
level
. Therefore, two
confidence intervals are computed for every parameter at a given significance
level ![]() (parameter alpha)--the largest one with true
significance level higher than
(parameter alpha)--the largest one with true
significance level higher than ![]() , let us call it
, let us call it ![]() , and the smallest
one with true significance level lower than
, and the smallest
one with true significance level lower than ![]() ,
, ![]() . Then, according to
the value of parameter interp, various results are returned. If its
value is nonzero or the parameter is not specified, e.g.,
. Then, according to
the value of parameter interp, various results are returned. If its
value is nonzero or the parameter is not specified, e.g.,
z = rqfit(x, y, 0.5, 1)then the bounds of the returned intervals are interpolated from the lower and upper bounds of the pairs of intervals, and the result in z.intervals is a
z = rqfit(x, y, 0.5, 1, 1, 0)z.intervals is a
Finally, before closing this topic, we make one small remark on iid switch. Its value specifies, whether the procedure should presume i.i.d. errors (this is the default setting), or whether it should make some non-i.i.d. errors adjustments. We can disclose the effect of this parameter using the already discussed nicfoo data. The data seem to exhibit some kind of heteroscedasticity (as is often the case if the set of significant explanatory variables involve individuals with diverse levels of income), see Figure 1.4.
![\includegraphics[scale=0.6]{qr07}](xaghtmlimg232.gif)
|
To compare the resulting confidence intervals for median regression under the i.i.d. errors assumption and without it, you can type at the command line or in the editor window
data = read("nicfoo")
x = matrix(rows(data)) ~ data[,1] ~ (data[,1]^2)
y = data[,2]
;
z = rqfit(x,y,0.5,1,0.1,1)
z.intervals
;
z = rqfit(x,y,0.5,1,0.1,0)
z.intervals
Once you run this example, the output window will contain the following results:
Contents of intervals [1,] 0.12712 0.13194 [2,] 1.1667 1.2362 [3,] -0.24616 -0.24608 Contents of intervals [1,] 0.024142 0.20241 [2,] 1.0747 1.3177 [3,] -0.29817 -0.2014Please, notice the difference between the first group of intervals (i.i.d. errors assumption) and the second one.