2.5 Interval Estimation

The LS and ML methods developed in previous sections allow us to obtain a point estimate of the parameters of the model. However, even if the estimator satisfies the desirable properties, there is some probability that it will be quite erroneous, because it tries to infer a population value from a sample. Thus, a point estimate does not provide any information on the likely range of error. The estimator should be as accurate as possible (i.e., the range of error as small as possible), and this accuracy can be quantified through the variance (or standard deviation) of the estimator. Nevertheless, if we know the sample distribution of the estimator, there is a more structured approach of presenting the accuracy measure which consists in constructing a confidence interval.

A confidence interval is defined as a range of values that is likely to include the true value of the unknown parameter. The confidence interval means that, if we have different samples, and in each case we construct the confidence intervals, then we expect that about $100(1-\epsilon)$ percent of them will contain the true parameter value. The probability amount $(1-\epsilon)$ is known as the level of confidence.

2.5.1 Interval Estimation of the Coefficients of the MLRM

As we have mentioned earlier, in order to obtain the interval estimation, we must know the sample probability distribution of the corresponding estimator. Result (2.74) allows us to obtain such a distribution for every element of the $\hat{\beta}$ vector as:

$$\begin{array}{cc} \hat{\beta}_{j}\sim N(\beta_{j},\sigma^{2}((X^{\top }X)^{-1})_{jj})& (j=1,\ldots,k) \end{array}$$ (2.120)

and thus,

$$\frac{\hat{\beta}_{j}-\beta_{j}}{\sqrt{\sigma^{2}((X^{\top }X)^{-1})_{jj}}}\sim N(0,1)$$ (2.121)

However, using (2.121), we can see that, in addition to $\beta_{j}$ (whose interval estimation we want to calculate) $\sigma ^{2}$ is also unknown. In order to solve this problem, we must remember (2.77) and (2.78), in such a way that:

$$\frac{\hat{u}^{\top }\hat{u}}{\sigma^{2}}=\frac{u^{\top }Mu}{\sigma^{2}}\sim\chi^{2}_{n-k}$$

Given the independence between this random variable and that of (2.121) (proved in Hayashi (2000)), we can write:

$$\frac{\frac{\hat{\beta}_{j}-\beta_{j}}{\sqrt{\sigma^{2}((X^{\top ... ...\top }X)^{-1})_{jj}}}=\frac{\hat{\beta}_{j}-\beta_{j}}{\hat{s}_{j}}\sim t_{n-k}$$ (2.122)

which is distributed as a t-Student with $(n-k)$ degrees of freedom, where $\hat{s}_{j}$ denotes the estimated standard deviation of $\hat{\beta}_{j}$. From (2.122), and with a fixed level of confidence $(1-\epsilon)$ (or alternatively a level of significance $\epsilon$), we have

$$\begin{array}{cc} Pr[-t_{\frac{\epsilon}{2}}<\frac{\hat{\beta... ...<t_{\frac{\epsilon}{2}}]=1-\epsilon& (j=1,\ldots,k) \end{array}$$ (2.123)

and then,

$$\begin{array}{cc} \hat{\beta}_{j}\pm t_{\frac{\epsilon}{2}}\hat{s}_{j}& (j=1,\ldots,k) \end{array}$$ (2.124)

which provides the general expression of the $100(1-\epsilon)$ percent confidence interval for $\beta_{j}$. Given that $\hat{s}_{j}$ is a component of the interval, the amplitude of the interval is a measure of the how accurate the estimator is.

2.5.2 Interval Estimation of $\sigma ^{2}$

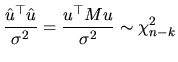
In order to obtain the interval estimation of $\sigma ^{2}$ we take the distribution given in (2.78) and the expression of the OLS estimator of $\sigma ^{2}$ given in (2.34), in such a way that,

$$\frac{\hat{u}^{\top }\hat{u}}{\sigma^{2}}=\frac{(n-k)\hat{\sigma}^{2}}{\sigma^{2}}\sim \chi^{2}_{n-k}$$ (2.125)

so that, for a fixed level of significance $\epsilon$, or level of confidence $(1-\epsilon)$ the confidence interval is constructed as follows:

$$Pr[\chi^{2}_{1-\frac{\epsilon}{2}}<\frac{(n-k)\hat{\sigma}^{2}}{\sigma^{2}}<\chi^{2}_{\frac{\epsilon}{2}}]=1-\epsilon$$ (2.126)

and the interval estimation of $\sigma ^{2}$ is given by:

$$\left[\frac{(n-k)\hat{\sigma}^{2}}{\chi^{2}_{\frac{\epsilon}{2}}};\frac{(n-k)\hat{\sigma}^{2}}{\chi^{2}_{1-\frac{\epsilon}{2}}}\right]$$ (2.127)

2.5.3 Example

From our consumption function example, we now want to calculate the interval confidence for the three coefficients ($\beta_{1}$, $\beta_{2}$, $\beta_{3}$) and the dispersion parameter $\sigma ^{2}$. In each case, we calculate the interval for levels of confidence of 90 and 95 percent ($\epsilon$=0.1 and 0.05). The following quantlet allow us to obtain the previous information

XEGmlrm04.xpl