- ... universally11.1
- In
this chapter, the denomination universal is used in the sense
of uniformly over all distributions.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
varies11.2
- To impose the stationarity constraint when the order of the
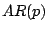 model varies,
it is necessary to reparameterise this model in terms of either the
partial autocorrelations or of the
roots of the associated lag polynomial. (See, e.g.,
[35], Sect. 4.5.)
model varies,
it is necessary to reparameterise this model in terms of either the
partial autocorrelations or of the
roots of the associated lag polynomial. (See, e.g.,
[35], Sect. 4.5.)
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... integrals.11.3
- In this
presentation of Bayes factors, we completely bypass the methodological
difficulty of defining
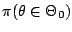 when
when 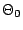 is
of measure 0 for the original prior
is
of measure 0 for the original prior 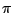 and refer the reader to
Robert (2001, Section 5.2.3) for proper coverage of this issue.
and refer the reader to
Robert (2001, Section 5.2.3) for proper coverage of this issue.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... density11.4
- The prior distribution can be used for importance
sampling only if it is a proper prior and not a
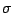 -finite
measure.
-finite
measure.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... methods.11.5
- The constant order of the Monte Carlo error does not
imply that the computational effort remains the same as the dimension
increases, most obviously, but rather that the decrease (with
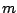 ) in
variation has the rate
) in
variation has the rate 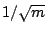 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... simulations.11.6
- The
empirical (Monte Carlo) confidence interval is not to be confused with
the asymptotic confidence interval
derived from the normal approximation. As discussed in Robert and
Casella (2004, Chap. 4), these two intervals may differ considerably
in width, with the interval derived from the CLT being much more
optimistic!
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... quickly.11.7
- An alternative to the simulation
from one
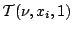 distribution that does not require
an extensive study on the most appropriate
distribution that does not require
an extensive study on the most appropriate 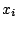 is to use a mixture
of the
is to use a mixture
of the
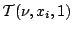 distributions. As seen in
Sect. 11.5.2, the weights of this mixture can even be
optimised automatically.
distributions. As seen in
Sect. 11.5.2, the weights of this mixture can even be
optimised automatically.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... Sect. 10.3.2).11.8
- Even in the simple case of the probit model,
MCMC algorithms do not always converge very quickly, as shown in
[37] (2004, Chap. 14).
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... occur.11.9
- It is quite interesting to see that
the mixture Gibbs sampler suffers from the same pathology as the EM
algorithm, although this is not surprising given that it is based on
the same completion scheme.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... moves.11.10
- This
wealth of possible alternatives to the completion Gibbs sampler is
a mixed blessing in that their range, for instance the scale of the
random walk proposals, needs to be scaled properly to avoid
inefficiencies.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... distribution?11.11
- Early proposals to solve the varying dimension
problem involved saturation schemes where all the parameters for all
models were updated deterministically ([9]), but
they do not apply for an infinite collection of models and they need
to
be precisely calibrated to achieve a sufficient amount of moves
between models.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ....11.12
- For a simple proof that the
acceptance probability guarantees that the stationary distribution is
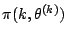 , see Robert and Casella (2004, Sect. 11.2.2).
, see Robert and Casella (2004, Sect. 11.2.2).
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ....11.13
- In the birth acceptance probability,
the factorials
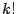 and
and 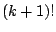 appear as the numbers of ways of
ordering the
appear as the numbers of ways of
ordering the 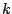 and
and 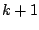 components of the mixtures. The ratio
cancels with
components of the mixtures. The ratio
cancels with 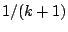 , which is the probability of selecting
a particular component for the death step.
, which is the probability of selecting
a particular component for the death step.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... distributions.11.14
- The ''sequential'' denomination in the
sequential Monte Carlo methods
thus refers to the algorithmic part, not to the statistical part.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... a proposal.11.15
- Using a Gaussian non-parametric kernel
estimator amounts to (a) sampling from the
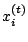 's with
equal weights and (b) using a normal random walk move from the
selected
's with
equal weights and (b) using a normal random walk move from the
selected 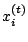 , with standard deviation equal to the
bandwidth of the kernel.
, with standard deviation equal to the
bandwidth of the kernel.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... resampling.11.16
- When the survival rate
of a proposal distribution is null, in order to avoid the complete
removal of a given scale
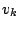 , the corresponding number
, the corresponding number 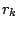 of
proposals with that scale is set to a positive value, like
of
proposals with that scale is set to a positive value, like
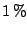 of the sample
size.
of the sample
size.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.