As described precisely in Chap. III.3 and in [37], MCMC methods try to overcome the limitation of regular Monte Carlo methods by mean of a Markov chain with stationary distribution the posterior distribution. There exist rather generic ways of producing such chains, including Metropolis-Hastings and Gibbs algorithms. Besides the fact that stationarity of the target distribution is enough to justify a simulation method by Markov chain generation, the idea at the core of MCMC algorithms is that local exploration, when properly weighted, can lead to a valid representation of the distribution of interest, as for instance, the Metropolis-Hastings algorithm.
The Metropolis-Hastings, presented in [37] and
Chap. II.3, offers
a straightforward solution to the problem of simulating from the
posterior distribution
![]() : starting from an arbitrary point
: starting from an arbitrary point
![]() , the corresponding Markov chain explores the surface of
this posterior distribution by a random walk proposal
, the corresponding Markov chain explores the surface of
this posterior distribution by a random walk proposal
![]() that progressively visits the whole range of
the possible values of
that progressively visits the whole range of
the possible values of ![]() .
.
Metropolis-Hastings Algorithm
At iteration ![]()
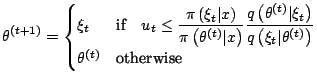 |
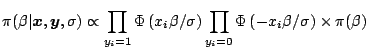 |
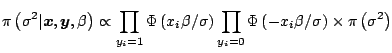 |
Obviously, this is only a toy example and more realistic probit models do not fare so well with down-the-shelf random walk Metropolis-Hastings algorithms, as shown for instance in [32] (see also [37], Sect. 10.3.2).11.8
![\includegraphics[width=11.4cm]{text/3-11/probit1.eps}](img6318.gif)
|
![\includegraphics[width=8.3cm]{text/3-11/probste.eps}](img6319.gif)
|
The difficulty inherent to random walk Metropolis-Hastings algorithms
is the scaling
of the proposal distribution: it must be adapted to the shape of the
target distribution so that, in a reasonable number of steps, the
whole support of this distribution can be visited. If the scale of the
proposal is too small, this will not happen as the algorithm stays
''too local'' and, if there are several modes on the posterior, the
algorithm may get trapped within one modal region because it cannot
reach other modal regions with jumps of too small magnitude. The
larger the dimension ![]() is, the harder it is to set up the right
scale, though, because
is, the harder it is to set up the right
scale, though, because
The Gibbs sampler is a definitely attractive algorithm for Bayesian problems because it naturally fits the hierarchical structures so often found in such problems. ''Natural'' being a rather vague notion from a simulation point of view, it routinely happens that other algorithms fare better than the Gibbs sampler. Nonetheless, Gibbs sampler is often worth a try (possibly with other Metropolis-Hastings refinements at a later stage) in well-structured objects like Bayesian hierarchical models and more general graphical models.
A very relevant illustration is made of latent variable models, where the observational model is itself defined as a mixture model,
 |
Latent Variable Gibbs Algorithm
At iteration ![]()
While we could have used the probit case as an illustration (Example 11), as done in Chap. II.3, we choose to pick the case of mixtures (Example 6) as a better setting.
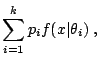 |
However, mixtures are also customarily used for density
approximations, as a limited dimension proxy to non-parametric
approaches. In such cases, the components of the mixture and even the
number ![]() of components in the mixture are often meaningless for the
problem to be analysed. But this distinction between natural and
artificial completion (by the
of components in the mixture are often meaningless for the
problem to be analysed. But this distinction between natural and
artificial completion (by the ![]() 's) is lost to the MCMC sampler,
whose goal is simply to provide a Markov chain that converges to the
posterior as stationary distribution. Completion is thus, from
a simulation point of view, a mean to generate such
a chain.
's) is lost to the MCMC sampler,
whose goal is simply to provide a Markov chain that converges to the
posterior as stationary distribution. Completion is thus, from
a simulation point of view, a mean to generate such
a chain.
The most standard Gibbs sampler for mixture models
([11]) is thus based on the successive
simulation of the ![]() 's and of the
's and of the ![]() 's, conditional on one
another and on the data:
's, conditional on one
another and on the data:
As an illustration, consider the case of a normal mixture with two components, with equal known variance and fixed weights,
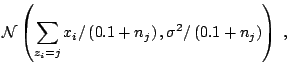 |
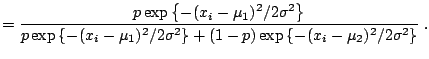 |
This experiment gives a wrong sense of safety, though, because it does
not point out the fairly large dependence of the Gibbs sampler to the
initial conditions, already signaled in [11]
under the name of trapping states.
Indeed, the conditioning of
![]() on
on
![]() implies
that the new simulations of the means will remain very close to the
previous values, especially if there are many observations, and thus
that the new allocations
implies
that the new simulations of the means will remain very close to the
previous values, especially if there are many observations, and thus
that the new allocations
![]() will not differ much from the
previous allocations. In other words, to see a significant
modification of the allocations (and thus of the means) would require
a very very large number of iterations. Figure 11.10
illustrates this phenomenon for the same sample as in
Fig. 11.9, for a wider scale: there always exists
a second mode in the posterior distribution, which is much lower than
the first mode located around
will not differ much from the
previous allocations. In other words, to see a significant
modification of the allocations (and thus of the means) would require
a very very large number of iterations. Figure 11.10
illustrates this phenomenon for the same sample as in
Fig. 11.9, for a wider scale: there always exists
a second mode in the posterior distribution, which is much lower than
the first mode located around ![]() . Nonetheless, a Gibbs
sampler initialized close to the second and lower mode will not be
able to leave the vicinity of this (irrelevant) mode, even after
a large number of iterations. The reason is as given above: to jump to
the other mode, a majority of
. Nonetheless, a Gibbs
sampler initialized close to the second and lower mode will not be
able to leave the vicinity of this (irrelevant) mode, even after
a large number of iterations. The reason is as given above: to jump to
the other mode, a majority of ![]() 's would need to change
simultaneously and the probability of such a jump is too close to 0
to let the event occur.11.9
's would need to change
simultaneously and the probability of such a jump is too close to 0
to let the event occur.11.9
![\includegraphics[width=11.7cm]{text/3-11/gib+mix2.eps}](img6344.gif) |
![\includegraphics[width=11.5cm]{text/3-11/wrongmix.eps}](img6345.gif)
|
This example illustrates quite convincingly that, while the completion is natural from a model point of view (since it is a part of the definition of the model), it does not necessarily transfer its utility for the simulation of the posterior. Actually, when the missing variable model allows for a closed form likelihood, as is the case for mixtures, probit models (Examples 11 and 14) and even hidden Markov models (see [8]), the whole range of the MCMC technology can be used as well. The appeal of alternatives like random walk Metropolis-Hastings schemes is that they remain in a smaller dimension space, since they avoid the completion step(s), and that they are not restricted in the range of their moves.11.10
![\includegraphics[width=11.1cm]{text/3-11/rwMix.eps}](img6349.gif)
|
The secret of a successful MCMC implementation in such latent variable models is to maintain the distinction between latency in models and latency in simulation (the later being often called use of auxiliary variables). When latent variables can be used with adequate mixing of the resulting chain and when the likelihood cannot be computed in a closed form (as in hidden semi-Markov models, [6]), a Gibbs sampler is a still simple solution that is often easy to simulate from. Adding well-mixing random walk Metropolis-Hastings steps in the simulation scheme cannot hurt the overall mixing of the chain ([37], Chap. 13), especially when several scales can be used at once (see Sect. 11.5). A final word is that the completion can be led in an infinity of ways and that several of these should be tried or used in parallel to increase the chances of success.
As described in Sect. 11.2.3, model choice is
computationally different from testing in that it considers at once a
(much) wider range of models
![]() and parameter
spaces
and parameter
spaces ![]() .
Although early approaches could only go through a pedestrian pairwise
comparison, a more adequate perspective is to envision the model index
.
Although early approaches could only go through a pedestrian pairwise
comparison, a more adequate perspective is to envision the model index
![]() as part of the parameter to be estimated, as in (11.3).
The (computational) difficulty is that we are then dealing with
a possibly infinite space that is the collection of unrelated sets:
how can we then simulate from the corresponding
distribution?11.11
as part of the parameter to be estimated, as in (11.3).
The (computational) difficulty is that we are then dealing with
a possibly infinite space that is the collection of unrelated sets:
how can we then simulate from the corresponding
distribution?11.11
The MCMC solution proposed
by [20] is called reversible jump MCMC, because
it is based on a reversibility constraint on the transitions
between the sets ![]() . In fact, the only real difficulty
compared with previous developments is to validate moves (or
jumps) between the
. In fact, the only real difficulty
compared with previous developments is to validate moves (or
jumps) between the ![]() 's, since proposals restricted
to a given
's, since proposals restricted
to a given ![]() follow from the usual (fixed-dimensional)
theory. Furthermore, reversibility can be processed at
a local level: since the model indicator
follow from the usual (fixed-dimensional)
theory. Furthermore, reversibility can be processed at
a local level: since the model indicator ![]() is a integer-valued
random variable, we can impose reversibility for each pair
is a integer-valued
random variable, we can impose reversibility for each pair ![]() of possible values of
of possible values of ![]() . The idea at the core of reversible jump
MCMC is then to supplement each of the spaces
. The idea at the core of reversible jump
MCMC is then to supplement each of the spaces
![]() and
and
![]() with adequate artificial spaces in order to create
a bijection
between them. For instance, if
with adequate artificial spaces in order to create
a bijection
between them. For instance, if
![]() and if the move from
and if the move from
![]() to
to
![]() can be represented by
a deterministic transformation of
can be represented by
a deterministic transformation of
![]()
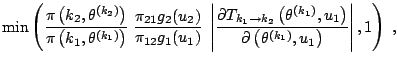 |
The pseudo-code representation of Green's algorithm is thus as follows:
Green's Algorithm
At iteration ![]() , if
, if
![]() ,
,
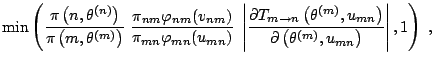 |
As for previous methods, the implementation of this algorithm requires a certain skillfulness in picking the right proposals and the appropriate scales. This art of reversible jump MCMC is illustrated on the two following examples, extracted from Robert and Casella (2004, Sect. 14.2.3).
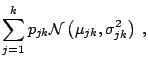 |
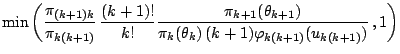 |
||
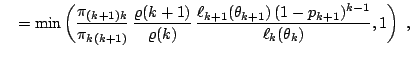 |
While this proposal can work well in some setting, as in Richardson and Green (1997) when the prior is calibrated against the data, it can also be inefficient, that is, leading to a high rejection rate, if the prior is vague, since the birth proposals are not tuned properly. A second proposal, central to the solution of [34], is to devise more local jumps between models, called split and combine moves, since a new component is created by splitting an existing component into two, under some moment preservation conditions, and the reverse move consists in combining two existing components into one, with symmetric constraints that ensure reversibility. (See, e.g., [37], for details.)
Figures 11.12-11.14 illustrate the
implementation of this algorithm for the so-called Galaxy dataset used
by [34] (see also [38]), which
contains ![]() observations on the speed of galaxies. On
Fig. 11.12, the MCMC output on the number of components
observations on the speed of galaxies. On
Fig. 11.12, the MCMC output on the number of components
![]() is represented as a histogram on
is represented as a histogram on ![]() , and the corresponding
sequence of
, and the corresponding
sequence of ![]() 's. The prior used on
's. The prior used on ![]() is a uniform distribution on
is a uniform distribution on
![]() : as shown by the lower plot, most values of
: as shown by the lower plot, most values of ![]() are
explored by the reversible jump algorithm, but the upper bound does
not appear to be restrictive since the
are
explored by the reversible jump algorithm, but the upper bound does
not appear to be restrictive since the ![]() 's hardly ever reach
this upper limit. Figure 11.13 illustrates the fact that
conditioning the output on the most likely value of
's hardly ever reach
this upper limit. Figure 11.13 illustrates the fact that
conditioning the output on the most likely value of ![]() (
(![]() here) is
possible. The nine graphs in this figure show the joint variation of
the three types of parameters, as well as the stability of the Markov
chain over the
here) is
possible. The nine graphs in this figure show the joint variation of
the three types of parameters, as well as the stability of the Markov
chain over the
![]() iterations: the cumulated averages are
quite stable, almost from the start.
iterations: the cumulated averages are
quite stable, almost from the start.
The density plotted on top of the histogram in Fig. 11.14
is another good illustration of the inferential possibilities offered
by reversible jump algorithms, as a case of model
averaging:
this density is obtained as the average over iterations ![]() of
of
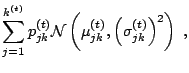 |
![\includegraphics[width=11.7cm]{text/3-11/galakhist.eps}](img6396.gif) |
![\includegraphics[width=11.7cm]{text/3-11/galtetahis.eps}](img6397.gif)
|
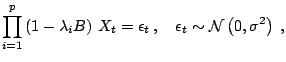 |
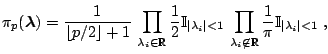 |
Once again, a simple choice is to use a birth-and-death scheme where the birth moves either create a real or two conjugate complex roots. As in the birth-and-death proposal for Example 17, the acceptance probability simplifies quite dramatically since it is for instance
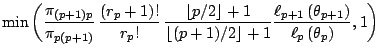 |
Figure 11.15 presents some views of the corresponding reversible
jump MCMC algorithm. Besides the ability of the algorithm to explore
a range of values of ![]() , it also shows that Bayesian inference using
these tools is much richer, since it can, for instance, condition on
or average over the order
, it also shows that Bayesian inference using
these tools is much richer, since it can, for instance, condition on
or average over the order ![]() , mix the parameters of different models
and run various tests on these parameters. A last remark on this graph
is that both the order and the value of the parameters are well
estimated, with a characteristic trimodality on the histograms of the
, mix the parameters of different models
and run various tests on these parameters. A last remark on this graph
is that both the order and the value of the parameters are well
estimated, with a characteristic trimodality on the histograms of the
![]() 's, even when conditioning on
's, even when conditioning on ![]() different from
different from ![]() , the
value used for the simulation.
, the
value used for the simulation.
![\includegraphics[width=11.7cm]{text/3-11/plain.eps}](img6408.gif) |