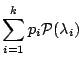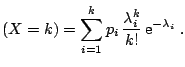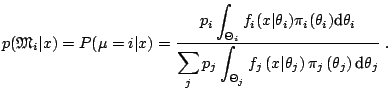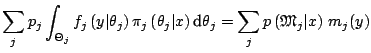



Next: 11.3 Monte Carlo Methods
Up: 11. Bayesian Computational Methods
Previous: 11.1 Introduction
Subsections
11.2 Bayesian Computational Challenges
Bayesian Statistics being a complete inferential methodology, its
scope encompasses the whole range of standard statistician inference
(and design), from point estimation to testing, to
model selection, and to non-parametrics. In principle, once a prior
distribution has been chosen on the proper space, the whole
inferential machinery is set and the computation of estimators is
usually automatically derived from this setup. Obviously, the
practical or numerical derivation of these procedures may be
exceedingly difficult or even impossible, as we will see in a few
selected examples. Before, we proceed with an incomplete typology of
the categories and difficulties met by Bayesian inference. First, let
us point out that computational difficulties may originate from one or
several of the following items:
- (1)
- use of a complex parameter space, as for instance in constrained
parameter
sets like those resulting from imposing stationarity constraints in
dynamic models;
- (2)
- use of a complex sampling model with an intractable likelihood, as
for instance in missing data and graphical models;
- (3)
- use of a huge dataset;
- (4)
- use of a complex prior distribution (which may be the posterior
distribution associated with an earlier sample);
- (5)
- use of a complex inferential procedure.
11.2.1 Bayesian Point Estimation
In a formalised representation of Bayesian inference, the statistician
is given (or she selects) a triplet
Using 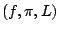 and an observation
and an observation 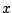 , the Bayesian
inference is always given as the solution to the minimisation
programme
, the Bayesian
inference is always given as the solution to the minimisation
programme
equivalent to the minimisation programme
The corresponding procedure is thus associated, for every 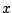 , to the
solution of the above programme (see, e.g. [35],
Chap. 2).
, to the
solution of the above programme (see, e.g. [35],
Chap. 2).
There are therefore two levels of computational difficulties with this
resolution: first the above integral must be computed. Second, it must
be minimised in 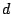 . For the most standard losses, like the squared
error loss,
. For the most standard losses, like the squared
error loss,
the solution to the minimisation problem is universally11.1 known. For instance,
for the squared error loss, it is the posterior mean,
which still requires the computation of both integrals and thus whose
complexity depends on the complexity of both
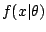 and
and
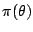 .
.
Example 1
For a normal distribution
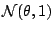 , the use of
a so-called conjugate prior (see, e.g., [35], Chap. 3)
leads to a closed form expression for the mean, since
On the other hand, if we use instead a more involved prior
distribution like a poly-
, the use of
a so-called conjugate prior (see, e.g., [35], Chap. 3)
leads to a closed form expression for the mean, since
On the other hand, if we use instead a more involved prior
distribution like a poly-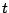 distribution ([5]),
the above integrals cannot be computed in closed form anymore. This is
not a toy example in that the problem may occur after
a sequence of
distribution ([5]),
the above integrals cannot be computed in closed form anymore. This is
not a toy example in that the problem may occur after
a sequence of 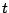 observations, or with a sequence of normal
observations whose variance is unknown.
observations, or with a sequence of normal
observations whose variance is unknown.
The above example is one-dimensional, but, obviously, bigger
challenges await the Bayesian statistician when she wants to tackle
high-dimensional problems.
A related, although conceptually different, inferential issue
concentrates upon prediction,
that is, the approximation of a distribution related with the
parameter of interest, say
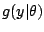 , based on the observation of
, based on the observation of
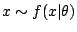 . The predictive distribution is then
defined as
. The predictive distribution is then
defined as
A first difference with the standard point estimation perspective is
obviously that the parameter 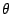 vanishes through the
integration. A second and more profound difference is that this
parameter is not necessarily well-defined anymore. As will become
clearer in a following section, this is a paramount feature in setups
where the model is not well-defined and where the statistician
hesitates between several (or even an infinity of) models. It is also
a case where the standard notion of identifiability
is irrelevant, which paradoxically is a ''plus'' from the
computational point of view, as seen below in, e.g.,
Example 14.
vanishes through the
integration. A second and more profound difference is that this
parameter is not necessarily well-defined anymore. As will become
clearer in a following section, this is a paramount feature in setups
where the model is not well-defined and where the statistician
hesitates between several (or even an infinity of) models. It is also
a case where the standard notion of identifiability
is irrelevant, which paradoxically is a ''plus'' from the
computational point of view, as seen below in, e.g.,
Example 14.
Example 3
Recall that an 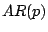 model is given as the
auto-regressive representation of a time series,
It is often the case that the order
model is given as the
auto-regressive representation of a time series,
It is often the case that the order 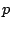 of the
of the 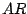 model is not fixed
a priori, but has to be determined from the data
itself. Several models are then competing for the ''best'' fit of
the data, but if the prediction of the
next value
model is not fixed
a priori, but has to be determined from the data
itself. Several models are then competing for the ''best'' fit of
the data, but if the prediction of the
next value 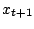 is the most important part of the inference, the
order
is the most important part of the inference, the
order
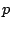 chosen for the best fit is not really relevant. Therefore, all
models can be considered in parallel and aggregated through the
predictive distribution
which thus amounts to integrating over the parameters of all models,
simultaneously:
Note the multiple layers of complexity in this case:
chosen for the best fit is not really relevant. Therefore, all
models can be considered in parallel and aggregated through the
predictive distribution
which thus amounts to integrating over the parameters of all models,
simultaneously:
Note the multiple layers of complexity in this case:
- (1)
- if the prior distribution on
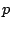 has an infinite support, the
integral simultaneously considers an infinity of models, with parameters of
unbounded dimensions;
has an infinite support, the
integral simultaneously considers an infinity of models, with parameters of
unbounded dimensions;
- (2)
- the parameter
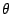 varies from model
varies from model 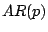 to model
to model
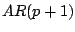 , so must be evaluated differently from one model to another. In
particular, if the stationarity constraint usually imposed in these models is
taken into account, the constraint on
, so must be evaluated differently from one model to another. In
particular, if the stationarity constraint usually imposed in these models is
taken into account, the constraint on
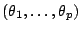 varies11.2 between model
varies11.2 between model 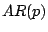 and model
and model
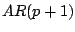 ;
;
- (3)
- prediction is usually used sequentially: every
tick/second/hour/day, the next value is predicted based on the past
values (
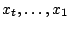 ). Therefore when
). Therefore when 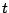 moves to
moves to 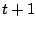 , the entire
posterior distribution
, the entire
posterior distribution
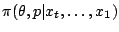 must be re-evaluated
again, possibly with a very tight time constraint as for instance in financial
or radar applications.
must be re-evaluated
again, possibly with a very tight time constraint as for instance in financial
or radar applications.
We will discuss this important problem in deeper details after the
testing section, as part of the model selection problematic.
11.2.2 Testing Hypotheses
A domain where both the philosophy and the implementation of Bayesian
inference are at complete odds with the classical approach is the area
of testing of hypotheses. At a primary level, this is obvious when
opposing the Bayesian evaluation of an hypothesis
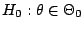
Pr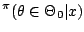 |
|
with a Neyman-Pearson 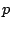 -value
-value
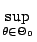 Pr Pr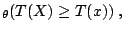 |
|
where 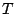 is an appropriate statistic, with observed value
is an appropriate statistic, with observed value 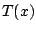 . The
first quantity involves an integral over the parameter space,
while the second provides an evaluation over the
observational space. At a secondary level, the two answers
may also strongly disagree even when the number of observations goes
to infinity, although there exist cases and priors for which they
agree to the order
O
. The
first quantity involves an integral over the parameter space,
while the second provides an evaluation over the
observational space. At a secondary level, the two answers
may also strongly disagree even when the number of observations goes
to infinity, although there exist cases and priors for which they
agree to the order
O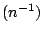 or even
O
or even
O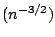 .
(See [35], Sect. 3.5.5 and Chap. 5, for more details.)
.
(See [35], Sect. 3.5.5 and Chap. 5, for more details.)
From a computational point of view, most Bayesian evaluations involve
marginal distributions
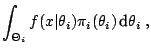 |
(11.1) |
where 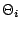 and
and 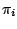 denote the parameter space and the
corresponding prior, respectively, under hypothesis
denote the parameter space and the
corresponding prior, respectively, under hypothesis 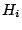
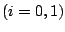 . For instance, the Bayes factor
is defined as the ratio
of the posterior probabilities of the null and the alternative
hypotheses over the ratio of the prior probabilities of the null and
the alternative hypotheses, i.e.,
. For instance, the Bayes factor
is defined as the ratio
of the posterior probabilities of the null and the alternative
hypotheses over the ratio of the prior probabilities of the null and
the alternative hypotheses, i.e.,
This quantity is instrumental in the computation of the posterior
probability
under equal prior probabilities for both 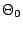 and
and 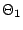 . It
is also the central tool in practical (as opposed to decisional)
Bayesian testing ([26]) as the Bayesian equivalent of
the likelihood ratio.
. It
is also the central tool in practical (as opposed to decisional)
Bayesian testing ([26]) as the Bayesian equivalent of
the likelihood ratio.
The first ratio in
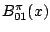 is then the ratio of integrals of
the form (11.1) and it is rather common to face difficulties
in the computation of both integrals.11.3
is then the ratio of integrals of
the form (11.1) and it is rather common to face difficulties
in the computation of both integrals.11.3
In a related manner, confidence regions are also mostly
intractable, being defined through the solution to an implicit
equation. Indeed, the Bayesian confidence region for
a parameter 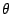 is defined as the highest posterior
region,
is defined as the highest posterior
region,
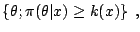 |
(11.2) |
where 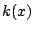 is determined by the coverage constraint
is determined by the coverage constraint
Pr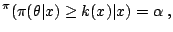 |
|
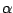 being the confidence level. While the normalising constant is
not necessary to construct a confidence region, the resolution of the
implicit equation (11.2) is rarely straightforward!
being the confidence level. While the normalising constant is
not necessary to construct a confidence region, the resolution of the
implicit equation (11.2) is rarely straightforward!
Example 5
Consider a binomial observation
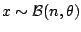 with
a conjugate prior distribution,
with
a conjugate prior distribution,
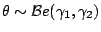 . In this case, the
posterior distribution is available in closed form,
However, the determination of the
. In this case, the
posterior distribution is available in closed form,
However, the determination of the 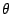 's such that
with
's such that
with
Pr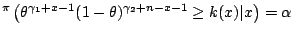 |
|
is not possible analytically. It actually implies two levels of
numerical difficulties:
- Step 1
- find the solution(s) to
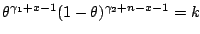 ,
,
- Step 2
- find the
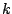 corresponding to the right coverage,
corresponding to the right coverage,
and each value of 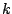 examined in Step 2. requires a new resolution of
Step 1.
examined in Step 2. requires a new resolution of
Step 1.
The setting is usually much more complex when 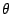 is
a multidimensional parameter, because the interest is usually in
getting marginal confidence sets. Example 2 is an
illustration of this setting: deriving a confidence region on one
component,
is
a multidimensional parameter, because the interest is usually in
getting marginal confidence sets. Example 2 is an
illustration of this setting: deriving a confidence region on one
component, 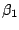 say, first involves computing the marginal
posterior distribution of this component. As in Example 4,
the integral
say, first involves computing the marginal
posterior distribution of this component. As in Example 4,
the integral
which is proportional to
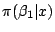 , is most often intractable.
, is most often intractable.
11.2.3 Model Choice
We distinguish model choice
from testing, not only because it leads to further computational
difficulties, but also because it encompasses a larger scope of
inferential goals than mere testing. Note first that model choice has
been the subject of considerable effort in the past years, and has
seen many advances, including the coverage of problems of higher
complexity and the introduction of new concepts. We stress that such
advances mostly owe to the introduction of new computational methods.
As discussed in further details in Robert (2001, Chap. 7), the
inferential action related with model choice does take place on
a wider scale: it covers and compares models, rather than parameters,
which makes the sampling distribution 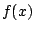 ''more unknown'' than
simply depending on an undetermined parameter. In some respect, it is
thus closer to estimation than to regular testing.
In any case, it requires a more precise evaluation of the consequences
of choosing the ''wrong'' model or, equivalently of deciding which
model is the most appropriate to the data at hand. It is thus both
broader and less definitive as deciding whether
''more unknown'' than
simply depending on an undetermined parameter. In some respect, it is
thus closer to estimation than to regular testing.
In any case, it requires a more precise evaluation of the consequences
of choosing the ''wrong'' model or, equivalently of deciding which
model is the most appropriate to the data at hand. It is thus both
broader and less definitive as deciding whether
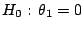 is
true. At last, the larger inferential scope mentioned in the first
point means that we are leaving for a while the well-charted domain of
solid parametric models.
is
true. At last, the larger inferential scope mentioned in the first
point means that we are leaving for a while the well-charted domain of
solid parametric models.
From a computational point of view, model choice involves more complex
structures that, almost systematically, require advanced tools, like
simulation methods which can handle collections of parameter spaces
(also called spaces of varying dimensions),
specially designed for model comparison.
Example 6
A mixture of distributions is the representation of
a distribution (density) as the weighted sum of standard distributions
(densities). For instance, a mixture of Poisson distributions, denoted as
has the following density:
Pr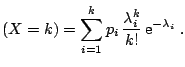 |
|
This representation of distributions is multi-faceted and can be used
in populations with known heterogeneities (in which case a component
of the mixture corresponds to an homogeneous part of the population)
as well as a non-parametric modelling of unknown populations. This
means that, in some cases, 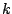 is known and, in others, it is both
unknown and part of the inferential problem.
is known and, in others, it is both
unknown and part of the inferential problem.
First, consider the setting where several (parametric) models are in
competition,
the index set 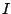 being possibly infinite. From a Bayesian point of
view, a prior distribution must be constructed for each model
being possibly infinite. From a Bayesian point of
view, a prior distribution must be constructed for each model
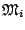 as if it were the only and true model under
consideration since, in most perspectives except model
averaging,
one of these models will be selected and used as the only and
true model. The parameter space
associated with the above set of models can be written as
as if it were the only and true model under
consideration since, in most perspectives except model
averaging,
one of these models will be selected and used as the only and
true model. The parameter space
associated with the above set of models can be written as
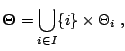 |
(11.3) |
the model indicator 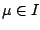 being now part of the parameters. So,
if the statistician allocates probabilities
being now part of the parameters. So,
if the statistician allocates probabilities 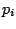 to the indicator
values, that is, to the models
to the indicator
values, that is, to the models
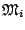
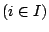 , and if
she then defines priors
, and if
she then defines priors
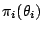 on the parameter subspaces
on the parameter subspaces
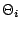 , things fold over by virtue of Bayes's theorem,
as usual, since she can compute
, things fold over by virtue of Bayes's theorem,
as usual, since she can compute
While a common solution based on this prior modeling is simply to take
the (marginal) MAP estimator
of 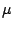 , that is, to determine the model with the largest
, that is, to determine the model with the largest
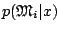 , or even to use directly the average
, or even to use directly the average
as a predictive density in 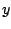 in model averaging,
a deeper-decision theoretic evaluation is often necessary.
in model averaging,
a deeper-decision theoretic evaluation is often necessary.
As stressed earlier in this section, the computation of predictive
densities, marginals, Bayes factors,
and other quantities related to the model choice procedures is
generally very involved, with specificities that call for tailor-made
solutions:
- The computation of integrals is increased by a factor corresponding to
the number of models under consideration.
- Some parameter spaces are infinite-dimensional, as in non-parametric
settings and that may cause measure-theoretic complications.
- The computation of posterior or predictive quantities involves
integration over different parameter spaces and thus increases the
computational burden, since there is no time savings from one subspace to the
next.
- In some settings, the size of the collection of models is very large or
even infinite and
some models cannot be explored. For instance, in
Example 4, the collection of all submodels is of size
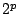 and some pruning method must be found in variable selection to
avoid exploring the whole tree of all submodels.
and some pruning method must be found in variable selection to
avoid exploring the whole tree of all submodels.




Next: 11.3 Monte Carlo Methods
Up: 11. Bayesian Computational Methods
Previous: 11.1 Introduction
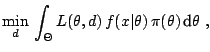
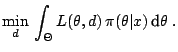
![]() . For the most standard losses, like the squared
error loss,
. For the most standard losses, like the squared
error loss,
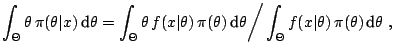
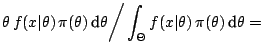
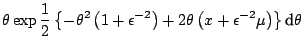
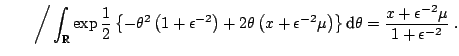
![$\displaystyle \pi(\theta) = \prod_{i=1}^k \left[ \alpha_i+(\theta-\beta_i)^2 \right]^{-\nu_i} \qquad \alpha,\nu>0$](img6107.gif)
![]() , based on the observation of
, based on the observation of
![]() . The predictive distribution is then
defined as
. The predictive distribution is then
defined as
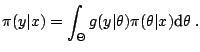
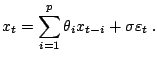
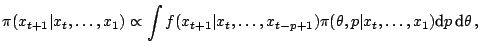
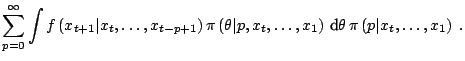
![]()
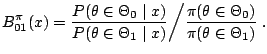
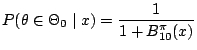
![]() is then the ratio of integrals of
the form (11.1) and it is rather common to face difficulties
in the computation of both integrals.11.3
is then the ratio of integrals of
the form (11.1) and it is rather common to face difficulties
in the computation of both integrals.11.3
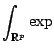
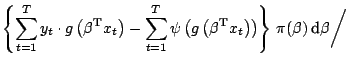
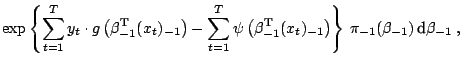
![]() is defined as the highest posterior
region,
is defined as the highest posterior
region,
![]() is
a multidimensional parameter, because the interest is usually in
getting marginal confidence sets. Example 2 is an
illustration of this setting: deriving a confidence region on one
component,
is
a multidimensional parameter, because the interest is usually in
getting marginal confidence sets. Example 2 is an
illustration of this setting: deriving a confidence region on one
component, ![]() say, first involves computing the marginal
posterior distribution of this component. As in Example 4,
the integral
say, first involves computing the marginal
posterior distribution of this component. As in Example 4,
the integral
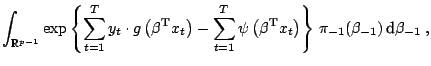
![]() ''more unknown'' than
simply depending on an undetermined parameter. In some respect, it is
thus closer to estimation than to regular testing.
In any case, it requires a more precise evaluation of the consequences
of choosing the ''wrong'' model or, equivalently of deciding which
model is the most appropriate to the data at hand. It is thus both
broader and less definitive as deciding whether
''more unknown'' than
simply depending on an undetermined parameter. In some respect, it is
thus closer to estimation than to regular testing.
In any case, it requires a more precise evaluation of the consequences
of choosing the ''wrong'' model or, equivalently of deciding which
model is the most appropriate to the data at hand. It is thus both
broader and less definitive as deciding whether
![]() is
true. At last, the larger inferential scope mentioned in the first
point means that we are leaving for a while the well-charted domain of
solid parametric models.
is
true. At last, the larger inferential scope mentioned in the first
point means that we are leaving for a while the well-charted domain of
solid parametric models.