![\includegraphics[width=11.7cm]{text/3-11/adap.eps}](img6409.gif) |
While MCMC algorithms considerably expanded the range of applications of Bayesian analysis, they are not, by any means, the end of the story! Further developments are taking place, either at the fringe of the MCMC realm or far away from it. We indicate below a few of the directions in Bayesian computational Statistics, omitting many more that also are of interest...
Given the range of situations where MCMC applies, it is unrealistic to hope for a generic MCMC sampler that would function in every possible setting. The more generic proposals like random-walk Metropolis-Hastings algorithms are known to fail in large dimension and disconnected supports, because they take too long to explore the space of interest ([31]). The reason for this impossibility theorem is that, in realistic problems, the complexity of the distribution to simulation is the very reason why MCMC is used! So it is difficult to ask for a prior opinion about this distribution, its support or the parameters of the proposal distribution used in the MCMC algorithm: intuition is close to void in most of these problems.
However, the performances of off-the-shelve algorithms like the random-walk Metropolis-Hastings scheme bring information about the distribution of interest and, as such, should be incorporated in the design of better and more powerful algorithms. The problem is that we usually miss the time to train the algorithm on these previous performances and are looking for the Holy Grail of automated MCMC procedures! While it is natural to think that the information brought by the first steps of an MCMC algorithm should be used in later steps, there is a severe catch: using the whole past of the ''chain'' implies that this is not a Markov chain any longer. Therefore, usual convergence theorems do not apply and the validity of the corresponding algorithms is questionable. Further, it may be that, in practice, such algorithms do degenerate to point masses because of a too rapid decrease in the variation of their proposal.
![\includegraphics[width=11.7cm]{text/3-11/adap.eps}](img6409.gif) |
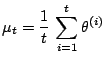 and and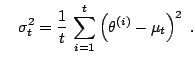 |
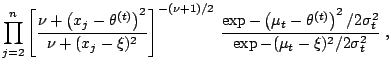 |
![\includegraphics[width=8.7cm]{text/3-11/adap25.eps}](img6414.gif)
|
Even though the Markov chain is converging in distribution to the target distribution (when using a proper, i.e. time-homogeneous updating scheme), using past simulations to create a non-parametric approximation to the target distribution does not work either. Figure 11.18 shows for instance the output of an adaptive scheme in the setting of Example 19 when the proposal distribution is the Gaussian kernel based on earlier simulations. A very large number of iterations is not sufficient to reach an acceptable approximation of the target distribution.
![\includegraphics[width=10cm]{text/3-11/nopada.eps}](img6415.gif)
|
The overall message is thus that one should not constantly
adapt the proposal distribution on the past performances of the
simulated chain. Either the adaptation must cease after a period of
burnin (not to be taken into account for the computations of
expectations and quantities related to the target distribution), or
the adaptive scheme must be theoretically assess on its own
right. This later path is not easy and only a few examples can be
found (so far) in the literature. See, e.g.,
[17] who use regeneration to create block
independence and preserve Markovianity on the paths rather than on the
values, Haario
et al. ([22],[23])
who derive a proper adaptation scheme in the spirit of
Example 19 by using a ridge-like correction to the
empirical variance, and [4] who propose a more
general framework of valid adaptivity based on stochastic optimisation
and the Robbin-Monro algorithm. (The latter actually embeds the chain
of interest
![]() in a larger chain
in a larger chain
![]() that also includes the
parameter of the proposal distribution as well as the gradient of
a performance criterion.)
that also includes the
parameter of the proposal distribution as well as the gradient of
a performance criterion.)
To reach acceptable adaptive algorithms, while avoiding an extended study of their theoretical properties, a better alternative is to leave the structure of Markov chains and to consider sequential or population Monte Carlo methods ([25], [6]) that have much more in common with importance sampling than with MCMC. They are inspired from particle systems that were introduced to handle rapidly changing target distributions like those found in signal processing and imaging ([19,39,13]) but primarily handle fixed but complex target distributions by building a sequence of increasingly better proposal distributions.11.14 Each iteration of the population Monte Carlo (PMC) algorithm thus produces a sample approximately simulated from the target distribution but the iterative structure allows for adaptivity toward the target distribution. Since the validation is based on importance sampling principles, dependence on the past samples can be arbitrary and the approximation to the target is valid (unbiased) at each iteration and does not require convergence times nor stopping rules.
If ![]() indexes the iteration and
indexes the iteration and ![]() the sample point, consider
proposal distributions
the sample point, consider
proposal distributions ![]() that simulate the
that simulate the ![]() 's and
associate to each
's and
associate to each ![]() an importance weight
an importance weight
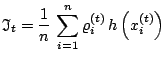 |
![$\displaystyle ~~\,\iint \frac{\pi(x)}{q_{it}(x\vert\zeta)} \, h(x) q_{it}(x) {\...
... x\,g(\zeta) {\text{d}}\zeta = \mathbb{E}^{\pi}[h(X)]\;.%\label{eq:expectadec}
$](img6423.gif) |
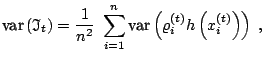 |
Since, usually, the density ![]() is unscaled, we use instead
is unscaled, we use instead
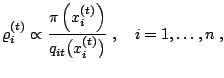 |
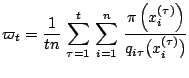 |
Since the above establishes that an simulation scheme based on sample dependent proposals is fundamentally a specific kind of importance sampling, the following algorithm is validated by the same principles as regular importance sampling:
Population Monte Carlo Algorithm
For
![]()
Step (1) is singled out because it is the central property of the PMC
algorithm, namely that adaptivity can be extended to the individual
level and that the ![]() 's can be picked based on the performances
of the previous
's can be picked based on the performances
of the previous
![]() 's or even on all the previously simulated
samples, if storage allows. For instance, the
's or even on all the previously simulated
samples, if storage allows. For instance, the ![]() 's can include
large tails proposals as in the defensive sampling strategy
of [24], to ensure finite variance. Similarly,
Warnes' (2001) non-parametric Gaussian kernel approximation can be
used as a proposal.11.15 (See also
[42] smooth bootstrap as
an earlier example of PMC algorithm.)
's can include
large tails proposals as in the defensive sampling strategy
of [24], to ensure finite variance. Similarly,
Warnes' (2001) non-parametric Gaussian kernel approximation can be
used as a proposal.11.15 (See also
[42] smooth bootstrap as
an earlier example of PMC algorithm.)
The major difference between the PMC algorithm and earlier proposals
in the particle system literature is that past dependent moves as
those of [16] remain within the MCMC framework,
with Markov transition kernels with stationary distribution equal
to ![]() .
.
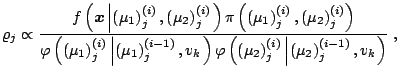 |
Compared with an MCMC algorithm in the same setting (see
Examples 15 and 16), the main feature of this
algorithm is its ability to deal with multiscale proposals in an
unsupervised manner. The upper row of Fig. 11.21 produces
the frequencies of the five variances ![]() used in the proposals
along iterations: The two largest variances
used in the proposals
along iterations: The two largest variances ![]() most often have
a zero survival rate, but sometimes experience bursts of survival. In
fact, too large a variance mostly produces points that are irrelevant
for the posterior distribution, but once in a while a point
most often have
a zero survival rate, but sometimes experience bursts of survival. In
fact, too large a variance mostly produces points that are irrelevant
for the posterior distribution, but once in a while a point
![]() gets close to one of the modes of the posterior. When
this occurs, the corresponding
gets close to one of the modes of the posterior. When
this occurs, the corresponding ![]() is large and
is large and
![]() is thus heavily resampled. The upper right graph
shows that the other proposals are rather evenly sampled along
iterations. The influence of the variation in the proposals on the
estimation of the means
is thus heavily resampled. The upper right graph
shows that the other proposals are rather evenly sampled along
iterations. The influence of the variation in the proposals on the
estimation of the means ![]() and
and ![]() can be seen on the middle
and lower panels of Fig. 11.21. First, the cumulative
averages quickly stabilize over iterations, by virtue of the general
importance sampling proposal. Second, the corresponding variances
take longer to stabilize but this is to be expected, given the regular
reappearance of subsamples with large variances.
can be seen on the middle
and lower panels of Fig. 11.21. First, the cumulative
averages quickly stabilize over iterations, by virtue of the general
importance sampling proposal. Second, the corresponding variances
take longer to stabilize but this is to be expected, given the regular
reappearance of subsamples with large variances.
In comparison with Figs. 11.10 and 11.11, Fig. 11.19 shows that the sample produced by the PMC algorithm is quite in agreement with the modal zone of the posterior distribution. The second mode, which is much lower, is not preserved in the sample after the first iteration. Figure 11.20 also shows that the weights are quite similar, with no overwhelming weight in the sample.
![\includegraphics[width=10.5cm]{text/3-11/pmc2mix.eps}](img6448.gif)
|
![\includegraphics[width=10.5cm]{text/3-11/hpmc2mix.eps}](img6449.gif)
|
![\includegraphics[width=11cm]{text/3-11/itersamp.eps}](img6451.gif)
|
The generality in the choice of the proposal distributions ![]() is
obviously due to the abandonment of the MCMC
framework.
The difference with an MCMC framework is not simply a theoretical
advantage: as seen in Sect. 11.5.1, proposals based on
the whole past of the chain do not often work. Even algorithms
validated by MCMC steps may have difficulties: in one example of
[6], a Metropolis-Hastings scheme
does not work well, while a PMC algorithm based on the same proposal
produces correct answers.
is
obviously due to the abandonment of the MCMC
framework.
The difference with an MCMC framework is not simply a theoretical
advantage: as seen in Sect. 11.5.1, proposals based on
the whole past of the chain do not often work. Even algorithms
validated by MCMC steps may have difficulties: in one example of
[6], a Metropolis-Hastings scheme
does not work well, while a PMC algorithm based on the same proposal
produces correct answers.