1.4 Cross-Validation and Generalized Cross-Validation

The reason one cannot use the $\mathrm{GOF}$ for model selection is that it generally under-estimates the generalization error of a model ([16,25]). For example, (1.21) shows that the RSS under-estimates the $\mathrm{PSE}$ by $2\sigma^2 trH(\lambda)/n$. Thus, similar to the correction term in the $\mathrm{AIC}$, the second term in the $\mathrm{C}_p$ criterion corrects this bias. The bias in RSS is a result of using the same data for model fitting and model evaluation. Ideally, these two tasks should be separated using independent samples. This can be achieved by splitting the whole data into two subsamples, a training (calibration) sample for model fitting and a test (validation) sample for model evaluation. This approach, however, is not efficient unless the sample size is large. The idea behind the cross-validation is to recycle data by switching the roles of training and test samples.

Suppose that one has decided on a measure of discrepancy for model evaluation, for example the prediction error. A $V$-fold cross-validation selects a model as follows.

1. Split the whole data into $V$ disjoint subsamples $S_1,\cdots,S_V$.
2. For $v=1,\cdots,V$, fit model $M_\lambda$ to the training sample $\cup_{i \ne v} S_i$, and compute discrepancy, $d_v(\boldsymbol{\lambda})$, using the test sample $S_v$.
3. Find optimal $\lambda$ as the minimizer of the overall discrepancy $d(\boldsymbol{\lambda})=\sum_{v=1}^V d_v(\boldsymbol{\lambda})$.

The cross-validation is a general procedure that can be applied to estimate tuning parameters in a wide variety of problems. To be specific, we now consider the regression model (1.2). For notational simplicity, we consider the delete-1 (leave-one-out) cross-validation with $V=n$. Suppose our objective is prediction. Let $\boldsymbol{y}^{-i}$ be the $n-1$ vector with the $i$th observation, $y_i$, removed from the original response vector $\boldsymbol {y}$. Let $\widehat{f}_{\lambda}^{-i}$ be the estimate based on $n-1$ observations $\boldsymbol{y}^{-i}$. The ordinary cross-validation (OCV) estimate of the prediction error is

$${\mathrm{OCV}}(\lambda)=\frac{1}{n} \sum_{i=1}^n (y_i-\widehat{f}_{\lambda}^{-i}(t_i))^2 \,.$$ (1.24)

A cross-validation estimate of $\lambda$ is the minimizer of (1.24). The cross-validation method was introduced by [3] (also called PRESS) in the context of linear regression and by [52] in the context of smoothing splines. To compute the OCV score, one needs to fit model $M_{\lambda}$ $n$ times, once for each delete-one data $\boldsymbol{y}^{-i}$. This is computationally intensive. Fortunately, a short-cut exists for many situations. Let

$$\notag \tilde{y}_{ij} = \left\{ \begin{array}{ll} y_j, & j \ne i , \\ [2mm] \widehat{f}_{\lambda}^{-i}(t_i), & j=i , \end{array}\right.$$

and $\tilde{\boldsymbol{y}}_i = (\tilde{y}_{i1},\cdots,\tilde{y}_{in})^{\top}$. $\tilde{\boldsymbol{y}}_i$ simply replaces the $i$th element in $\boldsymbol {y}$, the one deleted to get $\boldsymbol{y}^{-i}$, by $\widehat{f}_{\lambda}^{-i}(t_i)$. Let $\tilde{f}_{\lambda}^{-i}$ be the estimate of $f$ with data $\tilde{\boldsymbol{y}}_i$. For many methods such as the trigonometric regression (linear regression in general) and periodic spline (smoothing spline in general), we have the following

Lemma 1 (Leaving-Out-One Lemma)   $\;\tilde{f}_{\lambda}^{-i}(t_i)=\widehat{f}_{\lambda}^{-i}(t_i)$, $~i=1,\cdots,n$.

See [50] and [24] for proofs. Note that even though it is called the leaving-out-one lemma, similar results hold for the leaving-out-of-cluster cross-validation ([55]). See also [56], [59] and [33] for the leaving-out-one lemma for more complicated problems.

For trigonometric regression and periodic spline models, $\widehat{\boldsymbol{f}}_{\lambda} = H(\lambda) \boldsymbol{y}$ for any  $\boldsymbol {y}$. Thus when $\boldsymbol {y}$ is replaced by $\tilde{\boldsymbol{y}}_i$, we have $(\tilde{f}_{\lambda}^{-i}(t_1),\cdots, \tilde{f}_{\lambda}^{-i}(t_n))^{\top}= H(\lambda) \tilde{\boldsymbol{y}}_i$. Denote the elements of $H(\lambda)$ as $h_{ij}, i,j=1,\cdots,n$. Then

$$\widehat{f}_{\lambda}(t_i) = \sum_{j=1}^n h_{ij} y_j,$$

$$\widehat{f}_{\lambda}^{-i}(t_i) = \tilde{f}_{\lambda}^{-i}(t_i) = \sum_{j=1}^n h_{ij} \tilde{y}_j = \sum_{j \ne i} h_{ij} y_j + h_{ii} \widehat{f}_{\lambda}^{-i}(t_i)\,.$$

Combined, we have

$$\notag \widehat{f}_{\lambda}(t_i)-\widehat{f}_{\lambda}^{-i}(t_i)= h_{ii} (y_i-\widehat{f}_{\lambda}^{-i}(t_i))\,.$$

Then it is easy to check that

$$\notag y_i-\widehat{f}_{\lambda}^{-i}(t_i)= (y_i-\widehat{f}_{\lambda}(t_i))/(1-h_{ii})\, ,$$

and the OCV reduces to

$$\mathrm{OCV}(\lambda)=\frac{1}{n} \sum_{i=1}^n \left( \frac{y_i-\widehat{f}_{\lambda}(t_i)}{1-h_{ii}} \right) ^2\, .$$ (1.25)

Thus one only needs to fit the model once with the full data and compute the diagonal elements of the $H(\lambda)$ matrix.

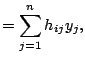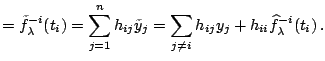Replacing $h_{ii}$ in (1.25) by the average of all diagonal elements, [13] proposed the following generalized cross-validation (GCV) criterion

$$\mathrm{GCV}(\lambda)=\frac{\frac{1}{n} \sum_{i=1}^n ( y_i-\widehat{f}_{\lambda}(t_i))^2} {(1-trH(\lambda)/n)^2}\, .$$ (1.26)

It is easy to see that the GCV criterion is a weighted version of OCV with weights $(1-h_{ii})^2/(1-trH(\lambda)/n)^2$. When $trH(\lambda)/n$ is small, using the approximation $(1-x)^2 \approx 1+2x$,

$$\notag \mathrm{GCV}(\lambda) \approx \frac{1}{n} \sum_{i=1}^n ( y... ...a) \left[ \frac{1}{n} \sum_{i=1}^n ( y_i-\widehat{f}_{\lambda}(t_i))^2 \right].$$

Regarding $\frac{1}{n} \sum_{i=1}^n ( y_i-\widehat{f}_{\lambda}(t_i))^2$ in the second part as an estimate of $\sigma ^2$, the GCV is approximately the same as the $\mathrm{C}_p$ (UBR) criterion. Originally proposed to reduce the computational burden, the GCV criterion has been found to possess several favorable properties ([20,34], [35,36], [50,22]). Sometimes it is difficult to compute each diagonal element in $H(\lambda)$ directly. Nevertheless, it is relatively easy to approximate $trH(\lambda)$ using the randomized trace method ([59]). Thus the GCV criterion may be adopted to many complicated problems ([56,59]). The GCV criterion has non-zero probability to select $\lambda=0$ (interpolation) which may cause problems when the sample size is small. Fortunately, this probability tends to zero exponentially fast as sample size increases ([51]).

For the trigonometric regression,

$$\notag h_{ii} = \frac{1}{n} \left( 1+\sum_{\nu=1}^\lambda 2(\sin^... ...2 2\pi \nu t_i) \right) = \frac{1}{n} (1+2\lambda) = \frac{tr H(\lambda)}{n}\;.$$

For the periodic spline,

$$\notag h_{ii} = \frac{1}{n}+\frac{1}{n} \sum_{\nu=1}^K 2(\sin^2 2... ...u t_i) / (1+\lambda (2\pi \nu)^4) = \frac{tr D}{n} = \frac{tr H(\lambda)}{n}\;.$$

Thus the OCV and GCV are the same for both cases.

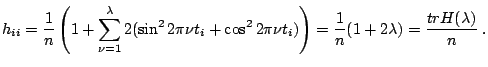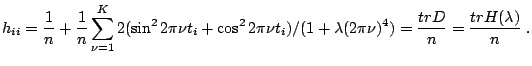Instead of deleting one observation at a time, one may delete $d$ observations at a time as described in the V-fold cross-validation. We will call such a method as delete-d CV. [47] classified various model selection criteria into the following three classes:

Class 1:	$\mathrm{AIC}$, $\mathrm{C}_p$, delete-1 CV and GCV.
Class 2:	Criterion (1.20) with $\theta \rightarrow \infty$ as $n\rightarrow \infty$, and delete-d CV with $d/n \rightarrow 1$.
Class 3:	Criterion (1.20) with a fixed $\theta>2$, and delete-d CV with $d/n \rightarrow \boldsymbol{\tau} \in (0,1)$.

$\mathrm{BIC}$ is a special case of the Class 2. [47] showed that the criteria in Class 1 are asymptotically valid if there is no fixed-dimensional correct model and the criteria in Class 2 are asymptotically valid when the opposite is true. Methods in Class 3 are compromises of those in Classes 1 and 2. Roughly speaking, criteria in the first class would perform better if the true model is ''complex'' and the criteria in the second class would do better if the true model is ''simple''. See also [60] and [46].

The climate data subset was selected by first dividing $365$ days in the year 1990 into $73$ five-day periods, and then selecting measurements on the third day in each period as observations. This is our training sample. Measurements excluding these selected $73$ days may be used as the test sample. This test sample consists $365-73=292$ observations. For the trigonometric model with fixed frequency $\lambda$, we calculate the prediction error using the test sample

$$\mathrm{PE}(\lambda)=\frac{1}{292} \sum_{i=1}^{292} (y_i-\widehat{f}_\lambda(s_i))^2\; ,$$ (1.27)

where $s_i$ are time points for observations in the test sample. The prediction errors are plotted in the left panel of Fig. 1.8 where the minimum is reached at $\lambda=1$. The GCV scores for the trigonometric model is also plotted in the left panel of Fig. 1.8 where the minimum is reached at $\lambda=2$. The GCV score for the periodic spline and the corresponding fits are plotted in the left and right panels of Fig. 1.7 respectively. As expected, the GCV scores are similar to the UBR scores.

Figure 1.8: Left: prediction errors (1.27) (marked as ''v'') and GCV scores (marked as ''c'') for the trigonometric model. Right: the OCV scores in (1.28) on the logarithm scale

As a general methodology, the cross-validation may also be used to select $\theta$ in (1.20) ([43]). Let $\widehat{f}^{-i}_{\widehat{\lambda}^{-i}(\theta)}$ be the estimate based on the delete-one data $\boldsymbol{y}^{-i}$ where $\widehat{\boldsymbol{\lambda}}^{-i}(\theta)$ is selected using (1.20), also based on $\boldsymbol{y}^{-i}$. Then the OCV estimate of prediction error is

$$\mathrm{OCV}(\theta)=\frac{1}{n} \sum_{i=1}^n \left( y_i-\widehat{f}^{-i}_{\widehat{\lambda}^{-i}(\theta)}(t_i)\right)^2\;.$$ (1.28)

The minimum of (1.28) provides an estimate of $\theta$. The OCV score for the trigonometric model is plotted as a function of $\theta$ in the right panel of Fig. 1.8. The minimum is reached at a wide range of $\theta$ values with $\lambda=1$ or $\lambda=2$.