The need for model selection arises when a data-based choice among competing models has to be made. For example, for fitting parametric regression (linear, non-linear and generalized linear) models with multiple independent variables, one needs to decide which variables to include in the model (Chapts. III.7, III.8 and III.12); for fitting non-parametric regression (spline, kernel, local polynomial) models, one needs to decide the amount of smoothing (Chapts. III.5 and III.10); for unsupervised learning, one needs to decide the number of clusters (Chapts. III.13 and III.16); and for tree-based regression and classification, one needs to decide the size of a tree (Chapt. III.14).
Model choice is an integral and critical part of data analysis, an
activity which has become increasingly more important as the ever
increasing computing power makes it possible to fit more realistic,
flexible and complex models. There is a huge literature concerning
this subject ([37,39,10,19])
and we shall restrict this chapter to basic concepts and
principles. We will illustrate these basics using a climate data,
a simulation, and two regression models: parametric trigonometric
regression and non-parametric
periodic splines. We will discuss some commonly used
model selection methods such as Akaike's AIC
([2]), Schwarz's BIC
([45]), Mallow's C![]() ([38]), cross-validation
(CV) ([49]), generalized cross-validation
(GCV)
([13]) and Bayes factors
([31]). We do not intend to
provide a comprehensive review. Readers may find additional
model selection methods in the following chapters.
([38]), cross-validation
(CV) ([49]), generalized cross-validation
(GCV)
([13]) and Bayes factors
([31]). We do not intend to
provide a comprehensive review. Readers may find additional
model selection methods in the following chapters.
Let
![]() be
a collection of candidate models from which one will select
a model for the observed data.
be
a collection of candidate models from which one will select
a model for the observed data. ![]() is the model index
belonging to a set
is the model index
belonging to a set ![]() which may be finite, countable or
uncountable.
which may be finite, countable or
uncountable.
Variable selection in multiple regression is perhaps the most common form of model selection in practice. Consider the following linear model
For illustration, we will use part of a climate data set downloaded
from the Carbon Dioxide Information Analysis Center at
http://cdiac.ornl.gov/ftp/ndp070. The data consists of daily maximum
temperatures and other climatological variables from ![]() stations
across the contiguous United States. We choose daily maximum
temperatures from the station in Charleston, South Carolina, which has
the longest records from 1871 to 1997. We use records in the year 1990
as observations. Records from other years provide information about
the population. To avoid correlation (see
Sect. 1.6) and simplify the presentation, we divided
stations
across the contiguous United States. We choose daily maximum
temperatures from the station in Charleston, South Carolina, which has
the longest records from 1871 to 1997. We use records in the year 1990
as observations. Records from other years provide information about
the population. To avoid correlation (see
Sect. 1.6) and simplify the presentation, we divided
![]() days in 1990 into
days in 1990 into ![]() five-day periods. The measurements on
the third day in each period is selected as observations. Thus the
data we use in our analyses is a subset consisting of every fifth day
records in 1990 and the total number of observations
five-day periods. The measurements on
the third day in each period is selected as observations. Thus the
data we use in our analyses is a subset consisting of every fifth day
records in 1990 and the total number of observations ![]() . For
simplicity, we transform the time variable
. For
simplicity, we transform the time variable ![]() into the interval
into the interval
![]() . The data is shown in the left panel of
Fig. 1.1.
. The data is shown in the left panel of
Fig. 1.1.
![\includegraphics[width=11.7cm]{text/3-1/data.eps}](img3211.gif)
|
Our goal is to investigate how maximum temperature changes over time in a year. Consider a regression model
In the middle panel of Fig. 1.1, we plot observations
on the same selected ![]() days from 1871 to
1997. Assuming model (1.2) is appropriate for all
years, the points represent
days from 1871 to
1997. Assuming model (1.2) is appropriate for all
years, the points represent ![]() realizations from
model (1.2). The averages reflect the true mean
function
realizations from
model (1.2). The averages reflect the true mean
function ![]() and the ranges reflect fluctuations. In the
right panel, a smoothed version of the averages is shown,
together with the observations in 1990. One may imagine that
these observations were generated from the smoothed curve plus
random errors. Our goal is to recover
and the ranges reflect fluctuations. In the
right panel, a smoothed version of the averages is shown,
together with the observations in 1990. One may imagine that
these observations were generated from the smoothed curve plus
random errors. Our goal is to recover ![]() from the noisy
data. Before proceeding to estimation, one needs to decide
a model space for the function
from the noisy
data. Before proceeding to estimation, one needs to decide
a model space for the function ![]() . Intuitively, a larger
space provides greater potential to recover or approximate
. Intuitively, a larger
space provides greater potential to recover or approximate
![]() . At the same time, a larger space makes model
identification and estimation more difficult ([57]).
Thus the greater potential provided by the larger space is
more difficult to reach. One should use as much prior
knowledge as possible to narrow down the choice of model
spaces. Since
. At the same time, a larger space makes model
identification and estimation more difficult ([57]).
Thus the greater potential provided by the larger space is
more difficult to reach. One should use as much prior
knowledge as possible to narrow down the choice of model
spaces. Since ![]() represents mean maximum temperature in
a year, we will assume that
represents mean maximum temperature in
a year, we will assume that ![]() is a periodic function.
is a periodic function.
Trigonometric Regression Model.
It is a common practice to fit the periodic function ![]() using
a trigonometric model up to a certain frequency, say
using
a trigonometric model up to a certain frequency, say
![]() , where
, where
![]() and
and
![]() . Then the model space is
. Then the model space is
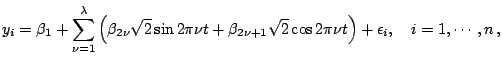 |
(1.4) |
 |
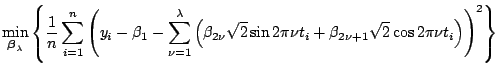 |
(1.5) |
Since design points are equally spaced, we have the following orthogonality relations:
Let
![]() be the estimate of
be the estimate of ![]() where the
dependence on
where the
dependence on ![]() is expressed explicitly. Then the fits
is expressed explicitly. Then the fits
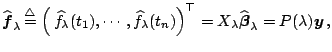 |
| (1.8) |
Fits for several ![]() (labeled as
(labeled as ![]() in strips) are
shown in the top two rows of Fig. 1.2. Obviously as
in strips) are
shown in the top two rows of Fig. 1.2. Obviously as
![]() increases from zero to
increases from zero to ![]() , we have a family of
models ranging from a constant to interpolation. A natural
question is that which model (
, we have a family of
models ranging from a constant to interpolation. A natural
question is that which model (![]() ) gives the ''best''
estimate of
) gives the ''best''
estimate of ![]() .
.
![\includegraphics[width=\textwidth]{text/3-1/fits.eps}](img3257.gif)
|
Periodic Spline.
In addition to the periodicity, it is often reasonable to
assume that ![]() is a smooth function of
is a smooth function of
![]() . Specifically, we assume the following infinite
dimensional space ([50,22])
. Specifically, we assume the following infinite
dimensional space ([50,22])
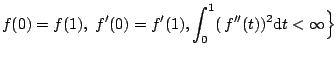 |
(1.9) |
The exact solution to (1.10) can be found in [50]. To simplify the argument, as in [50], we consider the following approximation of the original problem
Let
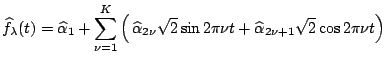 |
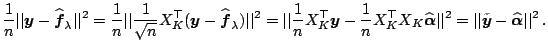 |
Let
![]() . Then
. Then
![]() , and
the fit
, and
the fit
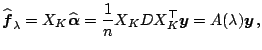 |
| (1.14) |
We choose the trigonometric regression and periodic spline
models for illustration because of their simple model
indexing: the first has a finite set of consecutive integers
![]() and the second has a continuous
interval
and the second has a continuous
interval
![]() .
.
This chapter is organized as follows. In Sect. 1.2, we
discuss the trade-offs between the goodness-of-fit
and model complexity,
and the trade-offs between bias and
variance. We also introduce mean
squared error as a target criterion. In Sect. 1.3, we
introduce some commonly used model selection methods:
AIC, BIC, C![]() ,
AIC
,
AIC![]() and a data-adaptive choice of the
penalty. In Sect. 1.4, we discuss the
cross-validation and the generalized
cross-validation
methods. In Sect. 1.5, we discuss Bayes factor
and its approximations. In
Sect. 1.6, we illustrate potential effects of
heteroscedasticity and correlation on model selection
methods. The chapter ends with some general comments in
Sect. 1.7.
and a data-adaptive choice of the
penalty. In Sect. 1.4, we discuss the
cross-validation and the generalized
cross-validation
methods. In Sect. 1.5, we discuss Bayes factor
and its approximations. In
Sect. 1.6, we illustrate potential effects of
heteroscedasticity and correlation on model selection
methods. The chapter ends with some general comments in
Sect. 1.7.