Subsections

• 8.2.1 Fitting of Nonlinear Regression
  • 8.2.1.1 Newton's Method
  • 8.2.1.2 Gauss-Newton Method
  • 8.2.1.3 Levenberg-Marquardt Method
  
  
• 8.2.2 Statistical Inference
• 8.2.3 Ill-conditioned Nonlinear System

8.2 Nonlinear Regression Modeling

In this section, we study the nonlinear regression model

$$y_i = h(\boldsymbol{x}_{i}, \boldsymbol{\beta}_0) + \varepsilon_{i}\;,$$ (8.16)

$i=1,\ldots,n$, where $h:\mathbb{R}^p\times \mathbb{R}^k \to \mathbb{R}$ is a known regression function and $\boldsymbol{\beta}_0$ is a vector of $k$ unknown parameters. Let us note that the methods discussed in this section are primarily meant for truly nonlinear models rather than intrinsically linear models. A regression model is called intrinsically linear if it can be unambiguously transformed to a model linear in parameters. For example, the regression model $y = \beta_1 x /(\beta_2 + x)$ can be expressed as $1/y = 1/\beta_1 + \beta_2/\beta_1 x$, which is linear in parameters $\theta_1 = 1/\beta_1$ and $\theta_2 = \beta_2/\beta_1$. Transforming a model to its linear form can often provide better inference, such as confidence regions, although one has to be aware of the effects of the transformation on the error-term distribution.

We first discuss the fitting and inference in the nonlinear regression (Sects. 8.2.1 and 8.2.2), whereby we again concentrate on the least square estimation. For an extensive discussion of theory and practice of nonlinear least squares regression see monographs [3], [8] and [80]. Second, similarly to the linear modeling section, methods for ill-conditioned nonlinear systems are briefly reviewed in Sect. 8.2.3.

8.2.1 Fitting of Nonlinear Regression

In this section, we concentrate on estimating the vector $\boldsymbol{\beta}_0$ of unknown parameters in (8.16) by nonlinear least squares.

Definition 8   The nonlinear least squares ( $\mathrm{NLS}$) estimator for the regression model (8.16) is defined by

$$\widehat{\boldsymbol{\beta}}^{\mathrm{NLS}} = \mathop{\mathrm{arg... ...hbb{R}^p} \sum_{i=1}^n \{y_i - h(\boldsymbol{x}_{i}, \boldsymbol{\beta})\}^2\;.$$ (8.17)

Contrary to the linear model fitting, we cannot express analytically the solution of this optimization problem for a general function $h$. On the other hand, we can try to approximate the nonlinear objective function using the Taylor expansion because the existence of the first two derivatives of $h$ is an often used condition for the asymptotic normality of $\mathrm{NLS}$, and thus, could be readily assumed. Denoting $\boldsymbol{h}(\widehat{\boldsymbol{\beta}}) = \{ h(\boldsymbol{x}_{i},\widehat{\boldsymbol{\beta}}) \}_{i=1}^n$ and $S_n(\widehat{\boldsymbol{\beta}}) = \sum_{i=1}^n [y_i - h(\boldsymbol{x}_{i}, \widehat{\boldsymbol{\beta}})]^2$, we can state the following theorem from [4].

Theorem 5   Let $\varepsilon_i$ in (8.16) are independent and identically distributed with $E(\boldsymbol{\varepsilon} \vert \boldsymbol{X}) = 0$ and ${\mathrm{Var}}(\boldsymbol{\varepsilon}\vert\boldsymbol{X}) = \sigma^2 \boldsymbol{I}_{n}$ and let $B$ be an open neighborhood of $\boldsymbol{\beta}_{0}$. Further, assume that $h(\boldsymbol{x}, \boldsymbol{\beta})$ is continuous on $B$ uniformly with respect to $\boldsymbol {x}$ and twice continuously differentiable in $B$ and that

1. $\lim_{n \to \infty} S_n(\boldsymbol{\beta}) \not= 0$ for $\boldsymbol{\beta} \not= \boldsymbol{\beta}_{0}$;
2. $[\partial \boldsymbol{h}(\boldsymbol{\beta}) / \partial \boldsymbol{\beta}_{\t... ...tial \boldsymbol{h}(\boldsymbol{\beta}) / \partial \boldsymbol{\beta}_{\top}]/n$ converges uniformly in B to a finite matrix $\boldsymbol{A}(\boldsymbol{\beta})$, such that $\boldsymbol{A}(\boldsymbol{\beta}_{0})$ is nonsingular;
3. $\boldsymbol{h}(\boldsymbol{\beta}_{1})^{\top} [\partial^2 \boldsymbol{h}(\boldsymbol{\beta}_{2}) / \partial \beta_j \partial \beta_k] / n$ converges uniformly for $\boldsymbol{\beta}_{1}, \boldsymbol{\beta}_{2} \in B$ to a finite matrix for all $j,k=1,\ldots,k$.

Then the $\mathrm{NLS}$ estimator $\widehat{\boldsymbol{\beta}}^{\mathrm{NLS}}$ is consistent and asymptotically normal

$$\sqrt{n} \left( \widehat{\boldsymbol{\beta}}^{\mathrm{NLS}} - \bo... ...t) \to N\left(0, \sigma^2 \boldsymbol{A}(\boldsymbol{\beta}_{0})^{-1}\right)\;.$$ (8.18)

Hence, although there is no general explicit solution to (8.17), we can assume without loss of much generality that the objective function $S_n(\widehat{\boldsymbol{\beta}})$ is twice differentiable in order to devise a numerical optimization algorithm. The second-order Taylor expansion provides then a quadratic approximation of the minimized function, which can be used for obtaining an approximate minimum of the function, see [3]. As a result, one should search in the direction of the steepest descent of a function, which is given by its gradient, to get a better approximation of the minimum. We discuss here the incarnations of these methods specifically for the case of quadratic loss function in (8.17).

8.2.1.1 Newton's Method

The classical method based on the gradient approach is Newton's method, see [54] and [3] for detailed discussion. Starting from an initial point $\widehat{\boldsymbol{\beta}}^{1}$, a better approximation is found by taking

$$\widehat{\boldsymbol{\beta}}^{k+1} = \widehat{\boldsymbol{\beta}}^{k} - \boldsymbol{H}^{-1}\left(\bo... ...\boldsymbol{J}\left(\boldsymbol{r}, \widehat{\boldsymbol{\beta}}^{k}\right) ={}$$ (8.19)

$$= \widehat{\boldsymbol{\beta}}^{k} - \left[\boldsymbol{J}\left(\b... ...k}\right)^{\top} \boldsymbol{r}\left(\widehat{\boldsymbol{\beta}}^{k}\right)\;,$$

where $\boldsymbol{r}(\boldsymbol{\beta}) = \{ [y_i - h(x_i,\boldsymbol{\beta})] \}_{i=1}^n$ represents the vector of residuals, $\boldsymbol{J}(\boldsymbol{f},\boldsymbol{\beta}) = \partial \boldsymbol{f}(\boldsymbol{\beta}) / \partial \boldsymbol{\beta}_{\top}$ is the Jacobian matrix of a vector function $\boldsymbol{f}(\boldsymbol{\beta})$, and $\boldsymbol{H}(\boldsymbol{f},\boldsymbol{\beta}) = \partial^2 \{ \sum_{i=1}^n \boldsymbol{f}_i(\boldsymbol{\beta}) \}$ $/ \partial \boldsymbol{\beta} \partial \boldsymbol{\beta}_{\top}$ is the Hessian matrix of the sum of $\boldsymbol{f}(\boldsymbol{\beta})$.

To find $\widehat{\boldsymbol{\beta}}^{\mathrm{NLS}}$, (8.19) is iterated until convergence is achieved. This is often verified by checking whether the relative change from $\widehat{\boldsymbol{\beta}}^{k}$ to $\widehat{\boldsymbol{\beta}}^{k+1}$ is sufficiently small. Unfortunately, this criterion can indicate a lack of progress rather than convergence. Instead, [8] proposed to check convergence by looking at some measure of orthogonality of residuals $\boldsymbol{r}(\widehat{\boldsymbol{\beta}}^{k})$ towards the regression surface given by $\boldsymbol{h}(\widehat{\boldsymbol{\beta}}^{k})$, since the identification assumption of model (8.16) is $E(\boldsymbol{r}(\boldsymbol{\beta}_0) \vert \boldsymbol{X}) = 0$. See [13], [54] and [92] for more details and further modifications.

To evaluate iteration (8.19), it is necessary to invert the Hessian matrix $\boldsymbol{H}(\boldsymbol{r}^2,\boldsymbol{\beta})$. From the computational point of view, all issues discussed in Sect. 8.1 apply here too and one should use a numerically stable procedure, such as QR or SVD decompositions, to perform the inversion. Moreover, to guarantee that (8.19) leads to a better approximation of the minimum, that is $\boldsymbol{r}(\widehat{\boldsymbol{\beta}}^{k+1})^{\top}\boldsymbol{r}(\wideh... ...\boldsymbol{\beta}}^{k})^{\top}\boldsymbol{r}(\widehat{\boldsymbol{\beta}}^{k})$, the Hessian matrix $\boldsymbol{H}(\boldsymbol{r}^2,\widehat{\boldsymbol{\beta}}^{k})$ needs to be positive definite, which in general holds only in a neighborhood of $\boldsymbol{\beta}_{0}$ (see the Levenberg-Marquardt method for a remedy). Even if it is so, the step in the gradient direction should not be too long, otherwise we ''overshoot.'' Modified Newton's method addresses this by using some fraction $\alpha_{k+1}$ of iteration step $\widehat{\boldsymbol{\beta}}^{k+1} = \widehat{\boldsymbol{\beta}}^{k} - \alpha... ...l{\beta}}^{k}) \boldsymbol{J}(\boldsymbol{r}, \widehat{\boldsymbol{\beta}}^{k})$. See [12], [31] and [54] for some choices of  $\alpha_{k+1}$.

8.2.1.2 Gauss-Newton Method

The Gauss-Newton method is designed specifically for $\mathrm{NLS}$ by replacing the regression function $h(\boldsymbol{x}_{i},\widehat{\boldsymbol{\beta}})$ in (8.17) by its first-order Taylor expansion. The resulting iteration step is

$$\widehat{\boldsymbol{\beta}}^{k+1} = \widehat{\boldsymbol{\beta}}... ...k}\right)^{\top} \boldsymbol{r}\left(\widehat{\boldsymbol{\beta}}^{k}\right)\;.$$ (8.20)

Being rather similar to Newton's method, it does not require the Hessian matrix $\boldsymbol{H}(\boldsymbol{r}^2,\widehat{\boldsymbol{\beta}}^{k})$, which is ''approximated'' by $\boldsymbol{J}(\boldsymbol{h}, \widehat{\boldsymbol{\beta}}^{k})^{\top} \boldsymbol{J}(\boldsymbol{h}, \widehat{\boldsymbol{\beta}}^{k})$ (both matrices are equal in probability for $n\to\infty$ under assumptions of Theorem 5, see [4]). Because it only approximates the true Hessian matrix, this method belongs to the class of quasi-Newton methods. The issues discussed in the case of Newton's method apply also to the Gauss-Newton method.

8.2.1.3 Levenberg-Marquardt Method

Depending on data and the current approximation $\widehat{\boldsymbol{\beta}}^{k}$ of $\widehat{\boldsymbol{\beta}}^{\mathrm{NLS}}$, the Hessian matrix $\boldsymbol{H}(\widehat{\boldsymbol{\beta}}^{k})$ or its approximations such as $\boldsymbol{J}(\boldsymbol{h}, \widehat{\boldsymbol{\beta}}^{k})^{\top} \boldsymbol{J}(\boldsymbol{h}, \widehat{\boldsymbol{\beta}}^{k})$ can be badly conditioned or not positive definite, which could even result in divergence of Newton's method (or a very slow convergence in the case of modified Newton's method). The Levenberg-Marquardt method addresses the ill-conditioning by choosing the search direction $\boldsymbol{d}_k = \widehat{\boldsymbol{\beta}}^{k+1}-\widehat{\boldsymbol{\beta}}^{k}$ as a solution of

$$\left\{\boldsymbol{J}(\boldsymbol{h}, \widehat{\boldsymbol{\beta}... ...boldsymbol{\beta}}^{k})^{\top} \boldsymbol{r}(\widehat{\boldsymbol{\beta}}^{k})$$ (8.21)

(see [65]). This approach is an analogy of $\mathrm{RR}$ used in linear regression (Sect. 8.1.6). Similarly to $\mathrm{RR}$, the Levenberg-Marquardt method improves conditioning of the Hessian matrix and it limits the length of the innovation vector  $\boldsymbol{d}_k$ compared to the (Gauss-)Newton method. See [54] and [13] for a detailed discussion of this algorithm. There are also algorithms combining both Newton's and the Levenberg-Marquardt approaches by using at each step the method that generates a larger reduction in objective function.

Although Newton's method and its modifications are most frequently used in applications, the fact that they find local minima gives rise to various improvements and alternative methods. They range from simple starting the minimization algorithm from several (randomly chosen) initial points to general global-search optimization methods such as genetic algorithms mentioned in Sect. 8.1.3 and discussed in more details in Chaps. II.5 and II.6.

8.2.2 Statistical Inference

Similarly to linear modeling, the inference in nonlinear regression models is mainly based, besides the estimate $\widehat{\boldsymbol{\beta}}^{\mathrm{NLS}}$ itself, on two quantities: the residual sum of squares $\mathrm{RSS} = \boldsymbol{r}(\widehat{\boldsymbol{\beta}}^{\mathrm{NLS}})^{\top}\boldsymbol{r}(\widehat{\boldsymbol{\beta}}^{\mathrm{NLS}})$ and the (asymptotic) variance of the estimate ${\mathrm{Var}}(\widehat{\boldsymbol{\beta}}^{\mathrm{NLS}}) = \sigma^2 \boldsymbol{A}(\boldsymbol{\beta}_{0})^{-1}$, see (8.18). Here we discuss how to compute these quantities for $\widehat{\boldsymbol{\beta}}^{\mathrm{NLS}}$ and its functions.

$\mathrm{RSS}$ will be typically a by-product of a numerical computation procedure, since it constitutes the minimized function. $\mathrm{RSS}$ also provides an estimate of $\sigma ^2$: $s^2 = \mathrm{RSS} / (n-k)$. The same also holds for the matrix $\boldsymbol{A}(\boldsymbol{\beta}_{0})$, which can be consistently estimated by $\boldsymbol{A}(\widehat{\boldsymbol{\beta}}^{\mathrm{NLS}}) = \boldsymbol{J}(\... ...}}^{k})^{\top} \boldsymbol{J}(\boldsymbol{h}, \widehat{\boldsymbol{\beta}}^{k})$, that is, by the asymptotic representation of the Hessian matrix $\boldsymbol{H}(\boldsymbol{r}^2,\widehat{\boldsymbol{\beta}}^{k})$. This matrix or its approximations are computed at every step of (quasi-)Newton methods for $\mathrm{NLS}$, and thus, it will be readily available after the estimation.

Furthermore, the inference in nonlinear regression models may often involve a nonlinear (vector) function of the estimate $\boldsymbol{f}(\widehat{\boldsymbol{\beta}}^{\mathrm{NLS}})$; for example, when we test a hypothesis (see [3], for a discussion of $\mathrm{NLS}$ hypothesis testing). Contrary to linear functions of estimates, where ${\mathrm{Var}}(\boldsymbol{A}\widehat{\boldsymbol{\beta}}^{\mathrm{NLS}} + \bo... ...top} {\mathrm{Var}}(\widehat{\boldsymbol{\beta}}^{\mathrm{NLS}}) \boldsymbol{A}$, there is no exact expression for ${\mathrm{Var}}[\boldsymbol{f}(\widehat{\boldsymbol{\beta}}^{\mathrm{NLS}})]$ in a general case. Thus, we usually assume the first-order differentiability of $\boldsymbol{f}(\cdot)$ and use the Taylor expansion to approximate this variance. Since

$$\boldsymbol{f}\left(\widehat{\boldsymbol{\beta}}\right) = \boldsy... ...ert \widehat{\boldsymbol{\beta}} - \boldsymbol{\beta}_{0} \right\Vert\right)\;,$$

it follows that the variance can be approximated by

$${\mathrm{Var}}\left[\boldsymbol{f}\left(\widehat{\boldsymbol{\bet... ...t{\boldsymbol{\beta}}^{\mathrm{NLS}}\right) }{ \partial \boldsymbol{\beta} }\;.$$

Hence, having an estimate of ${\mathrm{Var}}(\widehat{\boldsymbol{\beta}}^{\mathrm{NLS}})$, the Jacobian matrix $\partial \boldsymbol{f}/\partial \beta^{\top}$ of
function  $\boldsymbol{f}$ evaluated at $\widehat{\boldsymbol{\beta}}^{\mathrm{NLS}}$ provides the first-order approximation of the variance of $\boldsymbol{f}(\widehat{\boldsymbol{\beta}}^{\mathrm{NLS}})$.

8.2.3 Ill-conditioned Nonlinear System

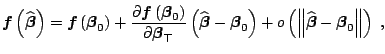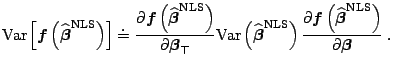Similarly to linear modeling, the nonlinear models can also be ill-conditioned when the Hessian matrix $H(\boldsymbol{r}^2,\widehat{\boldsymbol{\beta}})$ is nearly singular or does not even have a full rank, see Sect. 8.1.2. This can be caused either by the nonlinear regression function $h$ itself or by too many explanatory variables relative to sample size $n$. Here we mention extensions of methods dealing with ill-conditioned problems in the case of linear models (discussed in Sects. 8.1.5-8.1.9) to nonlinear modeling: ridge regression, Stein-rule estimator, Lasso, and partial least squares.

First, one of early nonlinear $\mathrm{RR}$ was proposed by [21], who simply added a diagonal matrix to $\boldsymbol{H}(\boldsymbol{r}^2,\boldsymbol{\beta})$ in (8.19). Since the nonlinear modeling is done by minimizing of an objective function, a more straightforward way is to use the alternative formulation (8.11) of $\mathrm{RR}$ and to minimize

$$\sum_{i=1}^n \left\{y_i - h\left(\boldsymbol{x}_{i}^{\top}, \bold... ...ol{r}\left(\boldsymbol{\beta}\right) + k \Vert \boldsymbol{\beta} \Vert _2^2\;,$$ (8.22)

where $k$ represents the ridge coefficient. See [70] for an application of this approach.

Next, equally straightforward is an application of Stein-rule estimator (8.8) in nonlinear regression, see [56] for a recent study of positive-part Stein-rule estimator within the Box-Cox model. The same could possibly apply to Lasso-type estimators discussed in Sect. 8.1.8 as well: the Euclidian norm $\Vert\boldsymbol{\beta}\Vert _2^2$ in (8.22) would just have to be replaced by another $L_q$ norm. Nevertheless, the behavior of Lasso within linear regression has only recently been studied in more details, and to my best knowledge, there are no results on Lasso in nonlinear models yet.

Finally, there is a range of modifications of $\mathrm{PLS}$ designed for nonlinear regression modeling, which either try to make the relationship between dependent and expl variables linear in unknown parameters or deploy an intrinsically nonlinear model. First, the methods using linearization are typically based on approximating a nonlinear relationship by higher-order polynomials (see quadratic $\mathrm{PLS}$ by [107], and INLR approach by [10]) or a piecewise constant approximation (GIFI approach, see [11]). [108] present an overview of these methods. Second, several recent works introduced intrinsic nonlinearity into $\mathrm{PLS}$ modeling. Among most important contributions, there are [77] and [64] modeling the nonlinear relationship using a forward-feed neural network, [106] and [25] transforming predictors by spline functions, and [5] using fuzzy-clustering regression approach.