References

1

Akaike, H. (1974). A new look at the statistical model identification. IEEE Transactions on Automatic Control, 19: 716-723.

2

Akdeniz, F., Yüksel, G., and Wan, A.T.K. (2004). The moments of the operational almost unbiased ridge regression estimator. Applied Mathematics and Computation: in press.

3

Amemiya, T. (1983). Non-linear regression models. In Griliches, Z. and Intriligator, M.D. (eds) Handbook of Econometrics, Volume 1. North-Holland Publishing Company, Amsterdam.

4

Amemiya, T. (1985). Advanced Econometrics. Harvard University Press, Cambridge, USA.

5

Bang, Y.H., Yoo, C.K. and Lee, I-B. (2003). Nonlinear PLS modeling with fuzzy inference system. Chemometrics and Intelligent Laboratory Systems, 64: 137-155.

6

Barlow, J.L. (1993). Numerical aspects of solving linear least squares problems. In Rao, C.R. (ed), Handbook of Statistics, Volume 9. Elsevier, Amsterdam London New York Tokyo.

7

Barros, A.S. and Rutledge, D.N. (1998). Genetic algorithm applied to the selection of principal components. Chemometrics and Intelligent Laboratory Systems, 40: 65-81.

8

Bates, D.M. and Watts, D.G. (1988). Nonlinear Regression Analysis and Its Applications. Wiley, New York, USA.

9

Bedrick, E.J. and Tsai, C-L. (1994). Model Selection for Multivariate Regression in Small Samples. Biometrics, 50: 226-231.

10

Berglund, A. and Wold, S. (1997). INLR, implicit nonlinear latent variable regression. Journal of Chemometrics, 11: 141-156.

11

Berglund, A., Kettaneh, Wold, S., Bendwell, N. and Cameron, D.R. (2001). The GIFI approach to non-linear PLS modelling. Journal of Chemometrics, 15: 321-336.

12

Berndt, E.R., Hall, B.H., Hall, R.E. and Hausman, J.A. (1974). Estimation and Inference in Nonlinear Structural Models. Annals of Econometric and Social Measurement, 3: 653-666

13

Björck, A. (1996). Numerical Methods for Least Squares Problems. SIAM Press, Philadelphia, USA.

14

Björkström, A. and Sundberg, R. (1996). Continuum regression is not always continuous. Journal of Royal Statistical Society B, 58: 703-710.

15

Björkström, A. and Sundberg, R. (1999). A generalized view on continuum regression. Scandinavian Journal of Statistics, 26: 17-30.

16

Brooks, R. and Stone, M. (1990). Continuum regression: cross-validated sequentially constructed prediction embracing ordinary least squares, partial least squares and principal component regression. Journal of Royal Statistical Society B, 52: 237-269.

17

Brooks, R. and Stone, M. (1994). Joint continuum regression for multiple predicants. Journal of American Statistical Association, 89: 1374-1377.

18

Chambers, L. (1998). Practical Handbook of Genetic Algorithms: Complex Coding Systems, Volume III. CRC Press, USA.

19

Chawla, J.S. (1990). A note on ridge regression. Statistics & Probability Letters, 9: 343-345.

20

Coutis, C. (1996). Partial least squares algorithm yields shrinkage estimators. The Annals of Statistics, 24: 816-824.

21

Dagenais, M.G. (1983). Extension of the ridge regression technique to non-linear models with additive errors. Economic Letters, 12: 169-174.

22

Danilov, D. and Magnus, J.R. (2004). On the harm that ignoring pretesting can cause. Journal of Econometrics, in press.

23

Denham, M.C. (1997). Prediction intervals in partial least squares. Journal of Chemometrics, 11: 39-52

24

Depczynski, U., Frost, V.J. and Molt, K. (2000). Genetic algorithms applied to the selection of factors in principal component regression. Analytica Chimica Acta, 420: 217-227.

25

Durand, J-F. and Sabatier, R. (1997). Additive spline for partial least squares regression. Journal of American Statistical Association, 92: 1546-1554.

26

Edwards, D. and Havranek, T. (1987). A fast model selection procedure for large families of models. Journal of American Statistical Association, 82: 205-213.

27

Efron, B., Hastie, T., Johnstone, I. and Tibshirani, R. (2004). Least Angle Regression. Annals of Statistics, 32: in press.

28

Efroymson, M.A. (1960). Multiple regression analysis. In Ralston, A. and Wilf, H.S. (eds), Mathematical Methods for Digital Computers, Vol. 1, Wiley, New York, USA.

29

Faber, N.M., Song, X-H. and Hopke, P.K. (2003). Sample specific standard error of prediction for partial least squares regression. Trends in Analytical Chemistry, 22: 330-334.

30

Farebrother, R.W. (1976). Further results on the mean square error of ridge estimation. Journal of Royal Statistical Society B, 38: 248-250.

31

Fletcher, R. and Powell, M.J.D. (1963). A rapidly convergent descent method for minimization. Computer Journal 6: 163-168.

32

Frank, I.E., Friedman, J.H., Wold, S., Hastie, T. and Mallows, C. (1993). A statistical view of some chemometrics regression tools. Technometrics, 35(2): 109-148.

33

Garthwaite, P.H. (1994). An interpretation of partial least squares. The Journal of American Statistical Association, 89: 122-127.

34

Gentle, J.E. (1998). Numerical Linear Algebra for Applications in Statistics. Springer, New York, USA.

35

Gruber, M.H.J. (1998). Improving efficiency by shrinkage: the James-Stein and ridge regression estimators. Marcel Dekker, Inc., New York, USA.

36

Gunst, R.F. and Mason, R.L. (1980). Regression Analysis and Its Application: a Data-Oriented Approach. Marcel Dekker, Inc., New York, USA.

37

Härdle, W. (1992). Applied Nonparametric Regression. Cambridge University Press, Cambridge, UK.

38

Härdle, W. and Simar, L. (2003). Applied Multivariate Statistical Analysis. Springer, Heidelberg, Germany.

39

Hawkins, D.M. and Yin, X. (2002). A faster algorithm for ridge regression of reduced rank data. Computational Statistics & Data analysis, 40: 253-262.

40

Helland, I.S. (2001). Some theoretical aspects of partial least squares regression. Chemometrics and Intelligent Laboratory Systems, 58: 97-107.

41

Helland, I.S. and Almoy, T. (1994). Comparison of Prediction Methods When Only a Few Components are Relevant. Journal of American Statistical Association, 89: 583-591.

42

Hocking, R.R. (1996). Methods and Applications of Linear Models: Regression and the Analysis of Variance, 2nd Edition. Wiley, New York, USA.

43

Hoerl, A.E. and Kennard, R.W. (1970). Ridge regression: biased estimation of nonorthogonal problems. Technometrics, 12: 55-67.

44

Hoerl, A.E., Kennard, R.W. and Baldwin, K.F. (1975). Ridge regression: some simulations. Communications in Statistics, 4: 105-123.

45

Hughes, A.W. and Maxwell, L.K. (2003). Model selection using AIC in the presence of one-sided information. Journal of Statistical Planning and Inference, 115: 379-411.

46

Hwang, J.T.G. and Nettleton, D. (2003). Principal components regression with data-chosen components and related methods. Technometrics, 45: 70-79.

47

Ibrahim, J.G. and Ming-Hui, C. (1997). Predictive Variable Selection for the Multivariate Linear Model. Biometrics, 53: 465-478.

48

Jiang, W. and Liu, X. (2004). Consistent model selection based on parameter estimates. Journal of Statistical Planning and Inference, 121: 265-283.

49

Jolliffe, I.T. (1982). A note on the use of the principle components in regression. Applied Statistics, 31(3): 300-303.

50

Jong, S. (1993). SIMPLS: An alternative approach to partial least squares regression. Chemometrics and Intelligent Laboratory Systems, 18: 251-263.

51

Jong, S. (1995). PLS shrinks. Journal of Chemometrics, 9: 323-326.

52

Judge, G.G. and Bock, M.E. (1983). Biased estimation. In Griliches, Z. and Intriligator, M.D. (eds), Handbook of Econometrics, Volume 1, North-Holland Publishing Company, Amsterdam.

53

Kadiyala, K. (1984). A class of almost unbiased and efficient estimators of regression coefficients. Economic Letters, 16: 293-296.

54

Kennedy, W. J. and Gentle, J.E. (1980). Statistical Computing. Marcel Dekker, Inc., New York, USA.

55

Kibria, G. (1996). On preliminary test ridge regression estimators for linear restrictions in a regression model with non-normal disturbances. Communications in Statistics, Theory and Methods, 25: 2349-2369.

56

Kim, M. and Hill, R.C. (1995). Shrinkage estimation in nonlinear regression: the Box-Cox transformation. Journal of Econometrics, 66: 1-33.

57

Knight, K. and Fu, W. (2000). Asymptotics for Lasso-type estimators. The Annals of Statistics, 28: 1356-1389.

58

Leardi, R. and Gonzáles, A.L. (1998). Genetic algorithms applied to feature selection in PLS regression: how and when to use them. Chemometrics and Intellingent Laboratory Systems, 41: 195-207.

59

Leamer, E.E. (1983). Model choice and specification analysis. In Griliches, Z. and Intriligator, M.D. (eds), Handbook of Econometrics, Volume 1, North-Holland Publishing Company, Amsterdam.

60

Li, K-C. (1987). Asymptotic optimality for 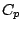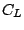$C_p$, $C_L$, cross-validation and generalized cross-validation: discrete index set. Annals of Statistics, 15: 958-975.

61

Li, B., Morris, J. and Martin, E.B. (2002). Model section for partial least squares regression. Chemometrics and Intelligent Laboratory Systems, 64: 79-89.

62

Magnus, J.R. (1999). The traditional pretest estimator. Theory of Probability and Its Applications. 44(2): 293-308.

63

Magnus, J.R. (2002). Estimation of the mean of a univariate normal distribution with known variance. The Econometrics Journal, 5, 225-236.

64

Malthouse, E.C., Tamhane, A.C. and Mah, R.S.H. (1997). Nonlinear partial least squares. Computers in Chemical Engineering, 21(8): 875-890.

65

Marquardt, D.W. (1963). An algorithm for least-squares estimation of nonlinear parameters. Journal of the Society for Industrial and Applied Mathematics, 11: 431-441.

66

McDonald, G.C. and Schwing, R.C. (1973). Instabilities of regression estimates relating air pollution to mortality. Technometrics, 15: 463-482.

67

Miller, A.J. (1984). Selection of Subsets of Regression Variables. Journal of the Royal Statistical Society A, 147(3): 389-425.

68

Miller, A. (2002). Subset Selection in Regression, Chapman & Hall/CRC, USA.

69

Montgomery, D.C., Peck, E.A. and Vining, G.G. (2001). Introduction to Linear Regression Analysis, 3rd Edition, Wiley, New York, USA.

70

Ngo, S.H., Kemény, S. and Deák, A. (2003). Performance of the ridge regression methods as applied to complex linear and nonlinear models. Chemometrics and Intelligent Laboratory Systems, 67: 69-78.

71

Ohtani, K. (1986). On small sample properties of the almost unbiased generalized ridge estimator. Communications in Statistics, Theory and Methods, 22: 2733-2746.

72

Osborne, M.R., Presnell, B. and Turlach, B.A. (1999). On the Lasso and its dual. Journal of Computational and Graphical Statistics, 9: 319-337.

73

Osten, D.W. (1988). Selection of optimal regression models via cross-validation. Journal of Chemometrics, 2: 39-48.

74

Phatak, A., Reilly, P.M. and Pendilis, A. (2002). The asymptotic variance of the univariate PLS estimator. Linear Algera and its Applications, 354: 245-253.

75

Rao, C.R. and Toutenberg, H. (1999). Linear Models, Springer, New York, USA.

76

Rao, C.R. and Wu, Y. (1989). A strongly consistent procedure for model selection in a regression problem. Biometrika, 76: 369-374.

77

Qin, S. and McAvoy, T. (1992). Nonlinear PLS modeling using neural networks. Computers in Chemical Engineering, 16: 379-391.

78

Qin, S.J. (1997). Recursive PLS algorithms for adaptive data modeling. Computers in Chemical Engineering, 22(4): 503-514.

79

Schwarz, G. (1978). Estimating the dimension of a model. The Annals of Statistics, 6: 461-464.

80

Seber, G.A.F. and Wild, C.J. (2003). Nonlinear Regression, Wiley, New York, USA.

81

Shao, J. (1993). Linear model selection by cross-validation. Journal of American Statistical Association, 88: 486-494.

82

Shao, J. (1997). An asymptotic theory for linear model selection. Statistica Sinica, 7: 221-264.

83

Shi, P. and Tsai, C.-L. (1998). A note on the unification of the Akaike information criterion. Journal of the Royal Statistical Society B, 60: 551-558.

84

Shiaishi, T. and Konno, Y. (1995). On construction of improved estimators in multiple-design multivariate linear models under general restrictions. Annals of Institute of Statistical Mathematics, 46: 665-674.

85

Shibata, R. (1981). An optimal selection of regression variables. Biometrika, 68: 45-54.

86

Shibata, R. (1984). Approximate efficiency of a selection procedure for the number of regression variables. Biometrika, 71: 43-49.

87

Singh, R.K., Pandey, S. K. and Srivastava, V.K. (1994). A generalized class of shrinkage estimators in linear regression when disturbances are not normal. Communications in Statistics, Theory and Methods, 23: 2029-2046.

88

Stoica, P. and Söderström, T. (1998). Partial least squares: a first-order analysis. Scandinavian Journal of Statistics, 25: 17-26.

89

Stone, M. (1974). Cross-validatory choice and assessment of statistical predictions. Journal of Royal Statistical Society B, 36: 111-147.

90

Sundberg, R. (1993). Continuum regression and ridge regression. Journal of Royal Statistical Society B, 55: 653-659.

91

Swamy, P.A.V.B., Mehta, J.S. and Rappoport, P.N. (1978). Two methods of evaluating Hoerl and Kennard's ridge regression. Communications in Statistics A, 12: 1133-1155.

92

Thisted, R.A. (1988). Elements of Statistical Computing. Chapman and Hall, London New York.

93

Tibshirani, R. (1996). Regression shrinkage and selection via Lasso. Journal of Royal Statistical Society B, 58: 267-288.

94

Trygg, J. and Wold, S. (2002). Orthogonal projections to latent structures, O-PLS. Journal of Chemometrics, 16(3): 119-128.

95

Ullah, A., Sristava, V.K. and Chandra, R. (1983). Properties of shrinkage estimators in linear regression when disturbances are not normal. Journal of Econometrics, 21: 289-402.

96

Vinod, H.D. and Ullah, A. (1981). Recent Advances in Regression Methods. Marcel Dekker Inc., New York, USA.

97

Wan, A.T.K. (2002). On generalized ridge regression estimators under collinearity and balanced loss. Applies Mathematics and Computation, 129: 455-467.

98

Wang, S.G. and Chow, S.C. (1990). A note on adaptive generalized ridge regression estimator. Statistics & Probability Letters, 10: 17-21.

99

Wang, S.G., Tse, S.K. and Chow, S.C. (1990). On the measures of multicollinearity in least squares regression. Statistics & Probability Letters, 9: 347-355.

100

Wasserman, G.S. and Sudjianto, A. (1994). All subsets regression using a generic search algorithm. Computers and Industrial Engineering, 27: 489-492.

101

Wegelin, J.A. (2000). A survey of partial least squares (PLS) methods, with emphasis on the two-block case. Technical Report 371, Department of Statistics, University of Washington, Seattle.

102

Weiss, R.E. (1995). The influence of variable selection: a bayesian diagnostic perspective. Journal of the American Statistical Association, 90: 619-625.

103

Wentzell, P.D. and Montoto, L.V. (2003). Comparison of principal components regression and partial least squares regression through generic simulations of complex mixtures. Chemometrics and Intelligent Laboratory Systems, 65: 257-279.

104

Wold, H. (1966). Estimation of principle components and related models by iterative least squares. In Krishnaiaah (ed) Multivariate analysis. Academic Press, New York.

105

Wold, S. (1978). Cross-validation estimation of the number of components in factor and principal components analysis. Technometrics, 24: 397-405.

106

Wold, S. (1992). Nonlinear partial least squares modelling II. Spline inner relation. Chemometrics and Intellingent Laboratory Systems, 14: 71-84.

107

Wold, S., Kettaneh-Wold, N. and Skagerberg, B. (1989). Nonlinear PLS modelling. Chemometrics and Intelligent Laboratory Systems, 7: 53-65.

108

Wold, S., Trygg, J., Berglund, A. and Atti, H. (2001). Some recent developments in PLS modeling. Chemometrics and Intelligent Laboratory Systems, 58: 131-150.

109

Zhang, P. (1992). Inference after variable selection in linear regression models. Biometrika, 79(4): 741-746.

110

Zheng, X. and Loh, W-Y. (1995). Consistent variable selection in linear models. Journal of the American Statistical Association, 90: 151-156.