



Next: References
Up: 9. Robust Statistics
Previous: 9.4 Linear Regression
Subsections
9.5 Analysis of Variance
9.5.1 One-way Table
The one-way analysis of variance
is concerned with the comparison of the locations of 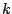 samples
samples
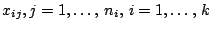 . The term ''analysis of
variance'' goes back
to the pioneering work of
[39]
who decomposed the variance of the combined
samples as follows
. The term ''analysis of
variance'' goes back
to the pioneering work of
[39]
who decomposed the variance of the combined
samples as follows
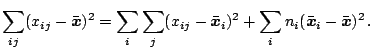 |
(9.121) |
The first term of (9.121) is the total sum of squares, the
second is the sum of squares within samples and the third is the sum
of squares between samples. If the data are modelled as i.i.d. normal
random variables with a common variance 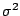 but with the
but with the 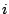 th
sample mean
th
sample mean 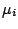 then it is possible to derive a test for the null
hypothesis that the means are equal. The single hypothesis of equal
means is rarely of interest in itself. All pairwise comparisons
then it is possible to derive a test for the null
hypothesis that the means are equal. The single hypothesis of equal
means is rarely of interest in itself. All pairwise comparisons
as well as contrasts
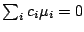 may also be of interest and
give rise to the problem of multiple testing and the associated
difficulties. The use of the
may also be of interest and
give rise to the problem of multiple testing and the associated
difficulties. The use of the 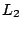 -norm as in (9.121) is
widespread perhaps because of the elegant mathematics. The
peculiarities of data analysis must however have priority over
mathematical theory and as real data sets may contain outliers, be
skewed to some extent and have different scales it becomes clear that
an
-norm as in (9.121) is
widespread perhaps because of the elegant mathematics. The
peculiarities of data analysis must however have priority over
mathematical theory and as real data sets may contain outliers, be
skewed to some extent and have different scales it becomes clear that
an 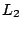 -norm and Gaussian based theory is of limited
applicability. We sketch a robustified approach to the one-way table
(see [28]).
-norm and Gaussian based theory is of limited
applicability. We sketch a robustified approach to the one-way table
(see [28]).
As a first step gross outliers are eliminated from each sample using
a simplified version of the outlier
identification rule based on the median and
MAD of the sample. Using the
robust location and scale functionals 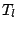 and
and 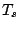 an
an
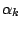 confidence or approximation interval
confidence or approximation interval 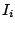 for location
for the
for location
for the 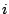 th sample is calculated. To control the error rate for
Gaussian and other samples we set
th sample is calculated. To control the error rate for
Gaussian and other samples we set
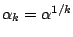 with for
example
with for
example
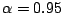 . This choice guarantees that for Gaussian
samples
. This choice guarantees that for Gaussian
samples
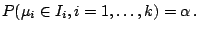 |
(9.122) |
Simulations show that this holds accurately for other symmetric
distributions such as the slash, Cauchy and the double
exponential. All questions relating to the locations of the samples
are now reduced to questions concerning the intervals. For example,
the samples  and
and  can be approximated by the same location value
if and only if
can be approximated by the same location value
if and only if
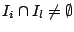 . Similarly if the samples
are in some order derived from a covariable it may be of interest as
to whether the locations can be taken to be non-decreasing. This will
be the case if and only if there exist
. Similarly if the samples
are in some order derived from a covariable it may be of interest as
to whether the locations can be taken to be non-decreasing. This will
be the case if and only if there exist
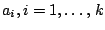 with
with
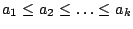 and
and
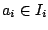 for each
for each 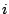 . Because of
(9.122) all such questions when stated in terms of the
. Because of
(9.122) all such questions when stated in terms of the 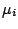 can be tested simultaneously and on Gaussian test beds the error rate
will be
can be tested simultaneously and on Gaussian test beds the error rate
will be 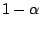 regardless of the number of tests. Another
advantage of the method is that it allows a graphical
representation. Every analysis should include a plot of the boxplots
for the
regardless of the number of tests. Another
advantage of the method is that it allows a graphical
representation. Every analysis should include a plot of the boxplots
for the 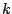 data sets. This can be augmented by the corresponding plot
of the intervals
data sets. This can be augmented by the corresponding plot
of the intervals 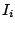 which will often look like the boxplots but if
the sample sizes differ greatly this will influence the lengths of the
intervals but not the form of the boxplots.
which will often look like the boxplots but if
the sample sizes differ greatly this will influence the lengths of the
intervals but not the form of the boxplots.
Given 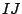 samples
samples
the two-way analysis of variance
in its simplest version looks for a decomposition of the data of the
form
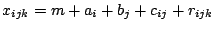 |
(9.123) |
with the the following interpretation. The overall effect is
represented by 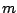 , the row and column effects by the
, the row and column effects by the 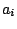 and
and 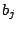 respectively and the interactions by the
respectively and the interactions by the 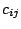 . The
residuals
. The
residuals 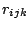 take care of the rest. As it
stands the decomposition (9.123) is not unique but can be
made so by imposing side conditions on the
take care of the rest. As it
stands the decomposition (9.123) is not unique but can be
made so by imposing side conditions on the 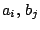 and the
and the
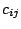 . Typically these are of the form
. Typically these are of the form
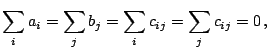 |
(9.124) |
where the latter two hold for all 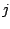 and
and 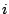 respectively. The
conditions (9.124) are almost always stated as technical
conditions required to make the decomposition (9.123)
identifiable. The impression is given that they are neutral with
respect to any form of data analysis. But this is not the case as
demonstrated by [110] and as can be seen by considering the
restrictions on the interactions
respectively. The
conditions (9.124) are almost always stated as technical
conditions required to make the decomposition (9.123)
identifiable. The impression is given that they are neutral with
respect to any form of data analysis. But this is not the case as
demonstrated by [110] and as can be seen by considering the
restrictions on the interactions 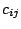 . The minimum number of
interactions for which the restrictions hold is four which, in
particular, excludes the case of a single interaction in one cell. The
restrictions on the row and column effects can also be criticized but
we take this no further than mentioning that the restrictions
. The minimum number of
interactions for which the restrictions hold is four which, in
particular, excludes the case of a single interaction in one cell. The
restrictions on the row and column effects can also be criticized but
we take this no further than mentioning that the restrictions
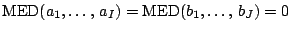 |
(9.125) |
may be more appropriate. The following robustification of the two-way
table is based on [106]. The idea is to look for
a decomposition which minimizes the number of non-zero interactions. We
consider firstly the case of one observation per cell, 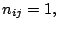 for
all
for
all 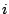 and
and 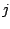 , and look for a decomposition
, and look for a decomposition
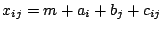 |
(9.126) |
with the smallest number of 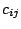 which are non-zero. We denote the
positions of the
which are non-zero. We denote the
positions of the 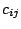 by a
by a 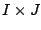 -matrix
-matrix 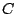 with
with 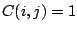 if and only if
if and only if
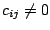 , the remaining entries being zero. It can
be shown that for certain matrices
, the remaining entries being zero. It can
be shown that for certain matrices 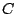 the non-zero interactions
the non-zero interactions
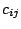 can be recovered whatever their values and, moreover, they
are the unique non-zero residuals of the
can be recovered whatever their values and, moreover, they
are the unique non-zero residuals of the
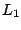 -minimization problem
-minimization problem
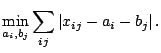 |
(9.127) |
We call matrices 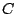 for which this holds unconditionally
identifiable. They can be characterized and two such matrices are
for which this holds unconditionally
identifiable. They can be characterized and two such matrices are
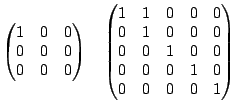 |
(9.128) |
as well as matrices obtained from any permutations of rows and
columns. The above considerations apply to exact models without
noise. It can be shown however that the results hold true if noise is
added in the sense that for unconditionally identifiable matrices
sufficiently large (compared to the noise) interactions 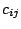 can
be identified as the large residuals from an
can
be identified as the large residuals from an
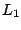 -fit. Three further comments are in order. Firstly Tukey's
median polish can often identify interactions in
the two-way-table. This is because it attempts to approximate the
-fit. Three further comments are in order. Firstly Tukey's
median polish can often identify interactions in
the two-way-table. This is because it attempts to approximate the
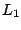 -solution. At each step the
-solution. At each step the 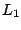 -norm is reduced or at least not
increased but unfortunately the median polish may not converge and,
even if it does, it may not reach the
-norm is reduced or at least not
increased but unfortunately the median polish may not converge and,
even if it does, it may not reach the 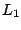 solution. Secondly
solution. Secondly 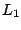 solutions in the presence of noise are not unique. This can be
overcome by approximating the moduls function
solutions in the presence of noise are not unique. This can be
overcome by approximating the moduls function
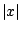 by
a strictly convex function almost linear in the tails. Thirdly, if
there is more than one observation per cell it is recommended that
they are replaced by the median and the method applied
to the medians. Finally we point out that an interaction can also be
an outlier. There is no a priori way of distinguishing
the two.
by
a strictly convex function almost linear in the tails. Thirdly, if
there is more than one observation per cell it is recommended that
they are replaced by the median and the method applied
to the medians. Finally we point out that an interaction can also be
an outlier. There is no a priori way of distinguishing
the two.




Next: References
Up: 9. Robust Statistics
Previous: 9.4 Linear Regression
![]() samples
samples
![]() . The term ''analysis of
variance'' goes back
to the pioneering work of
[39]
who decomposed the variance of the combined
samples as follows
. The term ''analysis of
variance'' goes back
to the pioneering work of
[39]
who decomposed the variance of the combined
samples as follows
![]() and
and ![]() an
an
![]() confidence or approximation interval
confidence or approximation interval ![]() for location
for the
for location
for the ![]() th sample is calculated. To control the error rate for
Gaussian and other samples we set
th sample is calculated. To control the error rate for
Gaussian and other samples we set
![]() with for
example
with for
example
![]() . This choice guarantees that for Gaussian
samples
. This choice guarantees that for Gaussian
samples