The first example involves the real data given in Table 9.1 which are the results of an interlaboratory test. The boxplots are shown in Fig. 9.1 where the dotted line denotes the mean of the observations and the solid line the median.
![\includegraphics[width=83mm,clip]{text/3-9/DaviesGatherFig1.eps}](img5387.gif)
|
We note that only the results of the Laboratories 1 and 3 lie below
the mean whereas all the remaining laboratories return larger
values. In the case of the median, ![]() of the readings
coincide with the median,
of the readings
coincide with the median,
![]() readings are smaller and
readings are smaller and ![]() are larger. A glance at Fig. 9.1 suggests that
in the absence of further information the Laboratories 1 and 3 should
be treated as outliers. This is the course which we
recommend although the issues involved require careful thought. For
the moment we note simply that the median is a robust statistic whereas the mean is not.
are larger. A glance at Fig. 9.1 suggests that
in the absence of further information the Laboratories 1 and 3 should
be treated as outliers. This is the course which we
recommend although the issues involved require careful thought. For
the moment we note simply that the median is a robust statistic whereas the mean is not.
The second example concerns quantifying the scatter of real valued
observations
![]() . This example is partially taken from
[58] and reports a dispute between
[34, p.147] and [38, p.762]
about the relative merits of
. This example is partially taken from
[58] and reports a dispute between
[34, p.147] and [38, p.762]
about the relative merits of
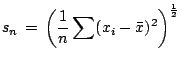 and and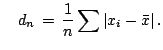 |
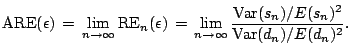 |
thus it becomes painfully clear that the naturally occurring deviations from the idealized model are large enough to render meaningless the traditional asymptotic optimality theory.
The two examples of the previous section illustrate a general
phenomenon. An optimal statistical procedure based on a particular
family of models
![]() can differ considerably from an
optimal procedure based on another family
can differ considerably from an
optimal procedure based on another family
![]() even though
the families
even though
the families
![]() and
and
![]() are very close. This
may be expressed by saying that optimal procedures are often unstable
in that small changes in the data or the model can lead to large
changes in the analysis. The basic philosophy of robust statistics is
to produce statistical procedures which are stable with respect to
small changes in the data or model and even large changes should not
cause a complete breakdown of the procedure.
are very close. This
may be expressed by saying that optimal procedures are often unstable
in that small changes in the data or the model can lead to large
changes in the analysis. The basic philosophy of robust statistics is
to produce statistical procedures which are stable with respect to
small changes in the data or model and even large changes should not
cause a complete breakdown of the procedure.
Any inspection of the data and the removal of aberrant observations
may be regarded as part of robust statistics but it was only with
[78] that the consideration of deviations from
models commenced. He showed that the exact theory based on the normal
distribution for variances is highly nonrobust. There were other
isolated papers on the problem of robustness
([77,6]; Geary (1936, 1937); [44,14,15]).
[108] initiated a wide spread interest in robust statistics which has continued to this day. The
first systematic
investigation of robustness is due to [56] and was expounded in [58]. Huber's approach is functional analytic and he was the first
to investigate the behaviour of a statistical functional over a full
topological neighbourhood of a model instead of restricting the
investigation to other parametric families as in (9.1). Huber
considers three problems. The first is that of
minimizing the bias over certain neighbourhoods and results in the
median as the most robust location functional. For large samples
deviations from the model have consequences which are dominated by the
bias and so this is an important result. The second problem is
concerned with what Tukey calls the statistical version of no free
lunches. If we take the simple model of i.i.d. ![]() observations
then the confidence interval for
observations
then the confidence interval for ![]() based on the mean is on average shorter
than that based on any other statistic. If short confidence intervals
are of interest then one can not only choose the statistic which gives
the shortest interval but also the model itself. The new model must of
course still be consistent with the data but even with this
restriction the confidence interval can be made as small as desired
([26]).
Such a short confidence interval represents a free
lunch and if we do not believe in free lunches then we
must look for that model which maximizes the length of the
confidence interval over a given family of models. If we take all
distributions with variance 1 then the confidence interval for the
based on the mean is on average shorter
than that based on any other statistic. If short confidence intervals
are of interest then one can not only choose the statistic which gives
the shortest interval but also the model itself. The new model must of
course still be consistent with the data but even with this
restriction the confidence interval can be made as small as desired
([26]).
Such a short confidence interval represents a free
lunch and if we do not believe in free lunches then we
must look for that model which maximizes the length of the
confidence interval over a given family of models. If we take all
distributions with variance 1 then the confidence interval for the
![]() distribution is the longest. Huber considers the same problem over
the family
distribution is the longest. Huber considers the same problem over
the family
![]() where
where
![]() denotes the Kolmogoroff metric. Under certain simplifying
assumptions Huber solves this problem and the solution is known as the
Huber distribution (see [58]).
Huber's third problem is the robustification of the Neyman-Pearson test
theory. Given two distributions
denotes the Kolmogoroff metric. Under certain simplifying
assumptions Huber solves this problem and the solution is known as the
Huber distribution (see [58]).
Huber's third problem is the robustification of the Neyman-Pearson test
theory. Given two distributions ![]() and
and ![]() [76] derive the optimal test for testing
[76] derive the optimal test for testing ![]() against
against ![]() . Huber
considers full neighbourhoods
. Huber
considers full neighbourhoods
![]() of
of ![]() and
and
![]() of
of ![]() and then derives the form of the minimax test for the composite
hypothesis of
and then derives the form of the minimax test for the composite
hypothesis of
![]() against
against
![]() . The weakness of Huber's
approach is that it does not generalize easily to other
situations. Nevertheless it is the spirit of this approach which we
adopt here. It involves treating estimators as functionals on the
space of distributions, investigating where possible their behaviour over full
neighbourhoods and always being aware of the danger of a free lunch.
. The weakness of Huber's
approach is that it does not generalize easily to other
situations. Nevertheless it is the spirit of this approach which we
adopt here. It involves treating estimators as functionals on the
space of distributions, investigating where possible their behaviour over full
neighbourhoods and always being aware of the danger of a free lunch.
[51] introduced another approach to robustness, that based on
the influence function ![]() defined
for a statistical functional
defined
for a statistical functional ![]() as
follows
as
follows
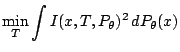 under (9.4) and under (9.4) and |
(9.5) |
Another approach which lies so to speak between that of Huber and
Hampel is the so called shrinking neighbourhood approach. It has
been worked out in full generality by [83]. Instead of
considering neighbourhoods of a fixed size (Huber) or only
infinitesimal neighbourhoods (Hampel) this approach considers full
neighbourhoods of a model but whose size decreases at the rate of
![]() as the sample size
as the sample size ![]() tends to infinity. The size of the
neighbourhoods is governed by the fact that for larger neighbourhoods
the bias term is dominant whereas models in smaller neighbourhoods
cannot be distinguished. The shrinking neighbourhoods approach has the
advantage that it does not need any assumptions of symmetry. The
disadvantage is that the size of the neighbourhoods goes to zero so
that the resulting theory is only robustness over vanishingly small
neighbourhoods.
tends to infinity. The size of the
neighbourhoods is governed by the fact that for larger neighbourhoods
the bias term is dominant whereas models in smaller neighbourhoods
cannot be distinguished. The shrinking neighbourhoods approach has the
advantage that it does not need any assumptions of symmetry. The
disadvantage is that the size of the neighbourhoods goes to zero so
that the resulting theory is only robustness over vanishingly small
neighbourhoods.
Although a statistic based on a data sample may be regarded as
a function of the data a more general approach is often useful. Given
a data set
![]() we define the corresponding empirical
distribution
we define the corresponding empirical
distribution ![]() by
by
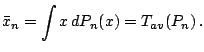 |
The space
![]() may be metricized in many ways but we prefer the
Kolmogoroff metric
may be metricized in many ways but we prefer the
Kolmogoroff metric ![]() defined
by
defined
by