Subsections

• 9.2.1 Location, Scale and Equivariance
• 9.2.2 Existence and Uniqueness
• 9.2.3 M-estimators
• 9.2.4 Bias and Breakdown
• 9.2.5 Confidence Intervals and Differentiability
• 9.2.6 Efficiency and Bias
• 9.2.7 Outliers in $\mathbb{R}$

9.2 Location and Scale in $\mathbb{R}$

9.2.1 Location, Scale and Equivariance

Changes in measurement units and baseline correspond to affine transformations on $\mathbb{R}$. We write

$$\mathcal{A}= \{A: \mathbb{R} \rightarrow \mathbb{R} \quad A(x)=ax+b,\, a\ne 0,\, b\in \mathbb{R}\}\,.$$ (9.14)

For any probability measure $P$ and for any $A \in\mathcal{A}$ we define

$$P^A(B)=P(\{x: A(x) \in B\}), \quad B \in \mathcal{B}\,,$$ (9.15)

$\mathcal{B}$ denoting all Borel sets on $\mathbb{R}$. Consider a subset $\mathcal{P}^{\prime}$ of $\mathcal{P}$ which is closed under affine transformations, that is

$$P \in \mathcal{P}^{\prime}\, \Rightarrow P^A \in \mathcal{P}^{\prime} P \in \mathcal{P}^{\prime},\, A \in \mathcal{A}\,.$$ (9.16)

A functional $T_l: \mathcal{P}^{\prime} \rightarrow \mathbb{R}$ will be called a location functional on $\mathcal{P}^{\prime}$ if

$$T_l(P^A)= A(T_l(P)),\quad A \in\mathcal{A},\, P \in \mathcal{P}^{\prime}\,.$$ (9.17)

Similarly we define a functional $T_s: \mathcal{P}^{\prime} \rightarrow \mathbb{R}_{+}$ to be a scale functional if

$$T_s(P^A)= \vert a \vert T_s(P),\quad A \in \mathcal{A},\, A(x)=ax+b,\, P \in \mathcal{P}^{\prime}\,.$$ (9.18)

9.2.2 Existence and Uniqueness

The fact that the mean $T_{av}$ of (9.7) cannot be defined for all distributions is an indication of its lack of robustness. More precisely the functional $T_{av}$ is not locally bounded (9.11) in the metric $d_{ko}$ at any distribution $P$. The median MED$(P)$ can be defined at any distribution $P$ as the mid-point of the interval of $m$-values for which

$$P((-\infty,m]) \ge 1/2 \quad P([m,\infty)) \ge 1/2\,.$$ (9.19)

Similar considerations apply to scale functionals. The standard deviation requires the existence of the second moment of a distribution. The median absolute deviation MAD (see [2]) of a distribution can be well defined at all distributions as follows. Given $P$ we define $P^{\prime}$ by

$$\notag P^{\prime}(B)=P(\{x: \vert x-\mathrm{MED}(P)\vert \in B\}), \quad B \in \mathcal{B}\,.$$

and set

$$\mathrm{MAD}(P) = \mathrm{MED}(P^{\prime})\,.$$ (9.20)

9.2.3 M-estimators

An important family of statistical functionals is the family of M-functionals introduced by [56] Let $\psi$ and $\chi$ be functions defined on $\mathbb{R}$ with values in the interval $[-1,\,1]$. For a given probability distribution $P$ we consider the following two equations for $m$ and $s$

$$\int \psi\left(\frac{x-m}{s}\right)\, {d}P(x)=\,$$ 0 (9.21)

$$\int \chi\left(\frac{x-m}{s}\right)\, {d}P(x)=\, 0 .$$ (9.22)

If the solution exists and is uniquely defined we denote it by

$$\notag T(P)=(T_l(P),T_s(P))=(m,s)\,.$$

In order to guarantee existence and uniqueness conditions have to be placed on the functions $\psi$ and $\chi$ as well as on the probability measure $P$. The ones we use are due to [99] (see also [58]) and are as follows:

( $\boldsymbol{\psi 1}$)	$\psi(-x)=-\psi(x)$ for all $x \in \mathbb{R}$.
( $\boldsymbol{\psi 2}$)	$\psi$ is strictly increasing
( $\boldsymbol{\psi 3}$)	$\lim_{x \rightarrow \infty} \psi(x) =1$
( $\boldsymbol{\psi 4}$)	$\psi$ is continuously differentiable with derivative $\psi^{(1)}$.
( $\boldsymbol{\chi 1}$)	$\chi(-x)=\chi(x)$ for all $x \in \mathbb{R}$.
( $\boldsymbol{\chi 2}$)	$\chi:\mathbb{R}_{+} \rightarrow [-1,\,1]$ is strictly increasing
( $\boldsymbol{\chi 3}$)	$\chi(0)=-1$
( $\boldsymbol{\chi 4}$)	$\lim_{x \rightarrow \infty} \chi(x) =1$
( $\boldsymbol{\chi 5}$)	$\chi$ is continuously differentiable with derivative $\chi^{(1)}$.
( $\boldsymbol{\psi \chi 1}$)	$\chi^{(1)}/\psi^{(1)}:\mathbb{R}_{+} \rightarrow \mathbb{R}_{+}$ is strictly increasing.

If these conditions hold and $P$ satisfies

$$\rm\Delta (P) = \max_x P(\{x\}) < 1/2$$ (9.23)

then (9.21) and (9.22) have precisely one solution. If we set

$$\notag \mathcal{P}^{\prime}=\{P: \rm\Delta (P) < 1/2\}$$

then $\mathcal{P}^{\prime}$ satisfies (9.16) and $T_l: \mathcal{P}^{\prime} \rightarrow \mathbb{R}$ and $T_s: \mathcal{P}^{\prime} \rightarrow \mathbb{R}_{+}$ are a location and a scale functional respectively. Two functions which satisfy the above conditions are

$$\psi(x) =\frac{\exp(x/c)-1}{\exp(x/c)+1}$$ (9.24)

$$\chi(x) =\frac{x^4-1}{x^4+1}\,,$$ (9.25)

where $c< 0.39$ is a tuning parameter. The restriction on $c$ is to guarantee $(\boldsymbol{\psi \chi 1})$. Algorithms for calculating the solution of (9.21) and (9.22) are given in the Fortran library ROBETH ([67]) which also contains many other algorithms related to robust statistics.

The main disadvantage of M-functionals defined by (9.21) and (9.22) is ( $\boldsymbol{\psi \chi 1}$) which links the location and scale parts in a manner which may not be desirable. In particular there is a conflict between the breakdown behaviour and the efficiency of the M-functional (see below). There are several ways of overcoming this. One is to take the scale function $T_s$ and then to calculate a second location functional by solving

$$\int {\tilde \psi}\left(\frac{x-m}{T_{s}(P)}\right)\,{d}P(x)=0\,.$$ (9.26)

If now ${\tilde \psi}$ satisfies ( $\boldsymbol{\psi 1}$)-( $\boldsymbol{\psi 4}$) then this new functional will exist only under the assumption that the scale functional exists and is non-zero. Furthermore the functional can be made as efficient as desired by a suitable choice of ${\tilde \psi}$ removing the conflict between breakdown and efficiency. One possible choice for $T_{s}(P)$ is the MAD of (9.20) which is simple, highly robust and which performed well in the Princeton robustness study ([2]).

In some situations there is an interest in downweighting outlying observations completely rather than in just bounding their effect. A downweighting to zero is not possible for a $\psi$-function which satisfies ( $\boldsymbol{\psi 2}$) but can be achieved by using so called redescending $\psi$-functions such as Tukey's biweight

$${ \tilde \psi}(x)=x(1-x^2)^2\{\vert x \vert \le 1\}\,.$$ (9.27)

In general there will be many solutions of (9.26) for such $\psi$-functions and to obtain a well defined functional some choice must be made. One possibility is to take the solution closest to the median, another is to take

$$\mathrm{argmin}_m \int \rho\left(\frac{x-m}{T_{s}(P)}\right)\,{d}P(x)$$ (9.28)

where $\rho^{(1)}= {\tilde \psi}$. Both solutions pose algorithmic problems. The effect of downweighting outlying observations to zero can be attained by using a so called one-step functional $T_{om}$ defined by

$$T_{om}(P) = T_m(P)+T_s(P)\frac{\int {\tilde \psi}\left(\frac{x-T_... ...}P(x)}{\int {\tilde \psi}^{(1)}\left(\frac{x-T_m(P)}{T_{s}(P)}\right)\,{d}P(x)}$$ (9.29)

where $T_m$ is as above and ${\tilde \psi}$ is redescending. We refer to [54] and [92] for more details.

So far all scale functionals have been defined in terms of a deviation from a location functional. This link can be broken as follows. Consider the functional $T_{ss}$ defined to be the solution $s$ of

$$\int \chi\left(\frac{x-y}{s}\right)\,{d}P(x)\,{d}P(y)=0\,\,,$$ (9.30)

where $\chi$ satisfies the conditions above. It may be shown that the solution is unique with $0 < s < \infty,$ if

$$\sum_{a_i} P(\{a_i\})^2 < 1/4\,\,,$$ (9.31)

where the $a_i$ denote the countably many atoms of $P$. The main disadvantage of this method is the computational complexity of (9.30) requiring as it does $\mathrm{O}(n^2)$ operations for a sample of size $n$. If $\chi$ is of the form

$$\notag \chi(x)=\left\{\begin{array}{ll} a >0,& \vert x\vert >1\\ b<0,& \vert x\vert \le 1\\ \end{array} \right.\,,$$

then $T_{ss}$ reduces to a quantile of the $\vert x_i-x_j\vert$ and much more efficient algorithms exist which allow the functional to be calculated in $\mathrm{O}(n\log n)$ operations (see [22], Rousseeuw and Croux (1992, 1993)).

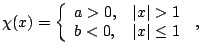Although we have defined $M$-functionals as a solution of (9.21) and (9.22) there are sometimes advantages in defining them as a solution of a minimization problem. Consider the Cauchy distribution with density

$$f(x:\mu,\sigma)= \frac{1}{\pi}\frac{\sigma}{\sigma^2+(x-\mu)^2}\,.$$ (9.32)

We now define ${\boldsymbol T}_{c}(P)=(T_{cm}(P),T_{cs}(P))$ by

$${\boldsymbol T}_{c}(P)= \mathrm{argmin}_{(m,s)}\left(-\int\log(\,f(x:m,s))\,{d}P(x)+ \frac{1}{2}\log(s)\right)\,.$$ (9.33)

This is simply the standard maximum likelihood estimate for a Cauchy distribution but there is no suggestion here that the data are so distributed. If $\rm\Delta (P) < 1/2$ it can be shown that the solution exists and is unique. Moreover there exists a simple convergent algorithm for calculating $(T_{cm}(P),T_{cs}(P))$ for a data sample. We refer to [61] for this and the multidimensional case to be studied below. By differentiating the right hand side of (9.33) it is seen that $(T_{cm}(P),T_{cs}(P))$ may be viewed as an M-functional with a redescending $\psi$-function.

Another class of functionals defined by a minimization problem is the class of $S$-functionals. Given a function $\rho: \mathbb{R} \rightarrow [0,\,1]$ which is symmetric, continuous on the right and non-increasing on $\mathbb{R}_{+}$ with $\rho(1)=1$ and $\lim_{x \rightarrow \infty}\rho(x)=0$. We define $(T_{sm}(P),T_{ss}(P))$ by

$$(T_{sm}(P),T_{ss}(P))=\mathrm{argmin}_{(m,s)} \left\{ s: \int\rho((x-m)/s)\,{d}P(x) \ge 1/2 \right\}\,.$$ (9.34)

A special case is a minor variation of the shortest-half functional of (9.8) which is obtained by taking $\rho$ to be the indicator function of the interval $[0,1)$. Although the existence of solutions of (9.34) is guaranteed if $\rm\Delta (P) < 1/2$ the problem of uniqueness is not trivial and requires the existence of a density subject to certain conditions. If $\rho$ is smooth then by differentiation it is seen that $(T_{sm}(P),T_{ss}(P))$ may be regarded as an M-functional with a redescending $\psi$-function given by ${\tilde \psi}=\rho^{(1)}$. The minimization problem (9.34) acts as a choice function. We refer to [23].

9.2.4 Bias and Breakdown

Given a location functional $T_l$ the bias is defined by

$$b(T_l,P,\epsilon,d_{ko}) = \sup \{\vert T_l(Q)-T_l(P)\vert: d_{ko}(P,Q) < \epsilon\}\,,$$ (9.35)

where by convention $T_l(Q) = \infty$ if $T_l$ is not defined at $Q$. For a scale functional $T_s$ we set

$$b(T_s,P,\epsilon,d_{ko}) = \sup \{\vert \log(T_s(Q)/T_s(P))\vert: d_{ko}(P,Q) < \epsilon\}\,,$$ (9.36)

where again by convention $T_s(Q) = \infty$ if $T_s$ is not defined at $Q$. A popular although weaker form of bias function based on the so called gross error neighbourhood is given by

$$b(T_l,P,\epsilon,GE) = \sup \{\vert T_l(Q)-T_l(P)\vert: Q=(1-\epsilon)P+\epsilon H, H \in \mathcal{P}\}$$ (9.37)

with a corresponding definition for $b(T_s,P,\epsilon,GE)$. We have

$$b(T_l,P,\epsilon,GE) \le b(T_l,P,\epsilon,d_{ko})\,.$$ (9.38)

We refer to [58] for more details.

The breakdown point $\epsilon^{\ast}(T_l,P,d_{ko})$ of $T_l$ at $P$ with respect to $d_{ko}$ is defined by

$$\epsilon^{\ast}(T_l,P,d_{ko})= \sup \{\epsilon: b(T_l,P,\epsilon,d_{ko})< \infty\}\,$$ (9.39)

with the corresponding definitions for scale functionals and the gross error neighbourhood. Corresponding to (9.38) we have

$$\epsilon^{\ast}(T_l,P,d_{ko}) \le \epsilon^{\ast}(T_l,P,GE)\,.$$ (9.40)

If a functional $T_l$ has a positive breakdown point at a distribution $P$ then it exhibits a certain degree of stability in a neighbourhood of $P$ as may be seen as follows. Consider a sample $x_1, \ldots, x_n$ and add to it $k$ further observations $x_{n+1},\ldots, x_{n+k}$. If $P_n$ and $P_{n+k}$ denote the empirical measures based on $x_1, \ldots, x_n$ and $x_1,\ldots,x_{n+k}$ respectively then $d_{ko}(P_n,P_{n+k})\le k/(n+k)$. In particular if $k/(n+k) < \epsilon^{\ast}(T_l,P_n,d_{ko})$ then it follows that $T_l(P_{n+k})$ remains bounded whatever the added observations . This finite sample concept of breakdown was introduced by [33]. Another version replaces $k$ observations by other values instead of adding $k$ observations and is as follows. Let $x^k_1,\ldots,x^k_n$ denote a sample differing from $x_1, \ldots, x_n$ in at most $k$ readings. We denote the empirical distributions by $P^k_n$ and define

$$\epsilon^{\ast}(T_l,P_n,fsbp)=\max \big\{k/n: \big\vert T_l\left(P^k_n\right) \big\vert < \infty\big\}\,,$$ (9.41)

where $P^k_n$ ranges over all possible $x^k_1,\ldots,x^k_n$. This version of the finite sample breakdown point is called the replacement version as $k$ of the original observations can be replaced by arbitrary values. The two breakdown points are related (see Zuo, 2001). There are corresponding versions for scale functionals.

For location and scale functionals there exist upper bounds for the breakdown points. For location functionals $T_l$ we have

Theorem 1  

$$\epsilon^{\ast}(T_l,P,d_{ko}) \le 1/2,$$ (9.42)

$$\epsilon^{\ast}(T_l,P,GE) \le 1/2,$$ (9.43)

$$\epsilon^{\ast}(T_l,P_n,fsbp) \le \lfloor n/2\rfloor/n.$$ (9.44)

We refer to [58]. It may be shown that all breakdown points of the mean are zero whereas the median attains the highest possible breakdown point in each case.The corresponding result for scale functionals is more complicated. Whereas we know of no reasonable metric in (9.42) of Theorem 1 which leads to a different upper bound this is not the case for scale functionals. [58] shows that for the Kolmogoroff metric $d_{ko}$ the corresponding upper bound is $1/4$ but is $1/2$ for the gross error neighbourhood. If we replace the Kolmogoroff metric $d_{ko}$ by the standard Kuiper metric $d_{ku}$ defined by

$$d_{ku}(P,Q) = \sup \{\vert P(I)-Q(I)\vert : I \}$$ (9.45)

then we again obtain an upper bound of $1/2$. For scale functionals $T_s$ we have

Theorem 2  

$$\epsilon^{\ast}(T_s,P,d_{ku}) \le (1-\rm\Delta (P))/2,$$ (9.46)

$$\epsilon^{\ast}(T_s,P,GE) \le (1-\rm\Delta (P))/2,$$ (9.47)

$$\epsilon^{\ast}(T_s,P_n,fsbp) \le (1-\rm\Delta (P))/2.$$ (9.48)

Similarly all breakdown points of the standard deviation are zero but, in contrast to the median, the MAD does not attain the upper bounds of (9.44). We have

$$\notag \epsilon^{\ast}({\mathrm{MAD}},P_n,fsbp)= \max\{0,\,1/2-\rm\Delta (P_n)\}\,.$$

A simple modification of the MAD, namely

$$\mathrm{MMAD}(P)=\min\{\vert I \vert: {\tilde P}(I)\ge (1+\rm\Delta (I))/2\}\,,$$ (9.49)

where ${\tilde P}(B)=P(\{x: \vert x-\mathrm{MED}(P)\vert \in B\})$ and $\rm\Delta (I)=\max\{P(\{x\}), x \in I\}$ can be shown to obtain the highest possible finite sample breakdown point of (9.48).

The M-functional defined by (9.21) and (9.22) has a breakdown point $\epsilon^{\ast}$ which satisfies

$$\psi^{-1}\left(\frac{\epsilon^{\ast}}{1-\epsilon^{\ast}}\right)= \chi^{-1}\left(\frac{-\epsilon^{\ast}}{1-\epsilon^{\ast}}\right)$$ (9.50)

(see [58]). For the functions defined by (9.24) and (9.25) the breakdown point is a decreasing function of $c$. As $c$ tends to zero the breakdown point tends to $1/2$. Indeed, as $c$ tends to zero the location part of the functional tends to the median. For $c=0.2$ numerical calculations show that the breakdown point is 0.48. The calculation of breakdown points is not always simple. We refer to [58] and [41].

The breakdown point is a simple but often effective measure of the robustness of a statistical functional. It does not however take into account the size of the bias. This can be done by trying to quantify the minimum bias over some neighbourhood of the distribution $P$ and if possible to identify a functional which attains it. We formulate this for $P=N(0,1)$ and consider the Kolmogoroff ball of radius $\epsilon$. We have ([58])

Theorem 3   For every $\epsilon < 1/2$ we have

$$\notag b({\mathrm{MED}},P,\epsilon,d_{ko}) \le b(T_l,P,\epsilon,d_{ko})$$

for any translation functional $T_l$.

In other words the median minimizes the bias over any Kolmogoroff neighbourhood of the normal distribution. This theorem can be extended to other symmetric distributions and to other situations (Riedel, 1989a, 1989b). It is more difficult to obtain such a theorem for scale functionals because of the lack of a property equivalent to symmetry for location. Nevertheless some results in this direction have been obtained and indicate that the length of the shortest half $T_{sh}$ of (9.8) has very good bias properties ([74]).

9.2.5 Confidence Intervals and Differentiability

Given a sample $x_1,\ldots,\,x_n$ with empirical measure $P_n$ we can calculate a location functional $T_l(P_n)$ which in some sense describes the location of the sample. Such a point value is rarely sufficient and in general should be supplemented by a confidence interval, that is a range of values consistent with the data. If $T_l$ is differentiable (9.12) and the data are i.i.d. random variables with distribution $P$ then it follows from (9.3) (see Sect. 9.1.3) that an asymptotic $\alpha$-confidence interval for $T_l(P)$ is given by

$$\left[T_l(P_n(P))-z((1+\alpha)/2)\Sigma(P)/\sqrt{n}, T_l(P_n(P))+z((1+\alpha)/2)\Sigma(P)/\sqrt{n}\right]\,.$$ (9.51)

Here $z(\alpha)$ denotes the $\alpha$-quantile of the standard normal distribution and

$$\Sigma(P)^2= \int I(x,T_l,P)^2\,{d}P(x)\,.$$ (9.52)

At first glance this cannot lead to a confidence interval as $P$ is unknown. If however $\Sigma(P)$ is also Fréchet differentiable at $P$ then we can replace $\Sigma(P)$ by $\Sigma(P_n(P))$ with an error of order $\mathrm{O}_P(1/\sqrt{n})$. This leads to the asymptotic $\alpha$-confidence interval

$$\left[T_l(P_n(P))-z((1+\alpha)/2)\Sigma(P_n(P))/\sqrt{n}, T_l(P_n(P))+z((1+\alpha)/2)\Sigma(P_n(P))/\sqrt{n}\right]\,.$$ (9.53)

A second problem is that (9.53) depends on asymptotic normality and the accuracy of the interval in turn will depend on the rate of convergence to the normal distribution which in turn may depend on $P$. Both problems can be overcome if $T_l$ is locally uniformly Fréchet differentiable at $P$. If we consider the M-functionals of Sect. 9.2.3 then they are locally uniformly Fréchet differentiable if the $\psi$- and $\chi$-functions are sufficiently smooth (see [11], [9], [10], and [27]). The influence function $I(\cdot,T_l,P)$ is given by

$$I(x,T_l,P)= T_s(P)\frac{D(P)\tilde\psi\left(\frac{x-T_l(P)}{T_s(P)}\right)- B(P)\chi\left(\frac{x-T_l(P)}{T_s(P)}\right)}{A(P)D(P)-B(P)C(P)}\,,$$ (9.54)

where

$$A(P) =\int\tilde\psi^{(1)}\left(\frac{x-T_l(P)}{T_s(P)}\right)\,{d}P(x)$$ (9.55)

$$B(P) =\int\left(\frac{x-T_l(P)}{T_s(P)}\right)\tilde\psi^{(1)}\left(\frac{x-T_l(P)}{T_s(P)}\right)\,{d}P(x)$$ (9.56)

$$C(P) =\int\chi^{(1)}\left(\frac{x-T_l(P)}{T_s(P)}\right)\,{d}P(x)$$ (9.57)

$$D(P) =\int\left(\frac{x-T_l(P)}{T_s(P)}\right)\chi^{(1)}\left(\frac{x-T_l(P)}{T_s(P)}\right)\,{d}P(x).$$ (9.58)

Simulations suggest that the covering probabilities of the confidence interval (9.53) are good for sample sizes of $20$ or more as long as the distribution $P$ is almost symmetric. For the sample $x_1, \ldots, x_n$ this leads to the interval

$$\left[T_l(P_n)-z((1+\alpha)/2)\Sigma(P_n)/\sqrt{n}, T_l(P_n)+z((1+\alpha)/2)\Sigma(P_n)/\sqrt{n}\right]$$ (9.59)

with $\Sigma(P)$ given by (9.52) and $I(x,T_l,P)$ by (9.54). Similar intervals can be obtained for the variations on M-functionals discussed in Sect. 9.2.3.

9.2.6 Efficiency and Bias

The precision of the functional $T$ at the distribution $P$ can be quantified by the length $2z((1+\alpha)/2)\Sigma(P)/\sqrt{n}$ of the asymptotic confidence interval (9.51). As the only quantity which depends on $T$ is $\Sigma(P)$ we see that an increase in precision is equivalent to reducing the size of $\Sigma(P)$. The question which naturally arises is then that of determining how small $\Sigma(P)$ can be made. A statistical functional which attains this lower bound is asymptotically optimal and if we denote this lower bound by $\Sigma_{\mathrm{opt}}(P)$, the efficiency of the functional $T$ can be defined as $\Sigma_{\mathrm{opt}}(P)^2/\Sigma(P)^2$. The efficiency depends on $P$ and we must now decide which $P$ or indeed $P$s to choose. The arguments given in Sect. 9.1.2 suggest choosing a $P$ which maximizes $\Sigma_{\mathrm{opt}}(P)$ over a class of models. This holds for the normal distribution which maximizes $\Sigma_{\mathrm{opt}}(P)$ over the class of all distributions with a given variance. For this reason and for simplicity and familiarity we shall take the normal distribution as the reference distribution. If a reference distribution is required which also produces outliers then the slash distribution is to be preferred to the Cauchy distribution. We refer to [19] and the discussion given there.

If we consider the M-functionals defined by (9.24) and (9.25) the efficiency at the normal distribution is an increasing function of the tuning parameter $c$. As the breakdown point is a decreasing function of $c$ this would seem to indicate that there is a conflict between efficiency and breakdown point. This is the case for the M-functional defined by (9.24) and (9.25) and is due to the linking of the location and scale parts of the functional. If this is severed by, for example, recalculating a location functional as in (9.26) then there is no longer a conflict between efficiency and breakdown. As however the efficiency of the location functional increases the more it behaves like the mean with a corresponding increase in the bias function of (9.35) and (9.37). The conflict between efficiency and bias is a real one and gives rise to an optimality criterion, namely that of minimizing the bias subject to a lower bound on the efficiency. We refer to [73].

9.2.7 Outliers in $\mathbb{R}$

One of the main uses of robust functionals is the labelling of so called outliers (see [5], [55], [3], [40], [42], and Simonoff (1984, 1987)). In the data of Table 9.1 the laboratories 1 and 3 are clearly outliers which should be flagged. The discussion in Sect. 9.1.1 already indicates that the mean and standard deviation are not appropriate tools for the identification of outliers as they themselves are so strongly influenced by the very outliers they are intended to identify. We now demonstrate this more precisely. One simple rule is to classify all observations more than three standard deviations from the mean as outliers. A simple calculation shows that this rule will fail to identify $10\,{\%}$ arbitrarily large outliers with the same sign. More generally if all observations more than $\lambda$ standard deviations from the mean are classified as outliers then this rule will fail to identify a proportion of $1/(1+\lambda^2)$ outliers with the same sign. This is known as the masking effect ([79]) where the outliers mask their presence by distorting the mean and, more importantly, the standard deviation to such an extent as to render them useless for the detection of the outliers. One possibility is to choose a small value of $\lambda$ but clearly if $\lambda$ is too small then some non-outliers will be declared as outliers. In many cases the main body of the data can be well approximated by a normal distribution so we now investigate the choice of $\lambda$ for samples of i.i.d. normal random variables. One possibility is to choose $\lambda$ dependent on the sample size $n$ so that with probability say 0.95 no observation will be flagged as an outlier. This leads to a value of $\lambda$ of about $\sqrt{2\log(n)}$ ([29]) and the largest proportion of one-sided outliers which can be detected is approximately $1/(1+2\log(n))$ which tends to zero with $n$. It follows that there is no choice of $\lambda$ which can detect say $10\,{\%}$ outliers and at the same time not falsely flag non-outliers. In order to achieve this the mean and standard deviation must be replaced by functionals which are less effected by the outliers. In particular these functionals should be locally bounded (9.11). Considerations of asymptotic normality or efficiency are of little relevance here. Two obvious candidates are the median and MAD and if we use them instead of the mean and standard deviation we are led to the identification rule ([53]) of the form

$$\vert x_i -\mathrm{MED}({\boldsymbol x}_n)\vert \ge \lambda \mathrm{MAD}({\boldsymbol x}_n)\,.$$ (9.60)

[52] proposed setting $\lambda=5.2$ as a general all purpose value. The concept of an outlier cannot in practice be very precise but in order to compare different identification rules we require a precise definition and a precise measure of performance. To do this we shall restrict attention to the normal model as one which is often reasonable for the main body of data. In other situations such as waiting times the exponential distribution may be more appropriate. The following is based on [29]. To define an outlier we introduce the concept of an $\alpha$-outlier. For the normal distribution $N(\mu, \sigma^2)$ and $\alpha\in (0,1)$ we define the $\alpha$-outlier region by

$${\mathrm{out}} (\alpha, N(\mu, \sigma^2))\; =\; \{x \in \mathbb{R}\!:\, \vert x - \mu\vert > \sigma\, z_{1 - \alpha/2}\}\,,$$ (9.61)

which is just the union of the lower and the upper $\alpha/2$-tail regions. Here $z_{1-\alpha/2}$ denotes the $1-\alpha/2$-quantile of the standard normal distribution. For the exponential distribution ${\mathrm{Exp}}(\lambda)$ with parameter $\lambda$ we set

$${\mathrm{out}}(\alpha, {\mathrm{Exp}}(\lambda))\; =\; \{x \in \mathbb{R}\!:\, x > - \lambda\, \ln \alpha \}$$ (9.62)

which is the upper $\alpha$-tail region ([43]). The extension to other distributions $P$ is clear. Each point located in the outlier region is called an $\alpha$-outlier, otherwise it is called an $\alpha$-inlier. This definition of an outlier refers only to its position in relation to the statistical model for the good data. No assumptions are made concerning the distribution of these outliers or the mechanism by which they are generated.

We can now formulate the task of outlier identification for the normal distribution as follows: For a given sample $\boldsymbol x_n = (x_1, \ldots, x_n)$ which contains at least $[n /2] + 1$ i.i.d. observations distributed according to $N(\mu, \sigma^2)$, we have to find all those $x_i$ that are located in ${\mathrm{out}}(\alpha, N(\mu, \sigma^2))$. The level $\alpha$ can be chosen to be dependent on the sample size. If for some $\tilde{\alpha} \in (0, 1)$ we set

$$\alpha\; =\; \alpha_n\; =\; 1 - (1 - \tilde{\alpha})^{1/n}\,,$$ (9.63)

then the probability of finding at least one observation of a $N(\mu, \sigma^2)$-sample of size $n$ within ${\mathrm{out}}(\alpha_n, N(\mu, \sigma^2))$ is not larger than $\tilde{\alpha}$. Consider now the general Hampel identifier which classifies all observations $x_i$ in

$${\mathrm{OR}}^H(\mathbf{x}_n, \alpha_n)\; =\; \{x \in \mathbb{R}\... ...m{Med}}(\mathbf{x}_n)\vert\; >\; g_n(\alpha_n)\; {\mathrm{MAD}}(\mathbf{x}_n)\}$$ (9.64)

as outliers. The region ${\mathrm{OR}}^H(\mathbf{x}_n, \alpha_n)$ may be regarded as an empirical version of the outlier region ${\mathrm{out}}(\alpha_n, N(\mu, \sigma^2))$. The constant $g_n(\alpha_n)$ standardizes the behaviour of the procedure for i.i.d. normal samples which may be done in several ways. One is to determine the constant so that with probability at least $1-\tilde{\alpha}$ no observation $X_i$ is identified as an outlier, that is

$$P \bigl( X_i \notin {\mathrm{OR}}(\mathbf{X}_n, \alpha_n),\; i = 1,\ldots,n \bigr)\; \ge\; 1 -\tilde{\alpha}.$$ (9.65)

A second possibility is to require that

$$P \bigl( {\mathrm{OR}}(\mathbf{X}_n, \alpha_n) \subset {\mathrm{out}}(\alpha_n, P) \bigr)\; \ge\; 1 -\tilde{\alpha}.$$ (9.66)

If we use (9.65) and set $\tilde{\alpha}=0.05$ then for $n=20, 50$ and $100\,\mathrm{simulations}$ give $g_n(\alpha_n)=5.82,\ 5.53$ and 5.52 respectively. For $n>10$ the normalizing constants $g_n(\alpha_n)$ can also be approximated according to the equations given in Sect. 5 of [40].

To describe the worst case behaviour of an outlier identifier we can look at the largest nonidentifiable outlier, which it allows. From [29] we report some values of this quantity for the Hampel identifier (HAMP) and contrast them with the corresponding values of a sophisticated high breakdown point outwards testing identifier (ROS), based on the non-robust mean and standard deviation ([87]; [107]). Both identifiers are standardized by (9.65) with $\tilde{\alpha}=0.05$. Outliers are then observations with absolute values greater than $3.016 (n=20)$, $3.284 (n=50)$ and $3.474 (n=100)$. For $k = 2$ outliers and $n=20$ the average sizes of the largest non-detected outlier are 6.68 (HAMP) and 8.77 (ROS), for $k=5$ outliers and $n=50$ the corresponding values are 4.64 (HAMP) and 5.91 (ROS) and finally for $k=15$ outliers and $n=100$ the values are 5.07 (HAMP) and 9.29 (ROS).