In the previous section we have seen that by restricting ourselves to linear functions one can control the complexity of a learning machine. We have thus avoided the problem of dealing with too complex functions at the price of being able to solve only linearly separable problems. In the following we will show how to extend the linear SVM for constructing a very rich set of non-linear decision functions while at the same time controlling their complexity.
Central to the success of support vector machines was the re-discovery of the so called Reproducing Kernel Hilbert Spaces (RKHS) and Mercer's Theorem ([12]). There is a large body of literature dealing with kernel functions, their theory and applicability, see e.g. [34], [3], [1], [12] or [59] for an overview. We only recall the basic definitions and properties necessary for turning our linear, hyperplane based learning technique into a very powerful algorithm capable of finding non-linear decision functions with controllable complexity.
The basic idea of the so called kernel-methods is to first
preprocess the data by some non-linear mapping ![]() and then to
apply the same linear algorithm as before but in the image space
of
and then to
apply the same linear algorithm as before but in the image space
of ![]() . (cf. Fig. 15.6 for an illustration).
More formally we apply the mapping
. (cf. Fig. 15.6 for an illustration).
More formally we apply the mapping
![\includegraphics[width=\textwidth]{text/3-15/spaces.eps}](img6898.gif)
|
In certain applications we might have sufficient knowledge about our
problem such that we can design an appropriate ![]() by hand
(e.g. [79,11]). If this mapping is
not too complex to compute and the space
by hand
(e.g. [79,11]). If this mapping is
not too complex to compute and the space
![]() is not too
high-dimensional, we might just explicitly apply this mapping to our
data. Something similar is done for (single hidden layer)
neural networks ([10]), radial basis networks
(e.g [42]) or
Boosting algorithms ([24]), where the input data are mapped
to some representation given by the hidden layer, the RBF bumps or the
hypotheses space, respectively ([52]). The
difference with kernel-methods is that for a suitably chosen
is not too
high-dimensional, we might just explicitly apply this mapping to our
data. Something similar is done for (single hidden layer)
neural networks ([10]), radial basis networks
(e.g [42]) or
Boosting algorithms ([24]), where the input data are mapped
to some representation given by the hidden layer, the RBF bumps or the
hypotheses space, respectively ([52]). The
difference with kernel-methods is that for a suitably chosen ![]() we
get an algorithm that has powerful non-linearities but is still very
intuitive and retains most of the favorable properties of its linear
input space version.
we
get an algorithm that has powerful non-linearities but is still very
intuitive and retains most of the favorable properties of its linear
input space version.
The problem with explicitly using the mapping ![]() to contruct
a feature space is that the resulting space can be extremely
high-dimensional. As an example consider the case when the input space
to contruct
a feature space is that the resulting space can be extremely
high-dimensional. As an example consider the case when the input space
![]() consists of images of
consists of images of
![]() pixels, i.e.
pixels, i.e. ![]() dimensional vectors, and we choose
dimensional vectors, and we choose ![]() th order monomials as non-linear
features. The dimensionality of such space would be
th order monomials as non-linear
features. The dimensionality of such space would be
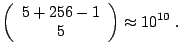 |
The problems concerning the storage and the manipulation of the high
dimensional data can be avoided. It turns out that for a certain class
of mappings we are well able to compute scalar products in this new
space even if it is extremely high dimensional. Simplifying the above
example of computing all ![]() th order products of
th order products of ![]() pixels to that
of computing all
pixels to that
of computing all ![]() nd order products of two ''pixels'', i.e.
nd order products of two ''pixels'', i.e.
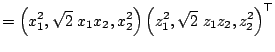 |
||
The kernel trick ([1,12,71]) is
to take the original algorithm and formulate it such, that we only use
![]() in scalar products. Then, if we can efficiently evaluate
these scalar products, we do not need to carry out the mapping
in scalar products. Then, if we can efficiently evaluate
these scalar products, we do not need to carry out the mapping ![]() explicitly and can still solve the problem in the huge feature
space
explicitly and can still solve the problem in the huge feature
space
![]() . Furthermore, we do not need to know the mapping
. Furthermore, we do not need to know the mapping ![]() but only the kernel function.
but only the kernel function.
Now we can ask two questions:
To address the question whether a kernel function
![]() is
a dot-product let us first introduce some more notation and
definitions. Given a training sample
is
a dot-product let us first introduce some more notation and
definitions. Given a training sample
![]() , the
, the ![]() matrix
matrix ![]() with
elements
with
elements
![]() is called the kernel matrix or the
Gram matrix. An
is called the kernel matrix or the
Gram matrix. An ![]() matrix
matrix ![]() (and any other symmetric
matrix) is said to be positive definite if any quadratic form over
(and any other symmetric
matrix) is said to be positive definite if any quadratic form over ![]() is positive, i.e. for all
is positive, i.e. for all
![]() ,
,
![]() , we have
, we have
For any positive definite kernel ![]() we can construct
a mapping
we can construct
a mapping ![]() into a feature space
into a feature space
![]() , such that
, such that ![]() acts as
a dot-product over
acts as
a dot-product over ![]() . As a matter of fact, it is possible to
construct more than one of these spaces. We will omit many crucial
details and only present the central results. For more details see
e.g. [59].
. As a matter of fact, it is possible to
construct more than one of these spaces. We will omit many crucial
details and only present the central results. For more details see
e.g. [59].
Given a real-valued, positive definite kernel function ![]() , defined
over a non-empty set
, defined
over a non-empty set
![]() , we define the feature space
, we define the feature space
![]() as the
space of all functions mapping from
as the
space of all functions mapping from
![]() to
to
![]() , i.e. as
, i.e. as
![]() . Notice that, unlike the example
in Fig. 15.6, this feature space is not a usual
Euclidean space but rather a vector space of functions. The mapping
. Notice that, unlike the example
in Fig. 15.6, this feature space is not a usual
Euclidean space but rather a vector space of functions. The mapping
![]() is now defined as
is now defined as
Let
![]() be a nonempty set and
be a nonempty set and
![]() a Hilbert space of functions
a Hilbert space of functions
![]() . Then
. Then
![]() is called
a reproducing kernel Hilbert space endowed with the dot
product
is called
a reproducing kernel Hilbert space endowed with the dot
product
![]() if there exists a function
if there exists a function
![]() with the properties that
with the properties that
One can show, that the kernel ![]() for such a RKHS is uniquely
determined.
for such a RKHS is uniquely
determined.
As a second way to identify a feature space associated with a kernel
![]() one can use a technique derived from Mercer's Theorem.
one can use a technique derived from Mercer's Theorem.
The Mercer's Theorem, which we will reproduce in the following, states
that if the function ![]() (the kernel) gives rise to a positive
integral operator, the evaluation of
(the kernel) gives rise to a positive
integral operator, the evaluation of
![]() can be expressed as
a finite or infinite, absolute and uniformly convergent series, almost
everywhere. This series then defines in another way
a feature space and an associated mapping connected to the kernel
can be expressed as
a finite or infinite, absolute and uniformly convergent series, almost
everywhere. This series then defines in another way
a feature space and an associated mapping connected to the kernel ![]() .
.
Let
![]() be a finite measure space, i.e. a space with
a
be a finite measure space, i.e. a space with
a ![]() -algebra and a measure
-algebra and a measure ![]() satisfying
satisfying
![]() .
.
Suppose
![]() is a symmetric real-valued function
such that the integral operator
is a symmetric real-valued function
such that the integral operator
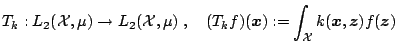 d d |
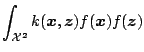 d d |
If we choose as feature space
![]() and the mapping
and the mapping
![]() as
as
The kernels satisfying the Mercer's Theorem are called Mercer
kernels. It can be shown that, if the set
![]() on which the kernel is
defined, is compact, a kernel is a Mercer kernel if and only if it is
a positive definite kernel (cf. [63]).
on which the kernel is
defined, is compact, a kernel is a Mercer kernel if and only if it is
a positive definite kernel (cf. [63]).
Table 15.1 lists some of the most widely used kernel functions. More sophisticated kernels (e.g. kernels generating splines or Fourier expansions) and kernels designed for special applications like DNA analysis can be found in [71], [65], [63], [28], [30], [79], [69] and numerous others.
Besides being useful tools for the computation of dot-products in
high- or infinite-dimensional spaces, kernels possess some additional
properties that make them an interesting choice in algorithms. It was
shown ([26]) that using a particular positive definite
kernel corresponds to an implicit choice of a regularization
operator. For translation-invariant kernels, the regularization
properties can be expressed conveniently in Fourier space in terms of
the frequencies ([63,25]). For example, Gaussian
kernels (cf. (15.16)) correspond to a general smoothness
assumption in all ![]() -th order derivatives ([63]). Vice
versa, using this correspondence, kernels matching a certain prior
about the frequency content of the data can be constructed so as to
reflect our prior problem knowledge.
-th order derivatives ([63]). Vice
versa, using this correspondence, kernels matching a certain prior
about the frequency content of the data can be constructed so as to
reflect our prior problem knowledge.
Another particularly useful feature of kernel functions is that we are
not restricted to kernels that operate on vectorial data,
e.g.
![]() . In principle, it is also possible to define positive
kernels for e.g. strings or graphs, i.e. making it possible to embed
discrete objects into a metric space and apply metric-based algorithms
(e.g. [28,76,79]).
. In principle, it is also possible to define positive
kernels for e.g. strings or graphs, i.e. making it possible to embed
discrete objects into a metric space and apply metric-based algorithms
(e.g. [28,76,79]).
Furthermore, many algorithms can be formulated using so called conditionally positive definite kernels (cf. [63,55]) which are a superclass of the positive definite kernels considered so far. They can be interpreted as generalized non-linear dissimilarity measures (opposed to just the scalar product) and are applicable e.g. in SVM and kernel PCA.