We are now at the point to merge the ideas of statistical learning,
Structural Risk Minimization and reproducing kernels into a single
algorithm, Support Vector Machines, suitable for a wide range of
practical application. The main goal of this algorithm is to find
a weight vector
![]() separating the data
separating the data
![]() with the largest
possible margin.
with the largest
possible margin.
Assume that the data are separable. Our goal is to find the smallest
possible
![]() without committing any error. This can be expressed by
the following quadratic optimization problem:
without committing any error. This can be expressed by
the following quadratic optimization problem:
In the formulation (15.20), refered to as the
primal formulation, we are bound to use the original data
![]() . In
order to apply the kernel trick (cf. Sect. 15.4.1) we
need to transform the problem such that the only operation involving
the original data
. In
order to apply the kernel trick (cf. Sect. 15.4.1) we
need to transform the problem such that the only operation involving
the original data
![]() is an inner product between certain data
points. This can be achieved by transforming the problem to the dual
formulation. The notion of duality is an essential part of non-linear
optimization theory, for details one can refer to any standard
textbook on mathematical programming (e.g. [38,9]). For
our purposes it is important that for every quadratic optimization
problem there exists a dual problem which is also a quadratic
problem. If both the primal and the dual problems have an optimal
solution then the values of the objective function at the optimal
solutions coincide. This implies that by solving the dual
problem - which uses the orginal data
is an inner product between certain data
points. This can be achieved by transforming the problem to the dual
formulation. The notion of duality is an essential part of non-linear
optimization theory, for details one can refer to any standard
textbook on mathematical programming (e.g. [38,9]). For
our purposes it is important that for every quadratic optimization
problem there exists a dual problem which is also a quadratic
problem. If both the primal and the dual problems have an optimal
solution then the values of the objective function at the optimal
solutions coincide. This implies that by solving the dual
problem - which uses the orginal data
![]() only through inner
products - the solution to the primal problem can be reconstructed.
only through inner
products - the solution to the primal problem can be reconstructed.
To derive the dual of (15.20), we introduce
Lagrange multipliers
![]() with
with
![]() , one for each of
the constraints in (15.20). We obtain the
following Lagrangian:
, one for each of
the constraints in (15.20). We obtain the
following Lagrangian:
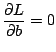 and and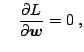 |
So far we have only considered the separable case which corresponds to an empirical error of zero (cf. Theorem 2). However for many practical applications this assumption is violated. If the data are not linearly separable then problem (15.20) has no feasible solution. By allowing for some errors we might get better results and avoid over-fitting effects (cf. Fig. 15.2).
Therefore a ''good'' trade-off between the empirical risk and the complexity term in (15.9) needs to be found. Using a technique which was first proposed in ([8]) and later used for SVMs in ([17]), one introduces slack-variables to relax the hard-margin constraints:
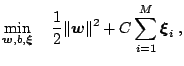 |
The threshold ![]() can be computed by exploiting the fact that for all
support vectors
can be computed by exploiting the fact that for all
support vectors
![]() with
with
![]() , the slack variable
, the slack variable
![]() is zero. This follows from the Karush-Kuhn-Tucker (KKT)
conditions (cf. (15.31) below). Thus, for any support vector
is zero. This follows from the Karush-Kuhn-Tucker (KKT)
conditions (cf. (15.31) below). Thus, for any support vector
![]() with
with
![]() holds:
holds:
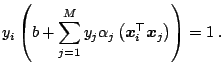 |
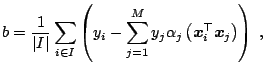 |
The Karush-Kuhn-Tucker (KKT) conditions are the necessary conditions for an optimal solution of a non-linear programming problem (e.g. [9,38]). The conditions are particularly simple for the dual SVM problem (15.28,15.29,15.30) ([70]):
The practical usefulness of SVM stems from their ability to provide
arbitrary non-linear separation boundaries and at the same time to
control generalization ability through the parameter ![]() and the
kernel parameters. In order to utilize these features it is necessary
to work with the dual formulation
(15.28)-(15.30) of
the SVM training problem. This can be difficult from the
computational point of view, for two reasons:
and the
kernel parameters. In order to utilize these features it is necessary
to work with the dual formulation
(15.28)-(15.30) of
the SVM training problem. This can be difficult from the
computational point of view, for two reasons:
The key idea of decomposition is to freeze all but a small number of optimization variables and to solve a sequence of constant-size problems. The set of variables optimized at a current iteration is referred to as the working set. Because the working set is re-optimized, the value of the objective function is improved at each iteration, provided the working set is not optimal before re-optimization.
The mathematics of the decomposition technique can be best seen in the
matrix notation. Let
![]() ,
let
,
let
![]() , let
, let ![]() be the matrix with the
entries
be the matrix with the
entries
![]() , and let
, and let
![]() denote
the vector of length
denote
the vector of length ![]() consisting of all
consisting of all ![]() s. Then the dual SVM
problem
(15.28)-(15.30) can
be written in the matrix form as:
s. Then the dual SVM
problem
(15.28)-(15.30) can
be written in the matrix form as:
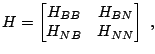 |
Iteration is carried out until the following termination criteria,
derived from Karush-Kuhn-Tucker conditions (15.31), are
satisfied to the required precision ![]() :
:
| (15.38) | ||||
| (15.39) | ||||
| (15.40) |
The crucial issue in the decomposition technique presented above is the selection of working sets. First, the provision that a working set must be sub-optimal before re-optimization is essential to prevent the algorithm from cycling. Second, the working set selection affects the speed of the algorithm: if sub-optimal working sets are selected more or less at random, the algorithm converges very slowly. Finally, the working set selection is important in theoretical analysis of decomposition algorithms; in particular in the convergence proofs and in the analysis of the convergence rate.
Two main approaches exist to the working set selection in the SVM
decomposition algorithms: the heuristic approach and the feasible
direction approach. The former has been used in the original paper of
[45] on SVM decomposition and has been mainly used in
the specific flavor of decomposition algorithms called Sequential
Minimal Optimization (SMO), presented in the next section. The
feasible direction decomposition algorithms root in the original
algorithm of [32] for pattern recognition
(
SVM![]() ), with the formal connection to the
feasible direction methods of nonlinear programming established by
[35].
), with the formal connection to the
feasible direction methods of nonlinear programming established by
[35].
The notion of a ''feasible direction'' stems from the classical
techniques of nonlinear programming subject to linear constraints
([80,9]). It refers to the direction along which any step
of the magnitude ![]() satisfying
satisfying
![]() , for
some fixed
, for
some fixed ![]() , results in a feasible solution to the nonlinear
program. For any nonlinear program, finding the feasible direction
amounts to a solution of a linear programming problem. In particular,
for the dual SVM training problem
(15.28)-(15.30) the
following problem must be solved:
, results in a feasible solution to the nonlinear
program. For any nonlinear program, finding the feasible direction
amounts to a solution of a linear programming problem. In particular,
for the dual SVM training problem
(15.28)-(15.30) the
following problem must be solved:
Convergence of the feasible direction SVM decomposition has been proved by [37], and the linear convergence rate has been observed experimentally ([35]).
The Sequential Minimal Optimization (SMO) algorithm proposed by [48] is another popular and efficient algorithm for the SVM training. In this algorithm the idea of decomposition is taken to its extreme by reducing the working sets to two points - the smallest size for which it is possible to maintain the equality constraint (15.30). With two points in the working set, the optimal solution can be computed analytically without calling an optimization tool.
The analytical computation of the optimal solution is based on the
following idea: given the solution
![]() , the optimal update is computed to obtain the
solution
, the optimal update is computed to obtain the
solution
![]() . To carry out
the update, first the constraints
(15.29)-(15.30)
have to be obeyed. The geometry of these constraints depends on
whether the labels
. To carry out
the update, first the constraints
(15.29)-(15.30)
have to be obeyed. The geometry of these constraints depends on
whether the labels ![]() and
and ![]() are equal or not. The two possible
configurations are shown in Fig. 15.7. If
are equal or not. The two possible
configurations are shown in Fig. 15.7. If
![]() (left picture) the solution should be sought along the line
(left picture) the solution should be sought along the line
![]() , where
, where
![]() If
If ![]() (right picture) the solution
should be sought along the line
(right picture) the solution
should be sought along the line
![]() . If the
solution transgresses the bound of the box, it should be clipped at
the bound.
. If the
solution transgresses the bound of the box, it should be clipped at
the bound.
The optimal values of the variables along the line are computed by
eliminating one of the variables through the equality constraint and
finding the unconstrained minimum of the objective function. Thus
eliminating ![]() one obtains the following update rule for
one obtains the following update rule for
![]() :
:
| (15.47) | |
| (15.48) | |
| (15.49) |
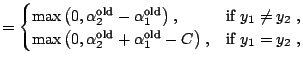 |
||
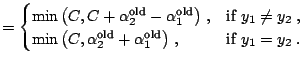 |
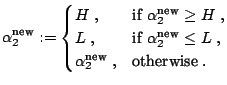 |
Many real-life machine learning problems can be more naturally viewed as online rather than batch learning problems. Indeed, the data are often collected continuously in time, and, more importantly, the concepts to be learned may also evolve in time. Significant effort has been spent in recent years on the development of the online SVM learning algorithms (e.g. [53,33,49]). An elegant solution to online SVM learning is the incremental SVM proposed by [16] which provides a framework for exact online learning.
To present the online SVM learning we first need an abstract formulation of the SVM optimization problem and a brief overview of the incremental SVM. We start with the following abstract form of the SVM optimization problem:
Incremental SVM provides a procedure for adding one example to an
existing optimal solution. When a new point ![]() is added, its weight
is added, its weight
![]() is initially assigned to 0. Then the weights of other
points and
is initially assigned to 0. Then the weights of other
points and ![]() should be updated, in order to obtain the optimal
solution for the enlarged dataset. Likewise, when a point
should be updated, in order to obtain the optimal
solution for the enlarged dataset. Likewise, when a point ![]() is to be
removed from the dataset, its weight is forced to 0, while updating
the weights of the remaining points and
is to be
removed from the dataset, its weight is forced to 0, while updating
the weights of the remaining points and ![]() so that the solution
obtained with
so that the solution
obtained with
![]() is optimal for the reduced dataset. The
online learning follows naturally from the incremental/decremental
learning: the new example is added while some old example is removed
from the working set.
is optimal for the reduced dataset. The
online learning follows naturally from the incremental/decremental
learning: the new example is added while some old example is removed
from the working set.
The basic principle of the incremental SVM ([16]) is that
updates to the state of the example ![]() should keep the
remaining examples in their optimal state. In other words, the KKT
conditions (15.31) expressed for the gradients
should keep the
remaining examples in their optimal state. In other words, the KKT
conditions (15.31) expressed for the gradients ![]() :
: