One extension of the SVM is that for the regression
task. In this subsection we will give a short overview of the idea of
Support Vector Regression (SVR).
A regression problem is given whenever
![]() for the training data
set
for the training data
set
![]() (cf. Sect. 15.2.1) and our interest is to find a function
of the form
(cf. Sect. 15.2.1) and our interest is to find a function
of the form
![]() (or more generally
(or more generally
![]() ).
).
In our discussion of the theoretical foundations of learning we have not yet talked about loss functions except for saying that they should be non-negative functions of the form (15.1). In the following we will discuss an interesting alternative for the problem of regression. There are two loss functions commonly used: the simple squared loss
In the left subplot of Fig. 15.8 the two error
functions are shown. In the right subplot a regression function using
the ![]() -insensitive loss function is shown for some artificial
data. The dashed lines indicate the boundaries of the area where the
loss is zero (the ''tube''). Clearly most of the data are within the
tube.
-insensitive loss function is shown for some artificial
data. The dashed lines indicate the boundaries of the area where the
loss is zero (the ''tube''). Clearly most of the data are within the
tube.
![\includegraphics[width=5cm]{text/3-15/regression_loss.eps}](img7075.gif)
![\includegraphics[width=5cm]{text/3-15/regression_tube.eps}](img7076.gif)
|
Similarly to the classification task, one is looking for the function
that best describes the values ![]() . In classification one is
interested in the function that separates two classes; in contrast, in
regression one looks for such a function that contains the given
dataset in its
. In classification one is
interested in the function that separates two classes; in contrast, in
regression one looks for such a function that contains the given
dataset in its ![]() -tube. Some data points can be allowed to lie
outside the
-tube. Some data points can be allowed to lie
outside the ![]() -tube by introducing the slack-variables.
-tube by introducing the slack-variables.
The primal formulation for the SVR is then given by:
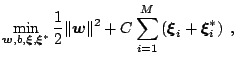 |
|
| subject to |
|
Another common problem of statistical learning is one-class classification (novelty detection). Its fundamental difference from the standard classification problem is that the training data is not identically distributed to the test data. The dataset contains two classes: one of them, the target class, is well sampled, while the other class it absent or sampled very sparsely. [56] have proposed an approach in which the target class is separated from the origin by a hyperplane. Alternatively ([67]), the target class can be modeled by fitting a hypersphere with minimal radius around it. We present this approach, schematically shown in Fig. 15.9, in more detail below.
![\includegraphics[width=4.5cm]{text/3-15/svdd.eps}](img7082.gif)
|
Mathematically the problem of fitting a hypersphere around the data is formalized as:
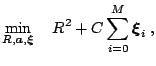 |
(15.57) |
| subject to |
|
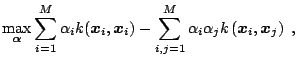 |
(15.58) |
| subject to |
|
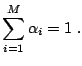 |
To decide whether a new object belongs to the target class one should determine its position with respect to the sphere using the formula