Subsections

• 16.2.1 Bagging
  • 16.2.1.1 Bagging algorithm
  
  
• 16.2.2 Unstable Estimators with Hard Decision Indicator
  • 16.2.2.1 Regression Trees
  
  
• 16.2.3 Subagging
  • 16.2.3.1 Subagging Algorithm
  • 16.2.3.2 Subagging Regression Trees
  
  
• 16.2.4 Bagging More ''Smooth'' Base Procedures and Bragging
• 16.2.5 Bragging
• 16.2.6 Out-of-Bag Error Estimation
• 16.2.7 Disadvantages
• 16.2.8 Other References

16.2 Bagging and Related Methods

Bagging ([9]), a sobriquet for bootstrap aggregating, is an ensemble method for improving unstable estimation or classification schemes. Breiman ([9]) motivated bagging as a variance reduction technique for a given base procedure, such as decision trees or methods that do variable selection and fitting in a linear model. It has attracted much attention, probably due to its implementational simplicity and the popularity of the bootstrap methodology. At the time of its invention, only heuristic arguments were presented why bagging would work. Later, it has been shown in ([18]) that bagging is a smoothing operation which turns out to be advantageous when aiming to improve the predictive performance of regression or classification trees. In case of decision trees, the theory in ([18]) confirms Breiman's intuition that bagging is a variance reduction technique, reducing also the mean squared error (MSE). The same also holds for subagging (subsample aggregating), defined in Sect. 16.2.3, which is a computationally cheaper version than bagging. However, for other (even ''complex'') base procedures, the variance and MSE reduction effect of bagging is not necessarily true; this has also been shown in ([20]) for the simple case where the estimator is a $U$-statistics.

16.2.1 Bagging

Consider the regression or classification setting. The data is given as in Sect. 16.1: we have pairs $(X_i,Y_i)\ (i=1,\ldots ,n)$, where $X_i \in \mathbb{R}^d$ denotes the $d$-dimensional predictor variable and the response $Y_i \in \mathbb{R}$ (regression) or $Y_i \in \{0,1,\ldots, J-1\}$ (classification with $J$ classes). The target function of interest is usually $\mathbb{E}[Y\vert X=x]$ for regression or the multivariate function $\mathbb{P}[Y=j\vert X=x]\ (j=0,\ldots ,J-1)$ for classification. The function estimator, which is the result from a given base procedure, is

$$\hat{g}(\cdot)=h_n ((X_1,Y_1),\ldots ,(X_n,Y_n))(\cdot):\ \mathbb{R}^d \to \mathbb{R}\;,$$

where the function $h_n(\cdot)$ defines the estimator as a function of the data.

Bagging is defined as follows.

16.2.1.1 Bagging algorithm

Step 1. Construct a bootstrap sample $(X_1^{\ast},Y_1^{\ast}),\ldots ,(X_n^{\ast},Y_n^{\ast})$ by randomly drawing $n$ times with replacement from the data $(X_1,Y_1),\ldots ,(X_n,Y_n)$.

Step 2. Compute the bootstrapped estimator $\hat{g}^{\ast}(\cdot)$ by the plug-in principle: $\hat{g}^{\ast}(\cdot) = h_n((X_1^{\ast},Y_1^{\ast}),\ldots ,(X_n^{\ast},Y_n^{\ast}))(\cdot)$.

Step 3. Repeat steps 1 and 2 $M$ times, where $M$ is often chosen as $50$ or $100$, yielding $\hat{g}^{\ast k}(\cdot)\ (k=1,\ldots ,M)$. The bagged estimator is $\hat{g}_{\text{Bag}}(\cdot) = M^{-1} \sum_{k=1}^M \hat{g}^{\ast k}(\cdot)$.

In theory, the bagged estimator is

$$\hat{g}_{\text{Bag}}(\cdot) = \mathbb{E}^{\ast}\left[\hat{g}^{\ast}(\cdot)\right]\;.$$ (16.2)

The theoretical quantity in (16.2) corresponds to $M = \infty$: the finite number $M$ in practice governs the accuracy of the Monte Carlo approximation but otherwise, it shouldn't be viewed as a tuning parameter for bagging. Whenever we discuss properties of bagging, we think about the theoretical version in (16.2).

This is exactly Breiman's ([9]) definition for bagging regression estimators. For classification, we propose to average the bootstrapped probabilities $\hat{g}_{j}^{\ast k}(\cdot) = {\hat{\mathbb{P}}}^{\ast}[Y^{\ast k}=j\vert X^{\ast k}=\cdot]\ (j=0,\ldots ,J-1)$ yielding an estimator for $\mathbb{P}[Y=j\vert X=\cdot]$ , whereas Breiman ([9]) proposed to vote among classifiers for constructing the bagged classifier.

The empirical fact that bagging improves the predictive performance of regression and classification trees is nowadays widely documented ([9], [10], [18], [26], [20,37]). To give an idea about the gain in performance, we cite some of the results of Breiman's pioneering paper ([9]): for $7$ classification problems, bagging a classification tree improved over a single classification tree (in terms of cross-validated misclassification error) by

$$33\,{\%} ,\; 47\,{\%} ,\; 30\,{\%} ,\; 23\,{\%} ,\; 20\,{\%} ,\; 22\,{\%} ,\; 27\,{\%} \;;$$

in case of $5$ regression data sets, bagging regression trees improved over a single regression tree (in terms of cross-validated squared error) by

$$39\,{\%} ,\; 22\,{\%} ,\; 46\,{\%} ,\; 30\,{\%} ,\; 38\,{\%} \;.$$

In both cases, the size of the single decision tree and of the bootstrapped trees was chosen by optimizing a $10$-fold cross-validated error, i.e. using the ''usual'' kind of tree procedure. Besides that the reported improvement in percentages is quite impressive, it is worth pointing out that bagging a decision tree is almost never worse (in terms of predictive power) than a single tree.

A trivial equality indicates the somewhat unusual approach of using the bootstrap methodology:

$$\hat{g}_{\text{Bag}}(\cdot) = \hat{g}(\cdot) + (\mathbb{E}^{\ast}... ...\ast}(\cdot)] - \hat{g}(\cdot)) = \hat{g}(\cdot) + \text{Bias}^{\ast}(\cdot)\;,$$

where Bias$^{\ast}(\cdot)$ is the bootstrap bias estimate of $\hat{g}(\cdot)$. Instead of the usual bias correction hwith a negative sign, bagging comes along with the wrong sign and adds the bootstrap bias estimate. Thus, we would expect that bagging has a higher bias than $\hat{g}(\cdot)$, which we will argue to be true in some sense, see Sect. 16.2.2. But according to the usual interplay between bias and variance in nonparametric statistics, the hope is to gain more by reducing the variance than increasing the bias, so that overall, bagging would pay-off in terms of the MSE. Again, this hope turns out to be true for some base procedures. In fact, Breiman ([9]) described heuristically the performance of bagging as follows: the variance of the bagged estimator $\hat{g}_{\text{Bag}}(\cdot)$ should be equal or smaller than that for the original estimator $\hat{g}(\cdot)$; and there can be a drastic variance reduction if the original estimator is ''unstable''.

16.2.2 Unstable Estimators with Hard Decision Indicator

Instability often occurs when hard decisions with indicator functions are involved as in regression or classification trees. One of the main underlying ideas why bagging works can be demonstrated by a simple example.

Example 1 (Toy Example: A Simple, Instructive Analysis)  

Consider the estimator

$$\hat{g}(x) = {\large {\text{\textbf{1}}}}_{[\overline{Y}_n \le x]}\;,\quad x \in \mathbb{R}\;,$$ (16.3)

where $\overline{Y}_n = n^{-1} \sum_{i=1}^n Y_i$ with $Y_1, \ldots, Y_n$ i.i.d. (no predictor variables $X_i$ are used for this example). The target we have in mind is $g(x) = \lim_{n \to \infty} \mathbb{E}[\hat{g}(x)]$. A simple yet precise analysis below shows that bagging is a smoothing operation. Due to the central limit theorem we have

$$n^{1/2} (\overline{Y}_n - \mu) \rightarrow_D \mathcal{N}(0, \sigma^2)\ (n \to \infty)$$ (16.4)

with $\mu = \mathbb{E}[Y_1]$ and $\sigma^2 = Var(Y_1)$. Then, for $x$ in a $n^{-1/2}$-neighborhood of $\mu$,

$$x=x_n(c) = \mu + c\sigma n^{-1/2}\;,$$ (16.5)

we have the distributional approximation

$$\hat{g}(x_n(c)) \rightarrow_D L(Z) = {\large {\text{\textbf{1}}}}_{[Z \le c]}\ (n \to \infty),\ Z \sim \mathcal{N}(0,1)\;.$$ (16.6)

Obviously, for a fixed $c$, this is a hard decision function of $Z$. On the other hand, averaging for the bagged estimator looks as follows. Denote by $\Phi(\cdot )$ the c.d.f. of a standard normal distribution:

$$\hat{g}_{\text{Bag}}(x_n(c)) = \mathbb{E}^{\ast}\left[{\large {\text{\textbf{1}}}}_{[\overline... ...)/\sigma \le n^{1/2} \left(x_n(c) - \overline{Y}_n\right)/\sigma\right]}\right]$$

$$= \Phi\left(n^{1/2}(x_n(c) - \overline{Y}_n)/\sigma\right) + o_P(1)$$

$$\rightarrow_D L_{\text{Bag}}(Z)=\Phi(c-Z)\quad (n \to \infty)\;,\quad Z \sim \mathcal{N}(0,1)\;,$$ (16.7)

where the first approximation (second line) follows because the bootstrap works for the arithmetic mean $\overline{Y}_n$, i.e.,

$$\sup_{x \in \mathbb{R}} \left\vert\mathbb{P}^{\ast}\left[n^{1/2} ... ...line{Y}_n)/\sigma \le x\right] - \Phi(x)\right\vert = o_P(1)\ (n \to \infty)\;,$$ (16.8)

and the second approximation (third line in (16.7) holds, because of (16.4) and the definition of $x_n(c)$ in (16.5). Comparing with (16.6), bagging produces a soft decision function $L_{\text{Bag}}(\cdot)$ of $Z$: it is a shifted inverse probit, similar to a sigmoid-type function. Figure 16.1 illustrates the two functions $L(\cdot)$ and $L_{\text{Bag}}(\cdot)$. We see that bagging is a smoothing operation. The amount of smoothing is determined ''automatically'' and turns out to be very reasonable (we are not claiming any optimality here). The effect of smoothing is that bagging reduces variance due to a soft-instead of a hard-thresholding operation.

We can compute the first two asymptotic moments in the unstable region with $x=x_n(c)$. Numerical evaluations of these first two moments and the mean squared error (MSE) are given in Fig. 16.2. We see that in the approximate range where $\vert c\vert \le 2.3$, bagging improves the asymptotic MSE. The biggest gain, by a factor $3$, is at the most unstable point $x=\mu = \mathbb{E}[Y_1]$, corresponding to $c=0$. The squared bias with bagging has only a negligible effect on the MSE (note the different scales in Fig. 16.2). Note that we always give an a-priori advantage to the original estimator which is asymptotically unbiased for the target as defined.

In ([18]), this kind of analysis has been given for more general estimators than $\overline{Y}_n$ in (16.3) and also for estimation in linear models after testing. Hard decision indicator functions are involved there as well and bagging reduces variance due to its smoothing effect. The key to derive this property is always the fact that the bootstrap is asymptotically consistent as in (16.8).

Figure 16.1: Indicator estimator from (16.3) at $x=x_n(0)$ as in (16.5). Function $L(z)= {\large{\text{\textbf{1}}}}_{[z \le 0]}$ (solid line) and $L_{\text {Bag}}(z)$ (dotted line) defining the asymptotics of the estimator in (16.6) and its bagged version in (16.7)

Figure 16.2: Indicator estimator from (16.3) at $x=x_n(c)$ as in (16.5). Asymptotic variance, squared bias and mean squared error (AMSE) (the target is $\lim_{n \to \infty} \mathbb{E}[\hat{g}(x)]$) for the estimator $\hat{g}(x_n(c))$ from (16.3) (solid line) and for the bagged estimator $\hat{g}_{\text{Bag}}(x_n(c))$ (dotted line) as a function of $c$

16.2.2.1 Regression Trees

We address here the effect of bagging in the case of decision trees which are most often used in practice in conjunction with bagging. Decision trees consist of piecewise constant fitted functions whose supports (for the piecewise constants) are given by indicator functions similar to (16.3). Hence we expect bagging to bring a significant variance reduction as in the toy example above.

For simplicity of exposition, we consider first a one-dimensional predictor space and a so-called regression stump which is a regression tree with one split and two terminal nodes. The stump estimator (or algorithm) is then defined as the decision tree,

$$\hat{g}(x) = \hat{\beta}_{\ell} {\large {\text{\textbf{1}}}}_{[x ... ...beta}_u - \hat{\beta}_{\ell}) {\large {\text{\textbf{1}}}}_{[\hat{d} \le x]}\;,$$ (16.9)

where the estimates are obtained by least squares as

$$(\hat{\beta}_\ell,\hat{\beta}_u,\hat{d}) = \mathop{\text{arg}}\ma... ...}}_{[X_i < d]} - \beta_u {\large {\text{\textbf{1}}}}_{[X_i \ge d]}\right)^2\;.$$

These values are estimates for the best projected parameters defined by

$$(\beta_{\ell}^0,\beta_u^0, d^0) = \mathop{\text{arg}}\mathop{\tex... ...1}}}}_{[X < d]} - \beta_u {\large {\text{\textbf{1}}}}_{[X \ge d]})^2\right]\;.$$ (16.10)

The main mathematical difference of the stump in (16.9) to the toy estimator in (16.3) is the behavior of $\hat{d}$ in comparison to the behavior of $\overline{Y}_n$ (and not the constants $\hat{\beta}_{\ell}$ and $\hat{\beta}_{u}$ involved in the stump). It is shown in ([18]) that $\hat{d}$ has convergence rate $n^{-1/3}$ (in case of a smooth regression function) and a limiting distribution which is non-Gaussian. This also explains that the bootstrap is not consistent, but consistency as in (16.8) turned out to be crucial in our analysis above. Bagging is still doing some kind of smoothing, but it is not known how this behaves quantitatively. However, a computationally attractive version of bagging, which has been found to perform often as good as bagging, turns out to be more tractable from a theoretical point of view.

16.2.3 Subagging

Subagging is a sobriquet for subsample aggregating where subsampling is used instead of the bootstrap for the aggregation. An estimator $\hat{g}(\cdot) = h_n((X_1,Y_1),\ldots ,(X_n,Y_n))(\cdot)$ is aggregated as follows:

$$\hat{g}_{SB(m)}(\cdot)= \left( \begin{array}{c} n\\ m \end{array}... ...) \in\, \mathcal{I}} h_m((X_{i_1},Y_{i_1}),\ldots ,(X_{i_m},Y_{i_m}))(\cdot)\;,$$

where $\mathcal{I}$ is the set of $m$-tuples ($m < n$) whose elements in $\{1,\ldots,n\}$ are all distinct. This aggregation can be approximated by a stochastic computation. The subagging algorithm is as follows.

16.2.3.1 Subagging Algorithm

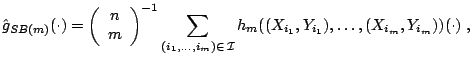Step 1. For $k=1,\ldots,M$ (e.g. $M = 50$ or $100$) do:

(i)  

Generate a random subsample $(X_1^{\ast k},Y_1^{\ast k}),\ldots ,(X_m^{\ast k},Y_m^{\ast k})$ by randomly drawing $m$ times without replacement from the data $(X_1,Y_1),\ldots ,(X_n,Y_n)$ (instead of resampling with replacement in bagging).

(ii)  

Compute the subsampled estimator

$$\hat{g}_{(m)}^{\ast k}(\cdot) = h_m\left((X_1^{\ast k},Y_1^{\ast k}),\ldots ,(X_m^{\ast k},Y_m^{\ast k})\right)(\cdot)\;;.$$

Step 2. Average the subsampled estimators to approximate

$$\hat{g}_{SB(m)}(\cdot ) \approx M^{-1} \sum_{k=1}^M \hat{g}_{(m)}^{\ast k}(\cdot)\;.$$

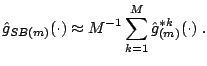As indicated in the notation, subagging depends on the subsample size $m$ which is a tuning parameter (in contrast to $M$).

An interesting case is half subagging with $m=[n/2]$. More generally, we could also use $m = [an]$ with $0<a<1$ (i.e. $m$ a fraction of $n$) and we will argue why the usual choice $m = o(n)$ in subsampling for distribution estimation ([44]) is a bad choice. Half subagging with $m=[n/2]$ has been studied also in ([20]): in case where $\hat{g}$ is a $U$-statistic, half subagging is exactly equivalent to bagging, and subagging yields very similar empirical results to bagging when the estimator $\hat{g}(\cdot)$ is a decision tree. Thus, if we don't want to optimize over the tuning parameter $m$, a good choice in practice is very often $m=[n/2]$. Consequently, half subagging typically saves more than half of the computing time because the computational order of an estimator $\hat{g} = \hat{g}_{(n)}$ is usually at least linear in $n$.

16.2.3.2 Subagging Regression Trees

We describe here in a non-technical way the main mathematical result from ([18]) about subagging regression trees.

The underlying assumptions for some mathematical theory are as follows. The data generating regression model is

$$Y_i = g(X_i) + \varepsilon_i\;,\quad i=1,\ldots ,n\;,$$

where $X_1, \ldots, X_n$ and $\varepsilon_1,\ldots ,\varepsilon_n$ are i.i.d. variables, independent from each other, and $\mathbb{E}[\varepsilon_1]=0$, $\mathbb{E}\vert\varepsilon_1\vert^2 < \infty$. The regression function $g(\cdot)$ is assumed to be smooth and the distribution of $X_i$ and $\varepsilon_i$ are assumed to have suitably regular densities.

It is then shown in ([18]) that for $m = [an]\ (0<a<1)$,

$$\limsup_{n \to \infty} \frac{\mathbb{E}\left[(\hat{g}_{SB(m)}(x) - g(x))^2\right]}{\mathbb{E}\left[(\hat{g}_{n}(x) - g(x))^2\right]} < 1\;,$$

for $x$ in suitable neighborhoods (depending on the fraction $a$) around the best projected split points of a regression tree (e.g. the parameter $d^0$ in (16.10) for a stump), and where $g(x) = \lim_{n \to \infty} \mathbb{E}[\hat{g}(x)]$. That is, subagging asymptotically reduces the MSE for $x$ in neighborhoods around the unstable split points, a fact which we may also compare with Fig. 16.2. Moreover, one can argue that globally,

$$\mathbb{E}\left[(\hat{g}_{SB(m)}(X) - g(X))^2\right] \buildrel{{\text{approx.}}} \over < \mathbb{E}\left[(\hat{g}(X) - g(X))^2\right]$$

for $n$ large, and where the expectations are taken also over (new) predictors $X$.

For subagging with small order $m = o(n)$, such a result is no longer true: the reason is that small order subagging will then be dominated by a large bias (while variance reduction is even better than for fraction subagging with $m = [an],\ 0<a<1$).

Similarly as for the toy example in Sect. 16.2.2, subagging smoothes the hard decisions in a regression tree resulting in reduced variance and MSE.

16.2.4 Bagging More ''Smooth'' Base Procedures and Bragging

As discussed in Sects. 16.2.2 and 16.2.3, (su-)bagging smoothes out indicator functions which are inherent in some base procedures such as decision trees. For base procedures which are ''smoother'', e.g. which do not involve hard decision indicators, the smoothing effect of bagging is expected to cause only small effects.

For example, in ([20]) it is proved that the effect of bagging on the MSE is only in the second order term if the base procedure is a $U$-statistic. Similarly, citing ([23]): ''$\ldots$ when bagging is applied to relatively conventional statistical problems, it cannot reliably be expected to improve performance''. On the other hand, we routinely use nowadays ''non-conventional'' methods: a simple example is variable selection and fitting in a linear model where bagging has been demonstrated to improve predictive performance ([9]).

In ([26]), the performance of bagging has been studied for MARS, projection pursuit regression and regression tree base procedures: most improvements of bagging are reported for decision trees. In ([18]), it is shown that bagging the basis function in MARS essentially doesn't change the asymptotic MSE. In ([15]) it is empirically demonstrated in greater detail that for finite samples, bagging MARS is by far less effective - and sometimes very destructive - than bagging decision trees.

(Su-)bagging may also have a positive effect due to averaging over different selected predictor variables; this is an additional effect besides smoothing out indicator functions. In case of MARS, we could also envision that such an averaging over different selected predictor variables would have a positive effect: in the empirical analysis in ([15]), this has been found to be only true when using a robust version of aggregation, see below.

16.2.5 Bragging

Bragging stands for bootstrap robust aggregating ([15]): it uses the sample median over the $M$ bootstrap estimates $\hat{g}^{\ast k}(\cdot)$, instead of the sample mean in Step 3 of the bagging algorithm.

While bragging regression trees was often found to be slightly less improving than bagging, bragging MARS seems better than the original MARS and much better than bagging MARS.

16.2.6 Out-of-Bag Error Estimation

Bagging ''automatically'' yields an estimate of the out-of-sample error, sometimes referred to as the generalization error. Consider a loss $\ell(Y,\hat{g}(X))$, measuring the discrepancy between an estimated function $\hat{g}$, evaluated at $X$, and the corresponding response $Y$, e.g. $\ell(Y,\hat{g}(X)) = \vert Y - \hat{g}(X)\vert^2$. The generalization error is then

$$err = \mathbb{E}\left[\ell(Y,\hat{g}(X))\right]\;,$$

where the expectation $\mathbb{E}$ is over the training data $(X_1,Y_1),\ldots ,(X_n,Y_n)$ (i.i.d. or stationary pairs), $\hat{g}(\cdot)$ a function of the training data, and $(X,Y)$ is a new test observation, independent from the training data but having the same distribution as one training sample point $(X_i, Y_i)$.

In a bootstrap sample (in the bagging procedure), roughly $exp(-1) \approx 37\,{\%}$ of the original observations are left out: they are called ''out-of-bag'' observations ([10]). Denote by $\mathcal{B}oot^k$ the original sample indices which were resampled in the $k$th bootstrap sample; note that the out-of-bag sample observations (in the $k$th bootstrap resampling stage) are then given by $\{1,\ldots ,n\} \setminus \mathcal{B}oot^k$ which can be used as test sets. The out-of-bag error estimate of bagging is then defined as

$$\widehat{err}_{OB} = n^{-1} \sum_{i=1}^n N_M^{-1} \sum_{k=1}^M {\... ...) \notin \mathcal{B}oot^k\right]} \ell\left(Y_i,\hat{g}^{\ast k}(X_i)\right)\;,$$

$$N_M = \sum_{k=1}^M {\large {\text{\textbf{1}}}}_{\left[(X_i,Y_i) \notin \mathcal{B}oot^k\right]}\;.$$

In ([21]), a correction of the out-of-bag error estimate is proposed. Out-of-bag estimation can also be used for other tasks, e.g. for more honest class probability estimates in classification when bagging trees ([10]).

16.2.7 Disadvantages

The main disadvantage of bagging, and other ensemble algorithms, is the lack of interpretation. A linear combination of decision trees is much harder to interpret than a single tree. Likewise: bagging a variable selection - fitting algorithm for linear models (e.g. selecting the variables using the AIC criterion within the least-squares estimation framework) gives little clues which of the predictor variables are actually important.

One way out of this lack of interpretation is sometimes given within the framework of bagging. In ([28]), the bootstrap has been justified to judge the importance of automatically selected variables by looking at relative appearance-frequencies in the bootstrap runs. The bagging estimator is the average of the fitted bootstrap functions, while the appearance frequencies of selected variables or interactions may serve for interpretation.

16.2.8 Other References

Bagging may also be useful as a ''module'' in other algorithms: BagBoosting ([17]) is a boosting algorithm (see Sect. 16.3) with a bagged base-procedure, often a bagged regression tree. The theory about bagging supports the finding that BagBoosting using bagged regression trees, which have smaller asymptotic MSEs than trees, is often better than boosting with regression trees. This is empirically demonstrated for a problem about tumor classification using microarray gene expression predictors ([24]).

Bundling classifiers ([37]), which is a more complicated aggregation algorithm but related to bagging, seems to perform better than bagging for classification. In ([45]), bagging is used in conjunction with boosting (namely for stopping boosting iterations) for density estimation. In ([27]), bagging is used in the unsupervised context of cluster analysis, reporting improvements when using bagged clusters instead of original cluster-outputs.