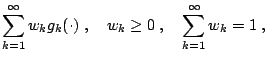



Next: References
Up: 16. Bagging, Boosting and
Previous: 16.2 Bagging and Related
Subsections
16.3 Boosting
Boosting algorithms have been prpoposed in the machine learning
literature by Schapire ([47]) and Freund
([30], [31]), see also ([48]). These first
algorithms have been developed as ensemble methods. Unlike bagging
which is a parallel ensemble method, boosting methods are
sequential ensemble algorithms where the weights 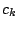 in
(16.1) are depending on the previous fitted functions
in
(16.1) are depending on the previous fitted functions
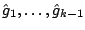 . Boosting has been empirically
demonstrated to be very accurate in terms of classification,
notably the so-called AdaBoost algorithm ([31]).
. Boosting has been empirically
demonstrated to be very accurate in terms of classification,
notably the so-called AdaBoost algorithm ([31]).
We will explain below that boosting can be viewed as
a nonparametric optimization algorithm in function space, as first
pointed out by Breiman ([11], [12]). This view turns
out to be very fruitful to adapt boosting for other problems than
classification, including regression and survival analysis.
Maybe it is worth mentioning here that boosting algorithms have often
better predictive power than bagging, (cf. ([11])); of course,
such a statement has to be read with caution, and methods should be
tried out on individual data-sets, including e.g. cross-validation,
before selecting one among a few methods.
To give an idea, we report here some empirical results
from ([11]) for classification: we show below the gains (in
percentage) of boosting trees over bagging trees:
| |
''normal'' size data-sets: |
|
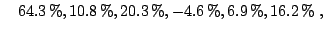 |
|
| |
large data-sets: |
|
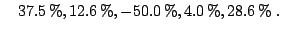 |
|
For all data-sets, boosting trees was better than a single
classification tree. The biggest loss of 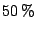 for boosting in
comparison with bagging is for a data-set with very low
misclassification error, where bagging achieves
for boosting in
comparison with bagging is for a data-set with very low
misclassification error, where bagging achieves
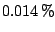 and
boosting
and
boosting
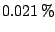 .
.
16.3.1 Boosting as Functional Gradient Descent
Rather than looking through the lenses of ensemble methods, boosting
algorithms can be seen as functional gradient descent techniques
([11], [12]). The goal is to estimate a function
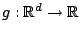 , minimizing an expected loss
, minimizing an expected loss
![$\displaystyle \mathbb{E}\left[\ell(Y,g(X))\right]\;,\ \ell(\cdot,\cdot): \mathbb{R} \times \mathbb{R} \to \mathbb{R}^{+}\;,$](img7212.gif) |
(16.11) |
based on data
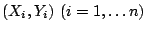 as in
Sect. 16.2.1. The loss function
as in
Sect. 16.2.1. The loss function 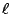 is typically assumed
to be convex in the second argument. We consider here both cases where
the univariate response
is typically assumed
to be convex in the second argument. We consider here both cases where
the univariate response 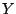 is continuous (regression problem) or
discrete (classification problem), since boosting is potentially
useful in both cases.
is continuous (regression problem) or
discrete (classification problem), since boosting is potentially
useful in both cases.
As we will see in Sect. 16.3.2, boosting algorithms are
pursuing a ''small'' empirical risk
by selecting a  in the linear hull of some function class,
i.e.
in the linear hull of some function class,
i.e.
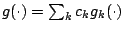 with
with
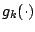 's from
a function class such as trees.
's from
a function class such as trees.
The most popular loss functions, for regression and binary
classification, are given in Table 16.1.
Table 16.1:
The squared error, binomial negative log-likelihood and exponential
loss functions and their population minimizers; logit 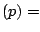 log
log 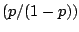
| Boosting |
Loss function |
Population minimizer for (16.11) |
 Boost Boost |
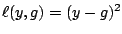 |
![$ g(x) = \mathbb{E}[Y\vert X=x]$](img7218.gif) |
| LogitBoost |
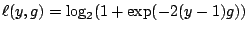 |
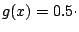 logit logit![$ (\mathbb{P}[Y=1\vert X=x])$](img7221.gif) |
| AdaBoost |
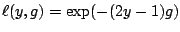 |
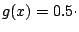 logit logit![$ (\mathbb{P}[Y=1\vert X=x])$](img7221.gif) |
While the squared error loss is mainly used for regression
(see ([19]) for classification with the squared error loss), the
log-likelihood and the exponential loss are for binary classification
only.
The form of the log-likelihood loss may be somewhat unusual: we norm
it, by using the base 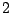 so that it ''touches'' the
misclassification error as an upper bound (see Fig. 16.3),
and we write it as a function of the so-called margin
so that it ''touches'' the
misclassification error as an upper bound (see Fig. 16.3),
and we write it as a function of the so-called margin
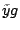 , where
, where
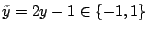 is the usual
labeling from the machine learning community. Thus, the loss is
a function of the margin
is the usual
labeling from the machine learning community. Thus, the loss is
a function of the margin
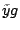 only; and the same is true with
the exponential loss and also the squared error loss for
classification since
only; and the same is true with
the exponential loss and also the squared error loss for
classification since
using
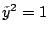 .
.
Figure 16.3:
Loss functions of the margin for binary
classification. Zero-one misclassification loss (solid line),
log-likelihood loss (dashed line), exponential loss (dotted
line), squared error loss (dashed/dotted). The loss-functions are described in
Table 16.1
|
|
The misclassification loss, or zero-one loss, is
![$ {\large {\text{\textbf{1}}}}_{[\tilde{y}g
<0]}$](img7228.gif) , again a function of the margin, whose population minimizer is
, again a function of the margin, whose population minimizer is
![$ g(x) = {\large {\text{\textbf{1}}}}_{\left[\mathbb{P}[Y=1\vert X=x] > 1/2\right]}$](img7229.gif) . For readers less
familiar with the concept of the margin, this can also be understood
as follows: the Bayes-classifier which minimizes the misclassification
risk is
. For readers less
familiar with the concept of the margin, this can also be understood
as follows: the Bayes-classifier which minimizes the misclassification
risk is
We can now see that a misclassification occurs, if
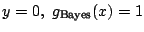 or
or 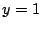 ,
,
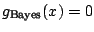 , which is
equivalent to
, which is
equivalent to
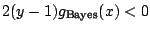 or
or
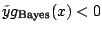 .
.
The (surrogate) loss functions given in Table 16.1 are all
convex functions of the margin
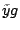 which bound the zero-one
misclassification loss from above, see Fig. 16.3. The
convexity of these surrogate loss functions is computationally
important for empirical risk minimization; minimizing the empirical
zero-one loss is computationally intractable.
which bound the zero-one
misclassification loss from above, see Fig. 16.3. The
convexity of these surrogate loss functions is computationally
important for empirical risk minimization; minimizing the empirical
zero-one loss is computationally intractable.
16.3.2 The Generic Boosting Algorithm
Estimation of the function 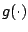 , which minimizes an expected
loss in (16.11), is pursued by a constrained
minimization of the empirical risk
, which minimizes an expected
loss in (16.11), is pursued by a constrained
minimization of the empirical risk
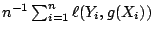 . The constraint comes in algorithmically (and
not explicitly), by the way we are attempting to minimize the
empirical risk, with a so-called functional gradient descent. This
gradient descent view has been recognized and refined by various
authors (cf. ([11], [12], [43], [34],
[33], [19])). In summary, the minimizer of the
empirical risk is imposed to satisfy a ''smoothness'' constraint
in terms of a linear expansion of (''simple'') fits from
a real-valued base procedure function estimate.
. The constraint comes in algorithmically (and
not explicitly), by the way we are attempting to minimize the
empirical risk, with a so-called functional gradient descent. This
gradient descent view has been recognized and refined by various
authors (cf. ([11], [12], [43], [34],
[33], [19])). In summary, the minimizer of the
empirical risk is imposed to satisfy a ''smoothness'' constraint
in terms of a linear expansion of (''simple'') fits from
a real-valued base procedure function estimate.
Step 1 (initialization). Given data
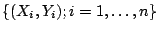 , apply the base procedure yielding the function estimate
, apply the base procedure yielding the function estimate
where
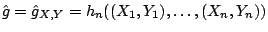 is
a function of the original data. Set
is
a function of the original data. Set 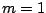 .
.
Step 2 (projecting gradient to learner). Compute the
negative gradient vector
evaluated at the current
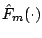 . Then, apply the base
procedure to the gradient vector
. Then, apply the base
procedure to the gradient vector
where
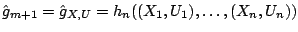 is a function of the original predictor variables and the
current negative gradient vector as pseudo-response.
is a function of the original predictor variables and the
current negative gradient vector as pseudo-response.
Step 3 (line search). Do a one-dimensional numerical search for the
best step-size
Update,
Step 4 (iteration). Increase 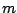 by one and repeat
Steps 2 and 3 until a stopping iteration
by one and repeat
Steps 2 and 3 until a stopping iteration 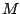 is achieved.
is achieved.
The number of iterations 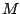 is the tuning parameter of boosting. The
larger it is, the more complex the estimator. But the complexity, for
example the variance of the estimator, is not linearly increasing in
is the tuning parameter of boosting. The
larger it is, the more complex the estimator. But the complexity, for
example the variance of the estimator, is not linearly increasing in
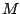 : instead, it increases very slowly as
: instead, it increases very slowly as 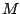 gets larger, see also
Fig. 16.4 in Sect. 16.3.5.
gets larger, see also
Fig. 16.4 in Sect. 16.3.5.
Obviously, the choice of the base procedure influences the boosting
estimate. Originally, boosting has been mainly used with tree-type
base procedures, typically with small trees such as stumps (two
terminal nodes) or trees having say 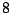 terminal nodes
(cf. ([11], [14], [7], [34],
[25])); see also
Sect. 16.3.8. But we will demonstrate in
Sect. 16.3.6 that boosting may be very worthwhile within
the class of linear, additive or interaction models, allowing for good
model interpretation.
terminal nodes
(cf. ([11], [14], [7], [34],
[25])); see also
Sect. 16.3.8. But we will demonstrate in
Sect. 16.3.6 that boosting may be very worthwhile within
the class of linear, additive or interaction models, allowing for good
model interpretation.
The function estimate
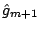 in Step 2 can be viewed as an
estimate of
in Step 2 can be viewed as an
estimate of
![$ \mathbb{E}[U_i\vert X=x]$](img7246.gif) , the expected negative gradient given the
predictor
, the expected negative gradient given the
predictor 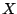 , and takes values in
, and takes values in
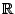 , even in case of
a classification problem with
, even in case of
a classification problem with 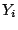 in a finite set (this is different
from the AdaBoost algorithm, see below).
in a finite set (this is different
from the AdaBoost algorithm, see below).
We call
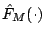 the
the  Boost-, LogitBoost- or
AdaBoost-estimate, according to the implementing loss function
Boost-, LogitBoost- or
AdaBoost-estimate, according to the implementing loss function
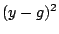 ,
,
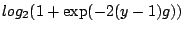 or
or
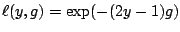 ,
respectively; see Table 16.1.
,
respectively; see Table 16.1.
The original AdaBoost algorithm for classification is actually a bit
different: the base procedure fit is a classifier, and not
a real-valued estimator for the conditional probability of 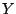 given
given
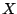 ; and Steps 2 and 3 are also somewhat different. Since AdaBoost's
implementing exponential loss function is not well established in
statistics, we refer for a detailed discussion to ([34]). From
a statistical perspective, the squared error loss and log-likelihood
loss functions are most prominent and we describe below the
corresponding boosting algorithms in detail.
; and Steps 2 and 3 are also somewhat different. Since AdaBoost's
implementing exponential loss function is not well established in
statistics, we refer for a detailed discussion to ([34]). From
a statistical perspective, the squared error loss and log-likelihood
loss functions are most prominent and we describe below the
corresponding boosting algorithms in detail.
Boosting using the squared error loss,  Boost, has a simple
structure: the negative gradient in Step 2 is the classical residual
vector and the line search in Step 3 is trivial when using a base
procedure which does least squares fitting.
Boost, has a simple
structure: the negative gradient in Step 2 is the classical residual
vector and the line search in Step 3 is trivial when using a base
procedure which does least squares fitting.
Step 1 (initialization). As in Step 1 of generic functional gradient
descent.
Step 2. Compute residuals
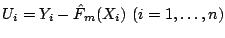 and fit the real-valued base procedure to the current residuals
(typically by (penalized) least squares) as in Step 2 of the generic
functional gradient descent; the fit is
denoted by
and fit the real-valued base procedure to the current residuals
(typically by (penalized) least squares) as in Step 2 of the generic
functional gradient descent; the fit is
denoted by
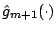 .
.
Update
We remark here that, assuming the base procedure does some
(potentially penalized) least squares fitting of the residuals, the
line search in Step 3 of the generic algorithm becomes trivial with
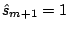 .
.
Step 3 (iteration). Increase iteration
index 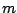 by one and repeat Step 2 until a stopping iteration
by one and repeat Step 2 until a stopping iteration 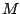 is
achieved.
is
achieved.
The estimate
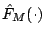 is an estimator of the
regression function
is an estimator of the
regression function
![$ \mathbb{E}[Y\vert X=\cdot]$](img7254.gif) .
.  Boosting is nothing else
than repeated least squares fitting of residuals
(cf. ([33], [19])). With
Boosting is nothing else
than repeated least squares fitting of residuals
(cf. ([33], [19])). With 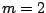 (one boosting step), it has
already been proposed by Tukey ([51]) under the name
''twicing''. In the non-stochastic context, the
(one boosting step), it has
already been proposed by Tukey ([51]) under the name
''twicing''. In the non-stochastic context, the  Boosting
algorithm is known as ''Matching Pursuit'' ([41]) which is
popular in signal processing for fitting overcomplete dictionaries.
Boosting
algorithm is known as ''Matching Pursuit'' ([41]) which is
popular in signal processing for fitting overcomplete dictionaries.
Boosting using the log-likelihood loss for binary classification (and
more generally for multi-class problems) is known as LogitBoost
([34]). LogitBoost uses some Newton-stepping with the Hessian,
rather than the line search in Step 3 of the generic boosting
algorithm:
Step 1 (initialization). Start with
conditional probability estimates
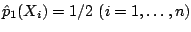 (for
(for
![$ \mathbb{P}[Y=1\vert X = X_i]$](img7256.gif) ). Set
). Set 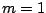 .
.
Step 2. Compute the pseudo-response
(negative gradient)
and the weights
Fit the real-valued base procedure to the current pseudo-response
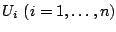 by weighted least squares, using the current
weights
by weighted least squares, using the current
weights
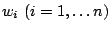 ; the fit is denoted by
; the fit is denoted by
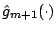 . Update
. Update
and
Step 3 (iteration). Increase iteration
index 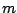 by one and repeat Step 2 until a stopping iteration
by one and repeat Step 2 until a stopping iteration 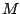 is
achieved.
is
achieved.
The estimate
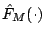 is an estimator for half of
the log-odds ratio
is an estimator for half of
the log-odds ratio
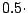 logit
logit![$ (\mathbb{P}[Y=1\vert X=\cdot]$](img7264.gif) (see
Table 16.1). Thus, a classifier (under equal misclassification
loss for the labels
(see
Table 16.1). Thus, a classifier (under equal misclassification
loss for the labels 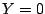 and
and 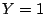 ) is
) is
sign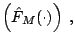 |
|
and an estimate for the conditional probability
![$ \mathbb{P}[Y=1\vert X=\cdot]$](img7266.gif) is
is
A requirement for LogitBoost is that the base procedure has the option
to be fitted by weighted least squares.
The LogitBoost algorithm described above can be modified for
multi-class problems where the response variable takes values in
a finite set
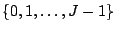 with
with 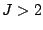 by using the
multinomial log-likelihood loss ([34]). But sometimes it can be
advantageous to run instead a binary classifier (e.g. with boosting)
for many binary problems. The most common approach is to code for
by using the
multinomial log-likelihood loss ([34]). But sometimes it can be
advantageous to run instead a binary classifier (e.g. with boosting)
for many binary problems. The most common approach is to code for 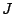 binary problems where the
binary problems where the 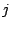 th problem assigns the response
th problem assigns the response
i.e. the so-called ''one versus all'' approach. For example, if
single class-label can be distinguished well from all others, the
''one versus all'' approach seems adequate: empirically, this has
been reported for classifying tumor types based on microarray gene
expressions when using a LogitBoost algorithm ([25]).
Other codings of a multi-class into into multiple binary problems are
discussed in ([1]).
16.3.3 Small Step Size
It is often better to use small step sizes instead of using the full
line search step-length
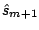 from Step 3 in the generic
boosting algorithm (or
from Step 3 in the generic
boosting algorithm (or
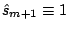 for
for  Boost or
Boost or
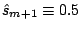 for LogitBoost). We advocate here to use
the step-size
for LogitBoost). We advocate here to use
the step-size
where 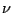 is constant during boosting iterations and small,
e.g.
is constant during boosting iterations and small,
e.g. 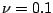 . The parameter
. The parameter 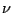 can be seen as a simple
shrinkage parameter, where we use the shrunken
can be seen as a simple
shrinkage parameter, where we use the shrunken
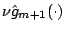 instead of the unshrunken
instead of the unshrunken
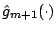 . Small step-sizes (or shrinkage) make the
boosting algorithm slower and require a larger number
. Small step-sizes (or shrinkage) make the
boosting algorithm slower and require a larger number 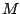 of
iterations. However, the computational slow-down often turns out to be
advantageous for better out-of-sample prediction performance,
(cf. ([33], [19])). There are also some theoretical reasons to
use boosting with
of
iterations. However, the computational slow-down often turns out to be
advantageous for better out-of-sample prediction performance,
(cf. ([33], [19])). There are also some theoretical reasons to
use boosting with 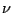 (infinitesimally) small ([29]).
(infinitesimally) small ([29]).
16.3.4 The Bias-variance Trade-off for  Boost
Boost
We discuss here the behavior of boosting in terms of model-complexity
and estimation error when the number of iterations increase. This is
best understood in the framework of squared error loss and
 Boosting.
Boosting.
We represent the base procedure as an operator
which maps a (pseudo-)response vector
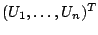 to its
fitted values; the predictor variables
to its
fitted values; the predictor variables 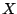 are absorbed here into the
operator notation. That is,
are absorbed here into the
operator notation. That is,
where
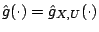 is the estimate from the
base procedure based on data
is the estimate from the
base procedure based on data
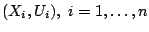 . Then, the
boosting operator in iteration
. Then, the
boosting operator in iteration 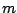 equals
equals
and the fitted values of boosting after 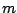 iterations are
iterations are
Heuristically, if the base procedure satisfies
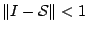 for
a suitable norm, i.e. has a ''learning capacity'' such that the
residual vector is shorter than the input-response vector, we see that
for
a suitable norm, i.e. has a ''learning capacity'' such that the
residual vector is shorter than the input-response vector, we see that
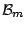 converges to the identity
converges to the identity 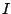 as
as
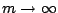 , and
, and
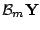 converges to the fully saturated model
converges to the fully saturated model
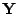 as
as
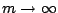 ,
interpolating the response data exactly. Thus, we have to stop the
boosting algorithm at some suitable iteration number
,
interpolating the response data exactly. Thus, we have to stop the
boosting algorithm at some suitable iteration number 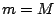 , and we see
that a bias-variance trade-off is involved when varying the iteration
number
, and we see
that a bias-variance trade-off is involved when varying the iteration
number 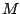 .
.
16.3.5  Boost with Smoothing Spline Base Procedure for
One-dimensional Curve Estimation
Boost with Smoothing Spline Base Procedure for
One-dimensional Curve Estimation
The case where the base procedure is a smoothing spline for
a one-dimensional predictor
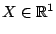 is instructive, although
being only a toy example within the range of potential applications of
boosting algorithms.
is instructive, although
being only a toy example within the range of potential applications of
boosting algorithms.
In our notation from above,
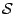 denotes a smoothing spline operator
which is the solution (
denotes a smoothing spline operator
which is the solution (
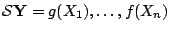 ) of the
following optimization problem (cf. ([54]))
) of the
following optimization problem (cf. ([54]))
The smoothing parameter 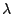 controls the bias-variance
trade-off, and tuning the smoothing spline estimator usually boils
down to estimating a good value of
controls the bias-variance
trade-off, and tuning the smoothing spline estimator usually boils
down to estimating a good value of 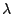 . Alternatively, the
. Alternatively, the
 Boosting approach for curve-estimation with a smoothing spline
base procedure is as follows.
Boosting approach for curve-estimation with a smoothing spline
base procedure is as follows.
Within the class of smoothing spline base procedures, we choose
a spline by fixing a smoothing parameter 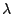 . This should be
done such that the base procedure has low variance but potentially
high bias: for example, we may choose
. This should be
done such that the base procedure has low variance but potentially
high bias: for example, we may choose 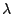 such that the degrees
of freedom
such that the degrees
of freedom
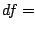 trace
trace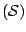 is low, e.g.
is low, e.g. 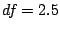 . Although
the base procedure has typically high bias, we will reduce it by
pursuing suitably many boosting iterations. Choosing the
. Although
the base procedure has typically high bias, we will reduce it by
pursuing suitably many boosting iterations. Choosing the 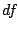 is not
really a tuning parameter: we only have to make sure that
is not
really a tuning parameter: we only have to make sure that 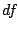 is
small enough, so that the initial estimate (or first few boosting
estimates) are not already overfitting. This is easy to achieve in
practice and a theoretical characterization is described
in ([19]).
is
small enough, so that the initial estimate (or first few boosting
estimates) are not already overfitting. This is easy to achieve in
practice and a theoretical characterization is described
in ([19]).
Related aspects of choosing the base procedure are described in
Sects. 16.3.6 and 16.3.8. The general
''principle'' is to choose a base procedure which has low variance
and having the property that when taking linear combinations thereof,
we obtain a model-class which is rich enough for the application at
hand.
As boosting iterations proceed, the bias of the estimator will go down
and the variance will increase. However, this bias-variance exhibits
a very different behavior as when classically varying the smoothing
parameter (the parameter 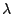 ). It can be shown that the variance
increases with exponentially small increments of the order
). It can be shown that the variance
increases with exponentially small increments of the order
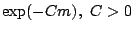 , while the bias decays quickly: the optimal mean
squared error for the best boosting iteration
, while the bias decays quickly: the optimal mean
squared error for the best boosting iteration 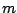 is (essentially) the
same as for the optimally selected tuning parameter
is (essentially) the
same as for the optimally selected tuning parameter 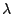 ([19]), but the trace of the mean squared error is very
different, see Fig. 16.4. The
([19]), but the trace of the mean squared error is very
different, see Fig. 16.4. The  Boosting method is much
less sensitive to overfitting and hence often easier to tune. The
mentioned insensitivity about overfitting also applies to
higher-dimensional problems, implying potential advantages about
tuning.
Boosting method is much
less sensitive to overfitting and hence often easier to tune. The
mentioned insensitivity about overfitting also applies to
higher-dimensional problems, implying potential advantages about
tuning.
Figure 16.4:
Mean squared error
![$ \mathbb{E} [(g(X) - \hat {g}(X))^2]$](img206.gif) for
new predictor
for
new predictor 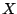 (solid line) and
(solid line) and
![$ n^{-1} \sum _{i=1}^n \mathbb{E}[(\hat {F}_m(X_i) - g(X_i))^2]$](img208.gif) (dotted
line) from 100 simulations of a nonparametric regression model with
smooth regression function and Unif.
(dotted
line) from 100 simulations of a nonparametric regression model with
smooth regression function and Unif.
![$ [-1/2,1/2]$](img209.gif) -distributed design
points. Sample size is
-distributed design
points. Sample size is 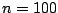 . Left:
. Left:  Boost with cubic smoothing
spline having
Boost with cubic smoothing
spline having 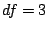 , as a function of boosting itera-
tions
, as a function of boosting itera-
tions 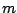 . Right: Cubic smoothing spline for various degrees of
freedom (various amount of smoothing)
. Right: Cubic smoothing spline for various degrees of
freedom (various amount of smoothing)
|
|
Such  Boosting with smoothing splines achieves the asymptotically
optimal minimax MSE rates, and the method can even adapt to higher
order smoothness of the true underlying function, without knowledge of
the true degree of smoothness ([19]).
Boosting with smoothing splines achieves the asymptotically
optimal minimax MSE rates, and the method can even adapt to higher
order smoothness of the true underlying function, without knowledge of
the true degree of smoothness ([19]).
16.3.6  Boost for Additive and Interaction Regression Models
Boost for Additive and Interaction Regression Models
In Sect. 16.3.4, we already pointed out that
 Boosting yields another way of regularization by seeking for
a compromise between bias and variance. This regularization turns out
to be particularly powerful in the context with many predictor
variables.
Boosting yields another way of regularization by seeking for
a compromise between bias and variance. This regularization turns out
to be particularly powerful in the context with many predictor
variables.
Consider the component-wise smoothing spline which is defined as
a smoothing spline with one selected predictor variable
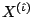 (
(
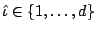 ), where
), where
and
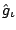 are smoothing splines with single predictors
are smoothing splines with single predictors
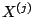 , all having the same low degrees of freedom
, all having the same low degrees of freedom 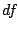 , e.g.
, e.g. 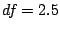 .
.
 Boost with component-wise smoothing splines yields an additive
model, since in every boosting iteration, a function of one selected
predictor variable is linearly added to the current fit and hence, we
can always rearrange the summands to represent the boosting estimator
as an additive function in the original variables,
Boost with component-wise smoothing splines yields an additive
model, since in every boosting iteration, a function of one selected
predictor variable is linearly added to the current fit and hence, we
can always rearrange the summands to represent the boosting estimator
as an additive function in the original variables,
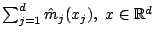 . The estimated functions
. The estimated functions
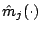 are fitted in a stage-wise fashion and they are
different from the backfitting estimates in additive models
(cf. ([35])). Boosting has much greater flexibility to add
complexity, in a stage-wise fashion: in particular, boosting does
variable selection, since some of the predictors will never be chosen,
and it assigns variable amount of degrees of freedom to the selected
components (or function estimates); the degrees of freedom are defined
below. An illustration of this interesting way to fit additive
regression models with high-dimensional predictors is given in
Figs. 16.5 and 16.6 (actually, a penalized version of
are fitted in a stage-wise fashion and they are
different from the backfitting estimates in additive models
(cf. ([35])). Boosting has much greater flexibility to add
complexity, in a stage-wise fashion: in particular, boosting does
variable selection, since some of the predictors will never be chosen,
and it assigns variable amount of degrees of freedom to the selected
components (or function estimates); the degrees of freedom are defined
below. An illustration of this interesting way to fit additive
regression models with high-dimensional predictors is given in
Figs. 16.5 and 16.6 (actually, a penalized version of
 Boosting, as described below, is shown).
Boosting, as described below, is shown).
When using regression stumps (decision trees having two terminal
nodes) as the base procedure, we also get an additive model fit (by
the same argument as with component-wise smoothing splines). If the
additive terms
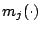 are smooth functions of the predictor
variables, the component-wise smoothing spline is often a better base
procedure than stumps ([19]). For the purpose of
classification, e.g. with LogitBoost, stumps often seem to do a decent
job; also, if the predictor variables are non-continuous,
component-wise smoothing splines are often inadequate.
are smooth functions of the predictor
variables, the component-wise smoothing spline is often a better base
procedure than stumps ([19]). For the purpose of
classification, e.g. with LogitBoost, stumps often seem to do a decent
job; also, if the predictor variables are non-continuous,
component-wise smoothing splines are often inadequate.
Finally, if the number 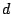 of predictors is ''reasonable'' in
relation to sample size
of predictors is ''reasonable'' in
relation to sample size 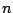 , boosting techniques are not necessarily
better than more classical estimation methods ([19]). It seems
that boosting has most potential when the predictor dimension is very
high ([19]). Presumably, more classical methods become then
very difficult to tune while boosting seems to produce a set of
solutions (for every boosting iteration another solution) whose best
member, chosen e.g. via cross-validation, has often very good
predictive performance. A reason for the efficiency of the trace of
boosting solutions is given in Sect. 16.3.9.
, boosting techniques are not necessarily
better than more classical estimation methods ([19]). It seems
that boosting has most potential when the predictor dimension is very
high ([19]). Presumably, more classical methods become then
very difficult to tune while boosting seems to produce a set of
solutions (for every boosting iteration another solution) whose best
member, chosen e.g. via cross-validation, has often very good
predictive performance. A reason for the efficiency of the trace of
boosting solutions is given in Sect. 16.3.9.
For component-wise base procedures, which pick one or also a pair of
variables at the time, all the component-wise fitting operators are
involved: for simplicity, we focus on additive modeling with
component-wise fitting operators
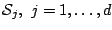 , e.g. the
component-wise smoothing spline.
, e.g. the
component-wise smoothing spline.
The boosting operator, when using the step size
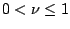 , is
then of the form
, is
then of the form
where
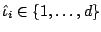 denotes the component which
is picked in the component-wise smoothing spline in the
denotes the component which
is picked in the component-wise smoothing spline in the 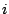 th boosting
iteration.
th boosting
iteration.
If the
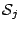 's are all linear operators, and ignoring the effect of
selecting the components, it is reasonable to define the degrees of
boosting as
's are all linear operators, and ignoring the effect of
selecting the components, it is reasonable to define the degrees of
boosting as
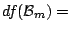 trace trace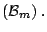 |
|
We can represent
where
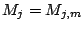 is the linear operator which yields the fitted
values for the
is the linear operator which yields the fitted
values for the 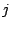 th additive term, e.g.
th additive term, e.g.
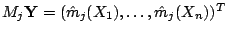 . Note that the
. Note that the 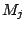 's can
be easily computed in an iterative way by up-dating in the
's can
be easily computed in an iterative way by up-dating in the 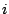 th
boosting iteration as follows:
th
boosting iteration as follows:
and all other
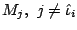 do not change. Thus, we
have a decomposition of the total degrees of freedom into the
do not change. Thus, we
have a decomposition of the total degrees of freedom into the 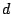 additive terms:
additive terms:
The individual degrees of freedom 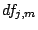 are a useful measure to
quantify the complexity of the
are a useful measure to
quantify the complexity of the 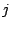 th additive function estimate
th additive function estimate
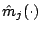 in boosting iteration
in boosting iteration 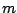 . Note that
. Note that 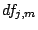 will increase very sub-linearly as a function of boosting
iterations
will increase very sub-linearly as a function of boosting
iterations 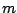 , see also Fig. 16.4.
, see also Fig. 16.4.
Having some degrees of freedom at hand, we can now use the AIC, or
some corrected version thereof, to define a stopping rule of boosting
without doing some sort of cross-validation: the corrected AIC
statistic ([38]) for boosting in the 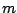 th iteration is
th iteration is
Alternatively, we could use generalized cross-validation
(cf. ([36])), which involves degrees of freedom. This would
exhibit the same computational advantage, as 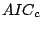 , over
cross-validation: instead of running boosting multiple times,
, over
cross-validation: instead of running boosting multiple times, 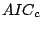 and generalized cross-validation need only one run of boosting (over
a suitable number of iterations).
and generalized cross-validation need only one run of boosting (over
a suitable number of iterations).
When viewing the 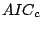 criterion in (16.12) as a reasonable
estimate of the true underlying mean squared error (ignoring
uninteresting constants), we may attempt to construct a boosting
algorithm which reduces in every step the
criterion in (16.12) as a reasonable
estimate of the true underlying mean squared error (ignoring
uninteresting constants), we may attempt to construct a boosting
algorithm which reduces in every step the 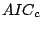 statistic (an
estimate of the out-sample MSE) most, instead of maximally reducing
the in-sample residual sum of squares.
statistic (an
estimate of the out-sample MSE) most, instead of maximally reducing
the in-sample residual sum of squares.
We describe here penalized boosting for additive model fitting using
individual smoothing splines:
Step 1 (initialization). As in Step 1 of
 Boost by fitting a component-wise smoothing spline.
Boost by fitting a component-wise smoothing spline.
Step 2. Compute residuals
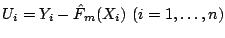 . Choose the individual smoothing
spline which reduces
. Choose the individual smoothing
spline which reduces 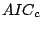 most: denote the selected component by
most: denote the selected component by
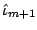 and the fitted function, using the selected
component
and the fitted function, using the selected
component
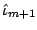 by
by
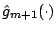 .
.
Update
for some step size
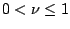 .
.
Step 3 (iteration). Increase iteration
index 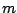 by one and repeat Step 2 until the
by one and repeat Step 2 until the 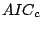 criterion
in (16.12) cannot be improved anymore.
criterion
in (16.12) cannot be improved anymore.
This algorithm cannot be written in terms of fitting a base
procedure multiple times since selecting the component
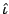 in Step 2 not only depends on the residuals
in Step 2 not only depends on the residuals
 , but
also on the degrees of boosting,
i.e.
trace
, but
also on the degrees of boosting,
i.e.
trace ; the latter is a complicated,
although linear function, of the boosting iterations
; the latter is a complicated,
although linear function, of the boosting iterations
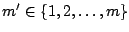 . Penalized
. Penalized  Boost yields more sparse solutions
than the corresponding
Boost yields more sparse solutions
than the corresponding  Boost (with component-wise smoothing
splines as corresponding base procedure). The reason is that
Boost (with component-wise smoothing
splines as corresponding base procedure). The reason is that
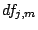 increases only little in iteration
increases only little in iteration 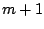 , if the
, if the 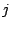 th
selected predictor variables has already been selected many times in
previous iterations; this is directly connected to the slow increase
in variance and overfitting as exemplified in Fig. 16.4.
th
selected predictor variables has already been selected many times in
previous iterations; this is directly connected to the slow increase
in variance and overfitting as exemplified in Fig. 16.4.
An illustration of penalized  Boosting with individual smoothing
splines is shown in Figs. 16.5 and 16.6, based on
simulated data. The simulation model is
Boosting with individual smoothing
splines is shown in Figs. 16.5 and 16.6, based on
simulated data. The simulation model is
where the 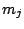 's are smooth curves having varying curve complexities,
as illustrated in Fig. 16.6. Sample size is
's are smooth curves having varying curve complexities,
as illustrated in Fig. 16.6. Sample size is 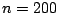 which is
small in comparison to
which is
small in comparison to 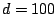 (but the effective number of predictors
is only
(but the effective number of predictors
is only 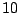 ).
).
Figure 16.5:
Degrees of freedom (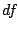 ) in additive model fitting for all
) in additive model fitting for all
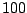 predictor variables (from model (16.14)) during the
process of penalized
predictor variables (from model (16.14)) during the
process of penalized  Boosting with individual smoothing splines
(having
Boosting with individual smoothing splines
(having 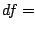 trace
trace
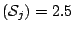 for each spline). The first
ten predictor variables (separated by
the dashed line) are effective.
The result is based on one realization from
model (16.14) with sample size
for each spline). The first
ten predictor variables (separated by
the dashed line) are effective.
The result is based on one realization from
model (16.14) with sample size 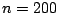 . The plot on the
lower right corresponds to the estimated optimal number of boosting
iterations using the
. The plot on the
lower right corresponds to the estimated optimal number of boosting
iterations using the 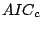 criterion in (16.12). Only three
non-effective predictors have been selected (and assigned small
amount of
criterion in (16.12). Only three
non-effective predictors have been selected (and assigned small
amount of 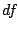 ), and one effective predictor has not been selected
(but whose true underlying function is close to the zero-line, see
Fig. 16.6)
), and one effective predictor has not been selected
(but whose true underlying function is close to the zero-line, see
Fig. 16.6)
|
|
Figure 16.6:
True underlying additive regression curves (dashed lines) and
estimates (solid lines) from penalized  Boosting as described
in Fig. 16.5 (using 436 iterations, estimated from (16.12)). The
last two plots correspond to non-effective predictors (the true
functions are the zero-line), where
Boosting as described
in Fig. 16.5 (using 436 iterations, estimated from (16.12)). The
last two plots correspond to non-effective predictors (the true
functions are the zero-line), where  Boosting assigned most
Boosting assigned most 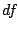 among non-effective predictors
among non-effective predictors
|
|
In terms of prediction performance, penalized  Boosting is not
always better than
Boosting is not
always better than  Boosting; Fig. 16.7 illustrates an
advantage of penalized
Boosting; Fig. 16.7 illustrates an
advantage of penalized  Boosting. But penalized
Boosting. But penalized  Boosting is
always sparser (or at least not less sparse) than the corresponding
Boosting is
always sparser (or at least not less sparse) than the corresponding
 Boosting.
Boosting.
Obviously, penalized  Boosting can be used for other than additive
smoothing spline model fitting. The modifications are straightforward
as long as the individual base procedures are linear operators.
Boosting can be used for other than additive
smoothing spline model fitting. The modifications are straightforward
as long as the individual base procedures are linear operators.
 Boosting for additive modeling can be easily extended to
interaction modeling (having low degree of interaction). Among the
most prominent case is the second order interaction model
Boosting for additive modeling can be easily extended to
interaction modeling (having low degree of interaction). Among the
most prominent case is the second order interaction model
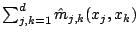 , where
, where
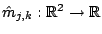 .
.
Boosting with a pairwise thin plate spline, which selects the best
pair of predictor variables yielding lowest residual sum of squares
(when having the same degrees of freedom for every thin plate spline),
yields a second-order interaction model. We demonstrate in
Fig. 16.7 the effectiveness of this procedure in comparison
with the second-order MARS fit ([32]). The underlying model is
the Friedman #1 model:
The sample size is chosen as 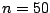 which is small in comparison to
which is small in comparison to
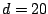 .
.
In high-dimensional settings, it seems that such interaction
 Boosting is clearly better than the more classical MARS fit,
while both of them share the same superb simplicity of interpretation.
Boosting is clearly better than the more classical MARS fit,
while both of them share the same superb simplicity of interpretation.
Figure 16.7:
Mean squared errors for  Boost with pairwise thin-plate splines
(of two predictor variables, having
Boost with pairwise thin-plate splines
(of two predictor variables, having 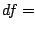 trace
trace
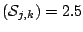 ) (solid lines), its penalized version (dashed lines)
and MARS restricted to the (correct) second order interactions
(dashed/dotted lines). The point with abscissa
) (solid lines), its penalized version (dashed lines)
and MARS restricted to the (correct) second order interactions
(dashed/dotted lines). The point with abscissa 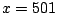 for the
boosting methods corresponds to the performance when estimating the number
of iterations using (16.12). Based on simulated data from
model (16.15) with
for the
boosting methods corresponds to the performance when estimating the number
of iterations using (16.12). Based on simulated data from
model (16.15) with 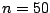
|
|
 Boosting turns out to be also very useful for linear models when
there are many predictor variables. An attractive base procedure is
component-wise linear least squares regression, using the one selected
predictor variables which reduces residual sum of squares most.
Boosting turns out to be also very useful for linear models when
there are many predictor variables. An attractive base procedure is
component-wise linear least squares regression, using the one selected
predictor variables which reduces residual sum of squares most.
This method does variable selection, since some of the predictors will
never be picked during boosting iterations; and it assigns variable
amount of degrees of freedom (or shrinkage), as discussed for additive
models above. Recent theory shows that this method is consistent for
very high-dimensional problems where the number of predictors 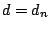 is allowed to grow like
is allowed to grow like
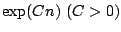 , but the true
underlying regression coefficients are sparse in terms of their
, but the true
underlying regression coefficients are sparse in terms of their
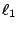 -norm, i.e.
-norm, i.e.
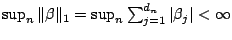 , where
, where 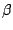 is the vector of regression
coefficients ([16]).
is the vector of regression
coefficients ([16]).
16.3.8 Boosting Trees
The most popular base procedures for boosting, at least in the machine
learning community, are trees. This may be adequate for
classification, but when it comes to regression, or also estimation of
conditional probabilities
![$ \mathbb{P}[Y=1\vert X=x]$](img7353.gif) in classification, smoother
base procedures often perform better if the underlying regression or
probability curve is a smooth function of continuous predictor
variables ([19]).
in classification, smoother
base procedures often perform better if the underlying regression or
probability curve is a smooth function of continuous predictor
variables ([19]).
Even when using trees, the question remains about the size of the
tree. A guiding principle is as follows: take the smallest trees, i.e.
trees with the smallest number 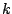 of terminal nodes, such that the
class of linear combinations of
of terminal nodes, such that the
class of linear combinations of 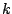 -node trees is sufficiently rich
for the phenomenon to be modeled; of course, there is also here
a trade-off between sample size and the complexity of the function
class.
-node trees is sufficiently rich
for the phenomenon to be modeled; of course, there is also here
a trade-off between sample size and the complexity of the function
class.
For example, when taking stumps with 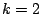 , the set of linear
combinations of stumps is dense in (or ''yields'' the) set of
additive functions ([14]). In ([34]), this is demonstrated
from a more practical point of view. When taking trees with three
terminal nodes (
, the set of linear
combinations of stumps is dense in (or ''yields'' the) set of
additive functions ([14]). In ([34]), this is demonstrated
from a more practical point of view. When taking trees with three
terminal nodes (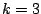 ), the set of linear combinations of 3-node trees
yields all second-order interaction functions. Thus, when aiming for
consistent estimation of the full regression (or conditional
class-probability) function, we should choose trees with
), the set of linear combinations of 3-node trees
yields all second-order interaction functions. Thus, when aiming for
consistent estimation of the full regression (or conditional
class-probability) function, we should choose trees with 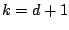 terminal nodes (in practice only if the sample size is
''sufficiently large'' in relation to
terminal nodes (in practice only if the sample size is
''sufficiently large'' in relation to 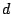 ), (cf. ([14])).
), (cf. ([14])).
Consistency of the AdaBoost algorithm is proved in ([39]),
for example when using trees having 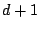 terminal nodes. More
refined results are given in ([42], [55]) for modified
boosting procedures with more general loss functions.
terminal nodes. More
refined results are given in ([42], [55]) for modified
boosting procedures with more general loss functions.
The main disadvantage from a statistical perspective is the lack
of interpretation when boosting trees. This is in sharp contrast
to boosting for linear, additive or interaction modeling. An
approach to enhance interpretation is described in ([33]).
16.3.9 Boosting and 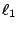 -penalized Methods (Lasso)
-penalized Methods (Lasso)
Another method which does variable selection and variable amount of
shrinkage is basis pursuit ([22]) or Lasso ([50]) which
employs an 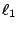 -penalty for the coefficients in the
log-likelihood.
-penalty for the coefficients in the
log-likelihood.
Interestingly, in case of linear least squares regression with a
''positive cone condition'' on the design matrix, an approximate
equivalence of (a version of)  Boosting and Lasso has been
demonstrated in ([29]). More precisely, the set of boosting
solutions, when using an (infinitesimally) small step size (see
Sect. 16.3.3), over all the different boosting
iterations, equals approximately the set of Lasso solutions when
varying the
Boosting and Lasso has been
demonstrated in ([29]). More precisely, the set of boosting
solutions, when using an (infinitesimally) small step size (see
Sect. 16.3.3), over all the different boosting
iterations, equals approximately the set of Lasso solutions when
varying the 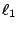 -penalty parameter. Moreover, the approximate set
of boosting solutions can be computed very efficiently by the
so-called least angle regression algorithm ([29]).
-penalty parameter. Moreover, the approximate set
of boosting solutions can be computed very efficiently by the
so-called least angle regression algorithm ([29]).
It is not clear to what extent this approximate equivalence between
boosting and Lasso carries over to more general design matrices in
linear regression or to other problems than regression with other loss
functions. But the approximate equivalence in the above mentioned
special case may help to understand boosting from a different
perspective.
In the machine learning community, there has been a substantial
focus on consistent estimation in the convex hull of function
classes (cf. ([5], [6], [40])). For example,
one may want to estimate a regression or probability function
which can be written as
where the
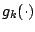 's belong to a function class such as stumps or
trees with a fixed number of terminal nodes. The quantity above is
a convex combination of individual functions, in contrast to boosting
which pursues linear combination of individual functions. By scaling,
which is necessary in practice and theory (cf. ([40])), one can
actually look at this as a linear combination of functions whose
coefficients satisfy
's belong to a function class such as stumps or
trees with a fixed number of terminal nodes. The quantity above is
a convex combination of individual functions, in contrast to boosting
which pursues linear combination of individual functions. By scaling,
which is necessary in practice and theory (cf. ([40])), one can
actually look at this as a linear combination of functions whose
coefficients satisfy
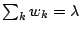 . This then represents an
. This then represents an
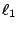 -constraint as in Lasso, a relation which we have already
outlined above.
-constraint as in Lasso, a relation which we have already
outlined above.
Boosting, or functional gradient descent, has also been proposed for
other settings than regression or classification, including survival
analysis ([8]), ordinal response problems ([52]) and
high-multivariate financial time series ([4], [3]).
Support vector machines (cf. ([53], [36], [49])
have become very popular in classification due to their good
performance in a variety of data sets, similarly as boosting
methods for classification. A connection between boosting and
support vector machines has been made in ([46]), suggesting
also a modification of support vector machines to more sparse
solutions ([56]).
Acknowledgements. I would like to thank Marcel Dettling for
some constructive comments.




Next: References
Up: 16. Bagging, Boosting and
Previous: 16.2 Bagging and Related
 Boost
Boost
 -stopping Estimates
-stopping Estimates
 Boosting
Boosting
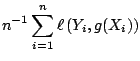
![\includegraphics[height=6.3333cm,width=9cm,clip]{text/3-16/abb/loss.eps}](img7227.gif)
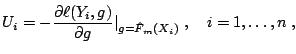
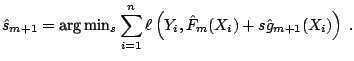
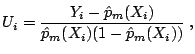
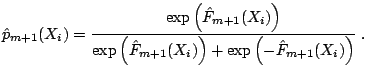
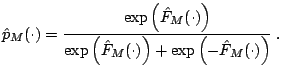
![$\displaystyle Y^{(j)} = \begin{cases}1\;, & \text{if}\;\; Y=j\;,\\ [1.5mm] 0\;, & \text{if}\;\; Y \neq j\;. \end{cases}$](img7270.gif)
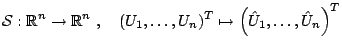
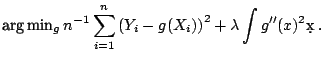
![\includegraphics[height=5.928cm,width=8.3cm]{text/3-16/abb/pbyu.newadd3.eps}](img7296.gif)
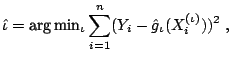
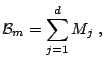
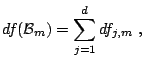
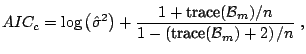
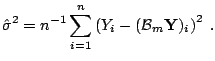
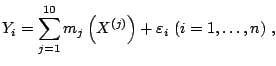
![\includegraphics[width=11.7cm]{text/3-16/abb/boost-dsc2003.2.eps}](img7339.gif)
![\includegraphics[width=11.7cm]{text/3-16/abb/boost-dsc2003.4.eps}](img7340.gif)
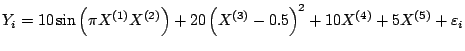
![\includegraphics[height=10cm]{text/3-16/abb/forthfit-dsc2003.eps}](img7349.gif)