![\includegraphics[width=10.2cm]{text/4-1/CSAfin07.eps}](img7567.gif)
|
In response to remarkable regularities discovered by geomorphologists in the 1940s, [4] introduced the hyperbolic law for modeling the grain size distribution of windblown sand. Excellent fits were also obtained for the log-size distribution of diamonds from a large mining area in South West Africa. Almost twenty years later the hyperbolic law was found to provide a very good model for the distributions of daily stock returns from a number of leading German enterprises ([31,57]), giving way to its today's use in stock price modeling ([9]) and market risk measurement ([32]). The name of the distribution is derived from the fact that its log-density forms a hyperbola, see Fig. 1.8. Recall that the log-density of the normal distribution is a parabola. Hence the hyperbolic distribution provides the possibility of modeling heavier tails.
![\includegraphics[width=10.2cm]{text/4-1/CSAfin07.eps}](img7567.gif)
|
The hyperbolic distribution is defined as a normal variance-mean
mixture where the mixing distribution is the generalized inverse
Gaussian (GIG) law with parameter ![]() , i.e. it is
conditionally Gaussian, see [4] and [6]. More
precisely, a random variable
, i.e. it is
conditionally Gaussian, see [4] and [6]. More
precisely, a random variable ![]() has the hyperbolic distribution if:
has the hyperbolic distribution if:
The normalizing constant
K![]() in
formula (1.20) is the modified Bessel function of the
third kind with index
in
formula (1.20) is the modified Bessel function of the
third kind with index ![]() , also known as the MacDonald function.
It is defined as:
, also known as the MacDonald function.
It is defined as:
Relation (1.19) implies that a hyperbolic random variable
![]() H
H![]() can be represented in the
form:
can be represented in the
form:
Sometimes another parameterization of the hyperbolic distribution with
![]() and
and
![]() is used. Then
the probability density function of the hyperbolic
H
is used. Then
the probability density function of the hyperbolic
H![]() law can be written as:
law can be written as:
The hyperbolic law is a member of a more general class of generalized
hyperbolic distributions. The
generalized hyperbolic law can be represented as a normal
variance-mean mixture where the mixing distribution is the generalized
inverse Gaussian (GIG) law with any
![]() . Hence, the
generalized hyperbolic distribution is described by five parameters
. Hence, the
generalized hyperbolic distribution is described by five parameters
![]() . Its probability
density function is given by:
. Its probability
density function is given by:
The normal-inverse Gaussian
(NIG) distributions were introduced by [5] as a subclass of
the generalized hyperbolic laws obtained for
![]() . The
density of the normal-inverse Gaussian distribution is given by:
. The
density of the normal-inverse Gaussian distribution is given by:
At the ''expense'' of four parameters, the NIG distribution is able
to model symmetric and asymmetric distributions with possibly long
tails in both directions. Its tail behavior is often classified as
''semi-heavy'', i.e. the tails are lighter than those of
non-Gaussian stable laws, but much heavier than
Gaussian. Interestingly, if we let ![]() tend to zero the NIG
distribution converges to the Cauchy distribution (with location
parameter
tend to zero the NIG
distribution converges to the Cauchy distribution (with location
parameter ![]() and scale parameter
and scale parameter ![]() ), which exhibits
extremely heavy tails. The tail behavior of the NIG density is
characterized by the following asymptotic relation:
), which exhibits
extremely heavy tails. The tail behavior of the NIG density is
characterized by the following asymptotic relation:
The most natural way of simulating generalized hyperbolic variables stems from the fact that they can be represented as normal variance-mean mixtures. Since the mixing distribution is the generalized inverse Gaussian law, the resulting algorithm reads as follows:
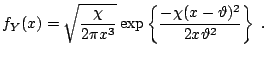 |
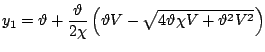 and and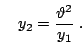 |
In the general case, the GIG distribution - as well as the
(generalized) hyperbolic law - can be simulated via the rejection
algorithm.
An adaptive version of this technique is used to obtain hyperbolic
random numbers in the rhyp function of Rmetrics. Rejection is
also implemented in the HyperbolicDist package for S-plus/R
developed by David Scott, see the R-project home page
http://cran.r-project.org/. The package utilizes a version of the
algorithm proposed by [3], i.e. rejection coupled either
with a two (''GIG algorithm'' for any admissible value of ![]() )
or a three part envelope (''GIGLT1 algorithm'' for
)
or a three part envelope (''GIGLT1 algorithm'' for
![]() ). Envelopes, also called hat or majorizing functions,
provide an upper limit for the PDF of the sampled distribution. The
proper choice of such functions can substantially increase the speed
of computations, see Chap. II.2. As
[3] shows, once the parameter values for these envelopes
have been determined, the algorithm efficiency is reasonable for most
values of the parameter space. However, finding the appropriate
parameters requires optimization and makes the technique burdensome.
). Envelopes, also called hat or majorizing functions,
provide an upper limit for the PDF of the sampled distribution. The
proper choice of such functions can substantially increase the speed
of computations, see Chap. II.2. As
[3] shows, once the parameter values for these envelopes
have been determined, the algorithm efficiency is reasonable for most
values of the parameter space. However, finding the appropriate
parameters requires optimization and makes the technique burdensome.
This difficulty led to a search for a short algorithm which would give
comparable efficiencies but without the drawback of extensive
numerical optimizations. A solution, based on the
''ratio-of-uniforms'' method, was provided a few years later by
[25].
First, recalling properties (1.21)
and (1.22), observe that we only need to find a method
to simulate
![]() GIG
GIG![]() variables and
only for
variables and
only for
![]() . Next, define the relocated variable
. Next, define the relocated variable
![]() , where
, where
![]() is the mode of the density
of
is the mode of the density
of
![]() . Then the relocated variable can be generated by taking
. Then the relocated variable can be generated by taking
![]() , where the pair
, where the pair ![]() is uniformly
distributed over the region
is uniformly
distributed over the region
![]() with:
with:
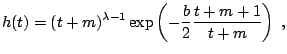 for for |
The parameter estimation of generalized hyperbolic distributions can
be performed by the maximum likelihood method, since there exist
closed-form formulas (although, involving special functions) for the
densities of these laws. The computational burden is not as heavy as
for ![]() -stable laws, but it still is considerable.
-stable laws, but it still is considerable.
In general, the maximum likelihood estimation algorithm is as
follows. For a vector of observations
![]() , the ML
estimate of the parameter vector
, the ML
estimate of the parameter vector
![]() is obtained by maximizing the log-likelihood function:
is obtained by maximizing the log-likelihood function:
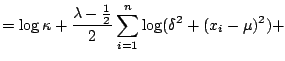 |
||
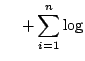 K K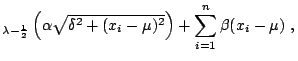 |
(1.36) |
The routines proposed in the literature differ in the choice of the optimization scheme. The first software product that allowed statistical inference with hyperbolic distributions - the HYP program - used a gradient search technique, see [10]. In a large simulation study [84] utilized the bracketing method. The XploRe quantlets mlehyp and mlenig use yet another technique - the downhill simplex method of [77], with slight modifications due to parameter restrictions.
The main factor for the speed of the estimation is the number of
modified Bessel functions to compute. Note, that for
![]() (i.e. the hyperbolic distribution) this function appears only in the
constant
(i.e. the hyperbolic distribution) this function appears only in the
constant ![]() . For a data set with
. For a data set with ![]() independent observations we
need to evaluate
independent observations we
need to evaluate ![]() and
and ![]() Bessel functions for NIG and
generalized hyperbolic distributions, respectively, whereas only one
for the hyperbolic. This leads to a considerable reduction in the time
necessary to calculate the likelihood function in the hyperbolic
case. [84] reported a reduction of ca.
Bessel functions for NIG and
generalized hyperbolic distributions, respectively, whereas only one
for the hyperbolic. This leads to a considerable reduction in the time
necessary to calculate the likelihood function in the hyperbolic
case. [84] reported a reduction of ca. ![]() , however,
the efficiency results are highly sample and implementation
dependent. For example, limited simulation studies performed in XploRe
revealed a
, however,
the efficiency results are highly sample and implementation
dependent. For example, limited simulation studies performed in XploRe
revealed a ![]() ,
, ![]() and
and ![]() reduction in
CPU time for samples of size
reduction in
CPU time for samples of size ![]() ,
, ![]() and
and ![]() , respectively.
, respectively.
We also have to say that the optimization is challenging. Some of the
parameters are hard to separate since a flat-tailed generalized
hyperbolic distribution with a large scale parameter is hard to
distinguish from a fat-tailed distribution with a small scale
parameter, see [6] who observed such a behavior already
for the hyperbolic law. The likelihood function with respect to these
parameters then becomes very flat, and may have local mimima. In the
case of NIG distributions [97] proposed simple estimates
of ![]() and
and ![]() that can be used as staring values for the ML
scheme. Starting from relation (1.34) for the tails of the
NIG density they derived the following approximation:
that can be used as staring values for the ML
scheme. Starting from relation (1.34) for the tails of the
NIG density they derived the following approximation:
Another method of providing the starting values for the ML scheme was
suggested by [84]. He estimated the parameters of a symmetric
(
![]() ) generalized hyperbolic law with a reasonable
kurtosis (i.e. with
) generalized hyperbolic law with a reasonable
kurtosis (i.e. with
![]() ) that had the
variance equal to that of the empirical distribution.
) that had the
variance equal to that of the empirical distribution.
Besides the ML approach other estimation methods have been proposed in
the literature. [84] tested different estimation techniques
by replacing the log-likelihood function with other score functions,
like the Anderson-Darling and Kolmogorov statistics or
![]() -norms. But the results were disappointing. [62] made
use of the Markov chain Monte Carlo technique (see
Chap. II.3), however, again the
results obtained were not impressive. [52] described an EM
type algorithm (see Chap. II.5) for
maximum likelihood estimation of the normal inverse Gaussian
distribution. The algorithm can be programmed in any statistical
package supporting Bessel functions and it has all the properties of
the standard EM algorithm, like sure, but slow, convergence,
parameters in the admissible range, etc. The EM scheme can be also
generalized to the family of generalized hyperbolic distributions.
-norms. But the results were disappointing. [62] made
use of the Markov chain Monte Carlo technique (see
Chap. II.3), however, again the
results obtained were not impressive. [52] described an EM
type algorithm (see Chap. II.5) for
maximum likelihood estimation of the normal inverse Gaussian
distribution. The algorithm can be programmed in any statistical
package supporting Bessel functions and it has all the properties of
the standard EM algorithm, like sure, but slow, convergence,
parameters in the admissible range, etc. The EM scheme can be also
generalized to the family of generalized hyperbolic distributions.
It is always necessary to find a reasonable tradeoff between the introduction of additional parameters and the possible improvement of the fit. [6] mentioned the flatness of the likelihood function for the hyperbolic distribution. The variation in the likelihood function of the generalized hyperbolic distribution is even smaller for a wide range of parameters. Consequently, the generalized hyperbolic distribution applied as a model for financial data leads to overfitting ([84]). In the empirical analysis that follows we will thus concentrate only on NIG distributions. They possess nice analytic properties and have been reported to fit financial data better than hyperbolic laws ([52,62,97]).
| Parameters | ||||
| NIG fit ( |
||||
| Gaussian fit ( |
||||
| Test values | Anderson-Darling | Kolmogorov | ||
| NIG fit | ||||
| Gaussian fit | ||||
| VaR estimates (
|
||||
| Empirical | ||||
| NIG fit | (
|
(
|
||
| Gaussian fit | (
|
(
|
||
Now, we can return to the empirical analysis. This time we want to
check whether DJIA and/or DAX returns can be approximated by the NIG
distribution. We estimate the parameters using the maximum likelihood
approach. As can be seen in Fig. 1.9 the fitted NIG
distribution ''misses'' the very extreme DJIA returns. However, it
seems to give a better fit to the central part of the empirical
distribution than the ![]() -stable law. This is confirmed by
a lower value of the Kolmogorov statistics, compare
Tables 1.2 and 1.4. Surprisingly, also
the Anderson-Darling statistics returns a lower value, implying
a better fit in the tails of the distribution as well.
-stable law. This is confirmed by
a lower value of the Kolmogorov statistics, compare
Tables 1.2 and 1.4. Surprisingly, also
the Anderson-Darling statistics returns a lower value, implying
a better fit in the tails of the distribution as well.
![\includegraphics[width=10.2cm]{text/4-1/CSAfin08.eps}](img7681.gif)
|
In the right panel of Fig. 1.9 we also plotted vertical
lines representing the NIG, Gaussian and empirical daily VaR estimates
at the
![]() and
and ![]() confidence levels. These
estimates correspond to a one day VaR of a virtual portfolio consiting
of one long position in the DJIA index. The NIG
confidence levels. These
estimates correspond to a one day VaR of a virtual portfolio consiting
of one long position in the DJIA index. The NIG ![]() VaR
estimate matches the empirical VaR almost perfectly and the NIG
VaR
estimate matches the empirical VaR almost perfectly and the NIG
![]() VaR estimate also yields a smaller difference than the
stable estimate, compare Tables 1.2
and 1.4. However, if we were interested in very high
confidence levels (i.e. very low quantiles) then the NIG fit would be
less favorable than the stable one. Like in the stable case, no simple
algorithms for inverting the NIG CDF are known but finding the right
quantile could be performed through a binary search routine. For some
members of the generalized hyperbolic family specialized inversion
techniques have been developed. For example,
[59] showed that the approximate inverse of the
hyperbolic CDF can be computed as the solution of a first-order
differential equation.
VaR estimate also yields a smaller difference than the
stable estimate, compare Tables 1.2
and 1.4. However, if we were interested in very high
confidence levels (i.e. very low quantiles) then the NIG fit would be
less favorable than the stable one. Like in the stable case, no simple
algorithms for inverting the NIG CDF are known but finding the right
quantile could be performed through a binary search routine. For some
members of the generalized hyperbolic family specialized inversion
techniques have been developed. For example,
[59] showed that the approximate inverse of the
hyperbolic CDF can be computed as the solution of a first-order
differential equation.
The second analyzed data set comprises ![]() returns of the Deutsche
Aktienindex (DAX) index.
In this case the NIG distribution offers an indisputably better fit
than the Gaussian or even the
returns of the Deutsche
Aktienindex (DAX) index.
In this case the NIG distribution offers an indisputably better fit
than the Gaussian or even the ![]() -stable law, see
Table 1.5 and compare with
Table 1.3. This can be also seen in
Fig. 1.10. The ''drop off'' in the left tail of the
empirical distribution is nicely caught by the NIG distribution. The
empirical VaR estimates are also ''caught'' almost perfectly.
-stable law, see
Table 1.5 and compare with
Table 1.3. This can be also seen in
Fig. 1.10. The ''drop off'' in the left tail of the
empirical distribution is nicely caught by the NIG distribution. The
empirical VaR estimates are also ''caught'' almost perfectly.
| Parameters | ||||
| NIG fit ( |
||||
| Gaussian fit ( |
||||
| Test values | Anderson-Darling | Kolmogorov | ||
| NIG fit | ||||
| Gaussian fit | ||||
| VaR estimates (
|
||||
| Empirical | ||||
| NIG fit | (
|
(
|
||
| Gaussian fit | (
|
(
|
||
![\includegraphics[width=10.2cm]{text/4-1/CSAfin09.eps}](img7692.gif)
|