Stochastic volatility (SV) models
may be used as an alternative to generalized autoregressive conditonal
heteroskedastic (GARCH)
models as a way to model the time-varying
volatility of asset returns. Time series
of asset returns feature stylized facts, the most important being
volatility clustering, which produces a slowly decreasing positive
autocorrelation function of the squared returns, starting at a low
value (about ![]() ). Another stylized fact is excess kurtosis
of the distribution (with respect to the
Gaussian distribution). See [7] for
a detailed list of the stylized facts and a survey of
GARCH models, [47] for a comparative survey of GARCH and
SV models, and [26] for a survey of SV models
focused on their theoretical foundations and their applications in
finance. The first four parts of this section deal with SV models
while in Sect. 2.3.5 we survey similar models for dynamic
duration analysis.
). Another stylized fact is excess kurtosis
of the distribution (with respect to the
Gaussian distribution). See [7] for
a detailed list of the stylized facts and a survey of
GARCH models, [47] for a comparative survey of GARCH and
SV models, and [26] for a survey of SV models
focused on their theoretical foundations and their applications in
finance. The first four parts of this section deal with SV models
while in Sect. 2.3.5 we survey similar models for dynamic
duration analysis.
The simplest version of a SV model is given by
For further use, let ![]() and
and ![]() denote the
denote the ![]() vectors of
observed returns and unobserved log-volatilities, respectively.
vectors of
observed returns and unobserved log-volatilities, respectively.
Estimation of the parameters of the canonical SV model
may be done by the
maximum likelihood (ML)
method or by
Bayesian inference. Other methods have been used but they will not be
considered here. We refer to [26], Sect. 5,
for a review. ML and, in principle, Bayesian estimation require to
compute the likelihood function
of an observed sample, which is a difficult task. Indeed, the density
of ![]() given
given
![]() and an initial condition
and an initial condition ![]() (not
explicitly written in the following expressions) requires to compute
a multiple integral
which has a dimension equal to the sample size:
(not
explicitly written in the following expressions) requires to compute
a multiple integral
which has a dimension equal to the sample size:
Two methods directly approximate (2.22):
efficient importance sampling (EIS), and
Monte Carlo
maximum likelihood (MCML). Another approach, which can only be used
for
Bayesian inference, works with
![]() as data density, and
produces a posterior joint density for
as data density, and
produces a posterior joint density for
![]() given
given
![]() . The posterior density
is simulated by a
Monte Carlo Markov chain (MCMC)
algorithm, which produces simulated values of
. The posterior density
is simulated by a
Monte Carlo Markov chain (MCMC)
algorithm, which produces simulated values of
![]() and
and
![]() . Posterior moments and marginal densities of
. Posterior moments and marginal densities of
![]() are then estimated by their simulated sample
counterparts. We pursue by describing each method.
are then estimated by their simulated sample
counterparts. We pursue by describing each method.
A look at (2.23) suggests to sample ![]() sequences
sequences
![]() ,
,
![]() , and to
approximate it by
, and to
approximate it by
![]() . This direct method proves to be
inefficient. Intuitively, the sampled sequences of
. This direct method proves to be
inefficient. Intuitively, the sampled sequences of ![]() are not
linked to the observations
are not
linked to the observations ![]() . To improve upon this, the
integral (2.22), which is the convenient expression to present
EIS, is expressed as
. To improve upon this, the
integral (2.22), which is the convenient expression to present
EIS, is expressed as
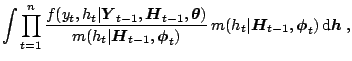 |
(2.24) |
A convenient choice for ![]() is the Gaussian family of distributions.
A Gaussian approximation to
is the Gaussian family of distributions.
A Gaussian approximation to ![]() , as a function of
, as a function of ![]() , given
, given ![]() and
and ![]() , turns out to be efficient. It can be expressed as
proportional to
, turns out to be efficient. It can be expressed as
proportional to
![]() , where
, where
![]() , the auxiliary
parameters. It is convenient to multiply it with
, the auxiliary
parameters. It is convenient to multiply it with
![]() 0.5
0.5
![]() , where
, where
![]() , which comes from the
, which comes from the
![]() term included in
term included in
![]() . The
product of these two exponential functions can be expressed as
a Gaussian density
. The
product of these two exponential functions can be expressed as
a Gaussian density
![]() , where
, where
| (2.26) |
The choice of the auxiliary parameters can be split into ![]() separate
problems, one for each
separate
problems, one for each ![]() . It amounts to minimize the sum of squared
deviations between
. It amounts to minimize the sum of squared
deviations between
![]() plus
a correction term, see (2.27), and
plus
a correction term, see (2.27), and
![]() where
where
![]() is
an auxiliary intercept term. This problem is easily solved by
ordinary least squares. See [36] for a detailed
explanation.
is
an auxiliary intercept term. This problem is easily solved by
ordinary least squares. See [36] for a detailed
explanation.
Let us summarize the core of the EIS
algorithm in three steps (for given
![]() and
and ![]() ):
):
Step 1: Generate ![]() trajectories
trajectories ![]() using
the `natural' samplers
using
the `natural' samplers
![]() .
.
Step 2: For each ![]() (starting from
(starting from ![]() and
ending at
and
ending at ![]() ), using the
), using the ![]() observations generated in the previous
step, estimate by OLS
the regression
observations generated in the previous
step, estimate by OLS
the regression
Step 3: Generate ![]() trajectories
trajectories ![]() using
the efficient samplers
using
the efficient samplers
![]() and finally
compute (2.25).
and finally
compute (2.25).
Steps 1 to 3 should be iterated about five times to improve the
efficiency of the approximations. This is done by replacing the
natural sampler in Step 1 by the importance functions
built in the previous iteration. It is also possible to start Step 1
of the first iteration with a more efficient sampler than the natural
one. This is achieved by multiplying the natural sampler by a normal
approximation to
![]() 0.5
0.5
![]() . The normal approximation is based on
a second-order Taylor series expansion of the argument of the
exponential in the previous expression around
. The normal approximation is based on
a second-order Taylor series expansion of the argument of the
exponential in the previous expression around ![]() . In this way,
the initial importance sampler links
. In this way,
the initial importance sampler links ![]() and
and ![]() . This enables one
to reduce to three (instead of five) the number of iterations over the
three steps. In practical implementations,
. This enables one
to reduce to three (instead of five) the number of iterations over the
three steps. In practical implementations, ![]() can be fixed
to
can be fixed
to ![]() . When computing (2.25) for different values
of
. When computing (2.25) for different values
of ![]() , such as in a numerical
optimizer, it is important to use common random numbers
to generate the set of
, such as in a numerical
optimizer, it is important to use common random numbers
to generate the set of ![]() trajectories
trajectories ![]() that serve in the
computations.
that serve in the
computations.
It is also easy to compute by EIS
filtered estimates of functions of ![]() , such as the conditional
standard deviation
, such as the conditional
standard deviation
![]() , conditional on the past returns (but
not on the lagged unobserved
, conditional on the past returns (but
not on the lagged unobserved ![]() ), given a value of
), given a value of
![]() (such as the ML estimate). Diagnostics on the model
specification are then obtained as a byproduct: if the model is
correctly specified,
(such as the ML estimate). Diagnostics on the model
specification are then obtained as a byproduct: if the model is
correctly specified, ![]() divided by the filtered estimates of
divided by the filtered estimates of
![]() is a residual that has zero mean, unit variance, and is
serially uncorrelated (this also holds for the squared residual).
is a residual that has zero mean, unit variance, and is
serially uncorrelated (this also holds for the squared residual).
[43] contains a general presentation of EIS and its properties.
The likelihood
to be computed at
![]() (the data) and any given
(the data) and any given
![]() is equal to
is equal to
![]() and is
conveniently expressed as (2.21) for this method. This quantity
is approximated by importance sampling
with an
importance function defined from an approximating model. The latter is
obtained by using the state space
representation of the canonical SV model
(parametrized with
and is
conveniently expressed as (2.21) for this method. This quantity
is approximated by importance sampling
with an
importance function defined from an approximating model. The latter is
obtained by using the state space
representation of the canonical SV model
(parametrized with ![]() ):
):
In brief, the likelihood function is approximated by
For SML
estimation, the approximation in (2.32) is transformed in
logarithm. This induces a bias since the expectation of the log of the
sample mean is not the log of the corresponding integral
in (2.31). The bias is corrected by adding
![]() to the log of (2.32), where
to the log of (2.32), where ![]() is the sample variance of
the ratios
is the sample variance of
the ratios
![]() and
and ![]() is the sample mean of the same ratios, i.e.
is the sample mean of the same ratios, i.e. ![]() is
the sample mean appearing in (2.32). Moreover,
[20] use
antithetic and
control variables to improve the efficiency of the estimator of the
log-likelihood function.
is
the sample mean appearing in (2.32). Moreover,
[20] use
antithetic and
control variables to improve the efficiency of the estimator of the
log-likelihood function.
[21] present several generalizations of MCML (e.g. the case where the state variable in non-Gaussian) and develop analogous methods for Bayesian inference.
We present briefly the
`Mixture Sampler', one of the three algorithms added by
[35] to the six algorithms already in the
literature at that time (see their paper for references). They
approximate the density of
![]() by
a finite mixture
of seven Gaussian densities, such that in particular the first four
moments of both densities are equal. The approximating density can be
written as
by
a finite mixture
of seven Gaussian densities, such that in particular the first four
moments of both densities are equal. The approximating density can be
written as
The crux of the algorithm is to add
![]() to
to
![]() and
and
![]() in the MCMC
sampling space. This makes it possible to sample
in the MCMC
sampling space. This makes it possible to sample
![]() ,
,
![]() and
and
![]() within
a Gibbs sampling algorithm. Remark that
within
a Gibbs sampling algorithm. Remark that
![]() and
and
![]() are independent given
are independent given
![]() and
and
![]() . Moreover,
. Moreover,
![]() can be sampled entirely as
a vector. The intuition behind this property is that, once
can be sampled entirely as
a vector. The intuition behind this property is that, once
![]() is known, the relevant term of the mixture (2.33) is
known for each observation, and since this is
a Gaussian density, the whole apparatus of the
Kalman filter can be used. Actually, this a bit more involved since
the relevant
Gaussian density depends on
is known, the relevant term of the mixture (2.33) is
known for each observation, and since this is
a Gaussian density, the whole apparatus of the
Kalman filter can be used. Actually, this a bit more involved since
the relevant
Gaussian density depends on ![]() , but an augmented Kalman filter
is available for this case.
, but an augmented Kalman filter
is available for this case.
Sampling
![]() as one block is a big progress over previous
algorithms, such as in [33], where each
element
as one block is a big progress over previous
algorithms, such as in [33], where each
element ![]() is sampled individually given the other elements of
is sampled individually given the other elements of
![]() (plus
(plus
![]() and
and
![]() ). The slow
convergence of such algorithms is due to the high correlations between
the elements of
). The slow
convergence of such algorithms is due to the high correlations between
the elements of
![]() .
.
[35] write the model in state space
form, using ![]() rather than
rather than ![]() or
or ![]() as a parameter, i.e.
as a parameter, i.e.
[35] also propose an algorithm to compute
filtered estimates of ![]() , from which model diagnostics can be
obtained as described above for EIS.
, from which model diagnostics can be
obtained as described above for EIS.
For illustration, estimates of the
canonical SV model parameters are reported in Table 2.8 for
a series of ![]() centred daily returns of the Standard and
Poor's 500 (SP500) composite price index (period:
02/01/80-30/05/03, source: Datastream). Returns are computed
as 100 times the log of the price ratios. The sample mean and standard
deviation are equal to
centred daily returns of the Standard and
Poor's 500 (SP500) composite price index (period:
02/01/80-30/05/03, source: Datastream). Returns are computed
as 100 times the log of the price ratios. The sample mean and standard
deviation are equal to ![]() and
and ![]() , respectively.
, respectively.
| EIS ( |
MCML ( |
MCMC ( |
||||
|
|
( |
( |
( |
|||
| ( |
( |
( |
||||
| ( |
( |
( |
||||
| llf | ||||||
| Time | 2.36 min | 7.56 min | 6.23 min | |||
| Code | Gauss | Ox | Ox | |||
We used computer codes provided by the authors cited above. For EIS, we received the code from R. Liesenfeld, for MCML and MCMC we downloaded them from the web site staff.feweb.vu.nl/koopman/sv.
For
SML estimation by
EIS
or
MCML, identical initial values (
![]() ,
,
![]() ,
,
![]() or
or ![]() ) and
optimization algorithms (BFGS)
are used, but in different programming environments. Therefore, the
computing times are not fully comparable, although a careful rule of
thumb is that Ox is two to three times faster than Gauss (see
[15]). Reported execution times imply that EIS
appears to be at least six times faster than MCML. This is a reversal
of a result reported by Sandman and Koopman (1998, p.289), but they
compared MCML with a precursor of EIS
implemented by [16]. More importantly, the two methods
deliver quasi-identical results.
) and
optimization algorithms (BFGS)
are used, but in different programming environments. Therefore, the
computing times are not fully comparable, although a careful rule of
thumb is that Ox is two to three times faster than Gauss (see
[15]). Reported execution times imply that EIS
appears to be at least six times faster than MCML. This is a reversal
of a result reported by Sandman and Koopman (1998, p.289), but they
compared MCML with a precursor of EIS
implemented by [16]. More importantly, the two methods
deliver quasi-identical results.
MCMC
results
are based on ![]() draws after dropping
draws after dropping ![]() initial
draws. The posterior means
and standard deviations are also quite close to the ML results. The
posterior density
of
initial
draws. The posterior means
and standard deviations are also quite close to the ML results. The
posterior density
of ![]() (computed by
kernel estimation) is shown in Fig. 2.1 together with the
large sample normal approximation to the density of the ML estimator
using the EIS
results. The execution time for
MCMC is
difficult to compare with the other methods since it depends on the
number of Monte Carlo draws. It is however quite competitive since
reliable results are obtained in no more time than
MCML
in this example.
(computed by
kernel estimation) is shown in Fig. 2.1 together with the
large sample normal approximation to the density of the ML estimator
using the EIS
results. The execution time for
MCMC is
difficult to compare with the other methods since it depends on the
number of Monte Carlo draws. It is however quite competitive since
reliable results are obtained in no more time than
MCML
in this example.
The canonical model presented in (2.19) is too restrictive to fit
the excess kurtosis
of many return series. Typically, the residuals of the model reveal
that the distribution of ![]() has fatter tails than the
Gaussian distribution. The assumption of normality is most often
replaced by the assumption that
has fatter tails than the
Gaussian distribution. The assumption of normality is most often
replaced by the assumption that
![]() , which denotes
Student-
, which denotes
Student-![]() distribution
with zero mean, unit variance, and degrees of freedom parameter
distribution
with zero mean, unit variance, and degrees of freedom parameter
![]() . SML
estimates of
. SML
estimates of ![]() are usually between
are usually between ![]() and
and ![]() for stock and
foreign currency returns using daily data. Posterior means
are larger because the posterior density
of has a long tail to the right.
for stock and
foreign currency returns using daily data. Posterior means
are larger because the posterior density
of has a long tail to the right.
Several other extensions of the simple SV model presented
in (2.19) exist in the literature. The mean of ![]() need not be
zero and may be a function of explanatory variables
need not be
zero and may be a function of explanatory variables ![]() (often a lag
of
(often a lag
of ![]() and an intercept term). Similarly
and an intercept term). Similarly ![]() may be a function of
observable variables (
may be a function of
observable variables (![]() ) in addition to its own lags. An extended
model along these lines is
) in addition to its own lags. An extended
model along these lines is
It should be obvious that all these extensions are very easy to incorporate in EIS (see [36]) and MCML (see [46]). Bayesian estimation by MCMC remains quite usable but becomes more demanding in research time to tailor the algorithm for achieving a good level of efficiency of the Markov chain (see [12], in particular p 301-302, for such comments).
[12] also include a jump component term ![]() in the conditional mean part to allow for irregular, transient
movements in returns. The random variable
in the conditional mean part to allow for irregular, transient
movements in returns. The random variable ![]() is equal to
is equal to ![]() with
unknown probablity
with
unknown probablity ![]() and zero with probability
and zero with probability ![]() ,
whereas
,
whereas ![]() is the size of the jump when it occurs. These
time-varying jump sizes are assumed independent draws of
is the size of the jump when it occurs. These
time-varying jump sizes are assumed independent draws of
![]() 0.5
0.5
![]() ,
, ![]() being an unknown
parameter representing the standard deviation of the jump size. For
daily SP500 returns (period: 03/07/1962-26/08/1997) and
a Student-
being an unknown
parameter representing the standard deviation of the jump size. For
daily SP500 returns (period: 03/07/1962-26/08/1997) and
a Student-![]() density for
density for ![]() , [12] report
posterior means of
, [12] report
posterior means of ![]() for
for ![]() , and
, and ![]() for
for ![]() (for prior means of
(for prior means of ![]() and
and ![]() ,
respectively). This implies that a jump occurs on average every
,
respectively). This implies that a jump occurs on average every
![]() days, and that the variability of the jump size is on average
days, and that the variability of the jump size is on average
![]() . They also find that the removal of the jump component
from the model reduces the
posterior mean of
. They also find that the removal of the jump component
from the model reduces the
posterior mean of ![]() from
from ![]() to
to ![]() , which corresponds to the
fact that the jumps capture some
outliers.
, which corresponds to the
fact that the jumps capture some
outliers.
Another extension consists of relaxing the restriction of zero
correlation ![]() between
between ![]() and
and ![]() . This may be useful for
stock returns for which a negative correlation corresponds to the
leverage effect of the financial literature. If the correlation is
negative, a drop of
. This may be useful for
stock returns for which a negative correlation corresponds to the
leverage effect of the financial literature. If the correlation is
negative, a drop of ![]() , interpreted as a negative shock on the
return, tends to increase
, interpreted as a negative shock on the
return, tends to increase ![]() and therefore
and therefore ![]() . Hence volatility
increases more after a negative shock than after a positive shock of
the same absolute value, which is a well-known stylized
fact. [46] estimate such
a model by
MCML, and report
. Hence volatility
increases more after a negative shock than after a positive shock of
the same absolute value, which is a well-known stylized
fact. [46] estimate such
a model by
MCML, and report
![]() for daily returns of the
SP500 index (period: 02/01/80-30/12/87), while
[34] do it by
Bayesian inference using
MCMC
and report
a posterior mean of
for daily returns of the
SP500 index (period: 02/01/80-30/12/87), while
[34] do it by
Bayesian inference using
MCMC
and report
a posterior mean of ![]() equal to
equal to ![]() on the same
data. They use the same reparametrization as in (2.13) to impose
that the first diagonal element of the covariance matrix of
on the same
data. They use the same reparametrization as in (2.13) to impose
that the first diagonal element of the covariance matrix of ![]() and
and
![]() must be equal to
must be equal to ![]() . This covariance matrix is given by
. This covariance matrix is given by
Multivariate SV models are also on the agenda of researchers. [36] estimate by EIS a one-factor model introduced by [47], using return series of four currencies. [35], Sect. 6.6, explain how to deal with the multi-factor model case by extending the MCMC algorithm reviewed in Sect. 2.3.2.
Models akin to the SV model have been used for dynamic duration analysis by [5] and [3]. The context of application is the analysis of a sequence of time spells between events (also called durations) occurring on stock trading systems like the New York Stock Exchange (NYSE). Time stamps of trades are recorded for each stock on the market during trading hours every day, resulting in an ordered series of durations. Marks, such as the price, the exchanged quantity, the prevailing bid and ask prices, and other observed features may also be available, enabling to relate the durations to the marks in a statistical model. See [2] for a presentation of the issues.
Let
![]() denote the arrival times and
denote the arrival times and
![]() denote the corresponding durations, i.e.
denote the corresponding durations, i.e.
![]() . The
stochastic conditional duration (SCD) model of
[5] is defined as
. The
stochastic conditional duration (SCD) model of
[5] is defined as
The similarity with the canonical SV
model (2.19) is striking. A major difference is the non-normality
of ![]() since this is by definition a positive random variable. This
feature makes it possible to identify
since this is by definition a positive random variable. This
feature makes it possible to identify ![]() . Therefore, the
estimation methods available for the SV model can be adapted to the
estimation of
SCD models. [5] have estimated the SCD model by
the quasi-maximum likelihood (QML)
method, since the first equation of the model may be expressed as
. Therefore, the
estimation methods available for the SV model can be adapted to the
estimation of
SCD models. [5] have estimated the SCD model by
the quasi-maximum likelihood (QML)
method, since the first equation of the model may be expressed as
![]() . If
. If ![]() were
Gaussian, the model would be a Gaussian linear state space model
and the Kalman filter
could be directly applied. QML relies on maximizing the likelihood
function
as if
were
Gaussian, the model would be a Gaussian linear state space model
and the Kalman filter
could be directly applied. QML relies on maximizing the likelihood
function
as if ![]() were Gaussian. The QML
estimator is known to be consistent but inefficient relative to the ML
estimator which would obtain if the correct distribution of
were Gaussian. The QML
estimator is known to be consistent but inefficient relative to the ML
estimator which would obtain if the correct distribution of ![]() were used to define the
likelihood function. [24], Chap. 3, has studied by
simulation
the loss of efficiency of QML relative to ML. ML estimation assuming
a Weibull distribution
is done by applying the
EIS algorithm. For a sample size of
were used to define the
likelihood function. [24], Chap. 3, has studied by
simulation
the loss of efficiency of QML relative to ML. ML estimation assuming
a Weibull distribution
is done by applying the
EIS algorithm. For a sample size of ![]() observations, the efficiency
loss ranges from
observations, the efficiency
loss ranges from ![]() to
to ![]() , except for the
parameter
, except for the
parameter ![]() , for which it is very small. He also applied the
EIS method using the same data as in [5]. For
example, for a dataset of
, for which it is very small. He also applied the
EIS method using the same data as in [5]. For
example, for a dataset of ![]() volume durations of the Boeing
stock (period: September-November 1996; source: TAQ database
of
NYSE), the ML estimates are:
volume durations of the Boeing
stock (period: September-November 1996; source: TAQ database
of
NYSE), the ML estimates are:
![]() ,
,
![]() ,
,
![]() ,
,
![]() . They imply a high persistence in the conditional mean
process (corresponding to duration clustering),
a Weibull distribution
with an increasing concave
hazard function, and substantial
heterogeneity. Notice that an interesting feature of the SCD model
is that the distribution of
. They imply a high persistence in the conditional mean
process (corresponding to duration clustering),
a Weibull distribution
with an increasing concave
hazard function, and substantial
heterogeneity. Notice that an interesting feature of the SCD model
is that the distribution of ![]() conditional to the past information,
but marginalized with respect to the latent process, is a Weibull
mixed by a lognormal
distribution.
conditional to the past information,
but marginalized with respect to the latent process, is a Weibull
mixed by a lognormal
distribution.
[48] have designed
a MCMC
algorithm for the
SCD model (2.38) assuming a standard exponential distribution
for ![]() . The design of their MCMC algorithm borrows features from
Koopman and Durbin's MCML approach
and one of the MCMC algorithms used for the
SV model.
. The design of their MCMC algorithm borrows features from
Koopman and Durbin's MCML approach
and one of the MCMC algorithms used for the
SV model.
As an alternative to modelling the sequence of durations, [3] model directly the arrival times through the intensity function of the point process. Their model specifies a dynamic intensity function, where the intensity function is the product of two intensity components: an observable component that depends on past arrival times, and a latent component. The logarithm of the latter is a Gaussian autoregressive process similar to the second equation in (2.19) and (2.38). The observable component may be a Hawkes process ([31]) or an autoregressive intensity model ([45]). When the model is multivariate, there is an observable intensity component specific to each particular point process, while the latent component is common to all particular processes. Interactions between the processes occur through the observable components and through the common component. The latter induces similar dynamics in the particular processes, reflecting the impact of a common factor influencing all processes. Bauwens and Hautsch use intensity-based likelihood inference, with the EIS algorithm to deal with the latent component.