Many econometric isuues require models that are richer or more flexible than the conventional regression type models. Several possibilities exist. For example, as explained in Sect. 2.2.3, the logit model is made more realistic by generalizing it to a mixed logit. Many models currently used in econometrics can be generalized in such a way.
In this section, we assume that the univariate or multivariate
observations
![]() are considered as draws of
are considered as draws of
The structure of (2.39) implies that the likelihood
for all the ![]() observations contains
observations contains ![]() terms
terms
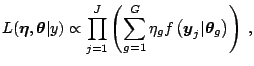 |
(2.40) |
Bayesian inference
on finite mixture
distributions by
MCMC
sampling is explained in [19]. Gibbs sampling
on
![]() is difficult since the posterior
distributions of
is difficult since the posterior
distributions of
![]() and
and
![]() are generally unknown. For
the same reason as for the probit model
in Sect. 2.2.1 and the stochastic volatility model in
Sect. 2.3, inference on the finite mixture model
is straightforward once the state or group of an observation is
known. Data augmentation
is therefore an appropriate way to render inference easier. Define the
state indicator
are generally unknown. For
the same reason as for the probit model
in Sect. 2.2.1 and the stochastic volatility model in
Sect. 2.3, inference on the finite mixture model
is straightforward once the state or group of an observation is
known. Data augmentation
is therefore an appropriate way to render inference easier. Define the
state indicator ![]() which takes value
which takes value ![]() when
when
![]() belongs to state or group
belongs to state or group ![]() where
where
![]() . Denote by
. Denote by
![]() the
the ![]() -dimensional discrete vector containing all the
state indicators. To facilitate the inference, prior independence,
that is
-dimensional discrete vector containing all the
state indicators. To facilitate the inference, prior independence,
that is
![]() , is
usually imposed. As shown in the next examples, the posterior
distributions
, is
usually imposed. As shown in the next examples, the posterior
distributions
![]() ,
,
![]() and
and
![]() are either
known distributions easy to sample from or they are distributions for
which a second, but simpler, MCMC
sampler
is set up. A Gibbs sampler
with three main blocks may therefore be used.
are either
known distributions easy to sample from or they are distributions for
which a second, but simpler, MCMC
sampler
is set up. A Gibbs sampler
with three main blocks may therefore be used.
The complete data likelihood
of the finite mixture
is invariant to a relabeling of the states. This means that we can
take the labeling
![]() and do a permutation
and do a permutation
![]() without changing the value of the likelihood
function. If the prior
is also invariant to relabeling then the posterior has this property
also. As a result, the posterior has potentially
without changing the value of the likelihood
function. If the prior
is also invariant to relabeling then the posterior has this property
also. As a result, the posterior has potentially ![]() different
modes. To solve this identification
or label switching problem, identification restrictions
have to be imposed.
different
modes. To solve this identification
or label switching problem, identification restrictions
have to be imposed.
Note that the inference described here is conditional on ![]() , the
number of components. There are two modelling approaches to take care
of
, the
number of components. There are two modelling approaches to take care
of ![]() . First, one can treat
. First, one can treat ![]() as an extra parameter in the model as
is done in [44] who make use of the reversible
jump
MCMC
methods. In this way, the prior information on the number of
components can be taken explicitly into account by specifying for
example
a Poisson distribution on
as an extra parameter in the model as
is done in [44] who make use of the reversible
jump
MCMC
methods. In this way, the prior information on the number of
components can be taken explicitly into account by specifying for
example
a Poisson distribution on ![]() in such a way that it favors a small
number of components. A second approach is to treat the choice of
in such a way that it favors a small
number of components. A second approach is to treat the choice of ![]() as a problem of
model selection. By so-doing one separates the issue of the choice of
as a problem of
model selection. By so-doing one separates the issue of the choice of
![]() from estimation with
from estimation with ![]() fixed. For example, one can take
fixed. For example, one can take ![]() and
and ![]() and do the estimation separately for the two models. Then
Bayesian model comparison techniques (see
Chap. III.11) can be applied, for
instance by the calculation of the
Bayes factor, see [14] and [9] for more
details.
and do the estimation separately for the two models. Then
Bayesian model comparison techniques (see
Chap. III.11) can be applied, for
instance by the calculation of the
Bayes factor, see [14] and [9] for more
details.
We review two examples. The first example fits US quarterly GNP data using a Markov switching autoregressive model. The second example is about the clustering of many GARCH models.
[23] uses US quarterly real GNP growth data from 1951:2 to 1984:4. This series was initially used by [30] and is displayed in Fig. 2.2. The argument is that contracting and expanding periods are generated by the same model but with different parameters. These models are called state- (or regime-) switching models.
After some investigation using Bayesian model selection techniques, the adequate specification for the US growth data is found to be the two-state switching AR(2) model
In the second step, this sample is used to identify the model. This is done by visual inspection of the posterior marginal and bivariate densities. Identification restrictions need to be imposed to avoid multimodality of the posterior densities. Once suitable restrictions are found, a final MCMC sample is constructed to obtain the moments of the constrained posterior density. The latter sample is constructed by permutation sampling under the restrictions, which means that (2) is replaced by one permutation defining the constrained parameter space.
In the GNP growth data example, two identification restrictions
seem possible, namely
![]() and
and
![]() , see [23] for
details. Table 2.9 provides the
posterior means and standard deviations of the
, see [23] for
details. Table 2.9 provides the
posterior means and standard deviations of the
![]() 's for
both identification
restrictions.
's for
both identification
restrictions.
|
|
|
|||
| Contraction | Expansion | Contraction | Expansion | |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
||
The GNP growth in contraction and expansion periods not only have different unconditional means, they are also driven by different dynamics. Both identification restrictions result in similar posterior moments.
[4] focus on the differentiation between the
component distributions via different conditional heteroskedasticity
structures by the use of GARCH models. In this framework, the
observation ![]() is multivariate and the
is multivariate and the
![]() 's are
the parameters of GARCH(1,1) models. The purpose is to estimate many,
of the order of several hundreds, GARCH models. Each financial time
series
belongs to one of the
's are
the parameters of GARCH(1,1) models. The purpose is to estimate many,
of the order of several hundreds, GARCH models. Each financial time
series
belongs to one of the ![]() groups but it is not known a priori which
series belongs to which cluster.
groups but it is not known a priori which
series belongs to which cluster.
An additional identification
problem arises due to the possibility of empty groups. If a group is
empty then the posterior of
![]() is equal to the prior
of
is equal to the prior
of
![]() . Therefore an improper prior is not allowed for
. Therefore an improper prior is not allowed for
![]() . The identification
problems are solved by using an informative prior
on each
. The identification
problems are solved by using an informative prior
on each
![]() . The identification restrictions use the
fact that we work with GARCH
models: we select rather non-overlapping supports for the parameters,
such that the prior
. The identification restrictions use the
fact that we work with GARCH
models: we select rather non-overlapping supports for the parameters,
such that the prior
![]() depends on a labeling choice. Uniform prior
densities on each parameter, on finite intervals, possibly subject to
stationarity restrictions, are relatively easy to specify.
depends on a labeling choice. Uniform prior
densities on each parameter, on finite intervals, possibly subject to
stationarity restrictions, are relatively easy to specify.
Bayesian inference is done by use of the Gibbs sampler and data augmentation. Table 2.10 summarizes the three blocks of the sampler.
Because of the prior independence of the
![]() 's, the
griddy-Gibbs sampler is applied separately
's, the
griddy-Gibbs sampler is applied separately ![]() times.
times.
| True value | |||
| Mean | |||
| Standard deviation | |||
| Correlation matrix | |||
| True value | ||||
| Prior interval | ||||
| Mean | ||||
| Standard deviation | ||||
| Correlation |
|
As an illustration we show the posterior marginals of the following model
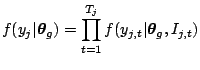 |
(2.43) |
| (2.44) | |
| (2.45) |
[4] succesfully apply this model to return
series of 131 US stocks. Comparing the marginal likelihoods
for different models, they find that ![]() is the appropriate choice
for the number of component distributions.
is the appropriate choice
for the number of component distributions.
Other interesting examples of finite mixture modelling exist in the literature. [Frühwirth-Schnatter and Kaufmann (2002)] develop a regime switching panel data model. Their purpose is to cluster many short time series to capture asymmetric effects of monetary policy on bank lending. [18] develop a finite mixture negative binomial count model to estimate six measures of medical care demand by the elderly. [11] offer a flexible Bayesian analysis of the problem of causal inference in models with non-randomly assigned treatments. Their approach is illustrated using hospice data and hip fracture data.