



Next: 5.3 Examples of the
Up: 5. The EM Algorithm
Previous: 5.1 Introduction
Subsections
5.2 Basic Theory of the EM Algorithm
5.2.1 The E- and M-Steps
Within the incomplete-data framework of the EM algorithm, we let
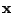 denote the vector containing the complete data and we let
denote the vector containing the complete data and we let
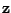 denote
the vector containing the
missing data. Even when a problem does not
at first appear to be an incomplete-data one, computation of the
MLE is often
greatly facilitated by artificially formulating it to be as such.
This is because the EM algorithm exploits the reduced complexity of
ML estimation given the complete data. For many statistical
problems the
complete-data likelihood has a nice form.
denote
the vector containing the
missing data. Even when a problem does not
at first appear to be an incomplete-data one, computation of the
MLE is often
greatly facilitated by artificially formulating it to be as such.
This is because the EM algorithm exploits the reduced complexity of
ML estimation given the complete data. For many statistical
problems the
complete-data likelihood has a nice form.
We let
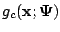 denote
the p.d.f. of the random vector
denote
the p.d.f. of the random vector
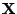 corresponding to the
complete-data vector
corresponding to the
complete-data vector
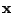 . Then the
complete-data log likelihood
function that could be formed for
. Then the
complete-data log likelihood
function that could be formed for
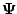 if
if
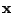 were fully observable
is given by
were fully observable
is given by
The EM algorithm approaches the problem of solving the
incomplete-data
likelihood (5.1) indirectly by proceeding iteratively
in terms of
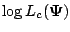 .
As it is unobservable, it is replaced by its conditional
expectation given
.
As it is unobservable, it is replaced by its conditional
expectation given
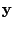 , using the current fit for
, using the current fit for
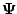 . On the
. On the
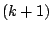 th iteration of the EM algorithm,
th iteration of the EM algorithm,
E-Step: Compute
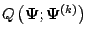 , where
, where
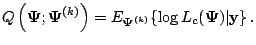 |
(5.2) |
M-Step: Choose
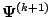 to be any value of
to be any value of
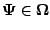 that maximizes
that maximizes
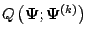 :
:
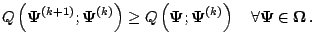 |
(5.3) |
In (5.2) and elsewhere in this chapter,
the operator
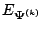 denotes expectation
using the parameter vector
denotes expectation
using the parameter vector
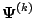 .
The
E- and M-steps are alternated repeatedly until
convergence, which
may be determined, for instance, by using a suitable
stopping rule like
.
The
E- and M-steps are alternated repeatedly until
convergence, which
may be determined, for instance, by using a suitable
stopping rule like
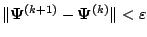 for some
for some
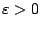 with some appropriate norm
with some appropriate norm
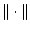 or the difference
or the difference
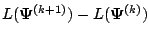 changes by an arbitrarily small
amount in the case of convergence of the sequence of likelihood values
changes by an arbitrarily small
amount in the case of convergence of the sequence of likelihood values
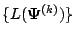 .
.
It can be shown that both the E- and M-steps
will have particularly simple forms when
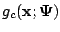 is from an
exponential family:
is from an
exponential family:
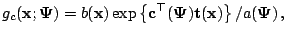 |
(5.4) |
where
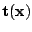 is a
is a
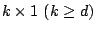 vector of
complete-data
sufficient statistics and
vector of
complete-data
sufficient statistics and
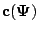 is a
is a
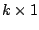 vector function of the
vector function of the
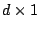 parameter vector
parameter vector
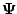 , and
, and
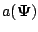 and
and
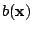 are scalar functions. Members
of the exponential family include most common distributions,
such as the multivariate normal, Poisson,
multinomial and others. For exponential
families, the
E-step can be written as
are scalar functions. Members
of the exponential family include most common distributions,
such as the multivariate normal, Poisson,
multinomial and others. For exponential
families, the
E-step can be written as
where
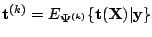 is an estimator of the sufficient statistic. The M-step maximizes
the
is an estimator of the sufficient statistic. The M-step maximizes
the 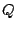 -function with respect to
-function with respect to
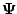 ; but
; but
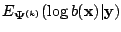 does not depend on
does not depend on
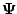 .
Hence it is sufficient to
write:
.
Hence it is sufficient to
write:
E-Step: Compute
M-Step: Compute
In Example 2 of Sect. 5.3.2, the complete-data p.d.f. has an
exponential family representation. We shall show how the implementation
of the EM algorithm can be simplified.
5.2.2 Generalized EM Algorithm
Often in practice, the solution to the M-step exists in closed form. In
those instances where it does not, it may not be feasible to attempt to
find the value of
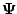 that globally maximizes the function
that globally maximizes the function
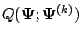 . For such situations, Dempster et al. (1977) defined a
generalized EM (GEM) algorithm for which the
M-Step requires
. For such situations, Dempster et al. (1977) defined a
generalized EM (GEM) algorithm for which the
M-Step requires
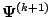 to be chosen such that
to be chosen such that
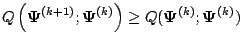 |
(5.5) |
holds. That is, one chooses
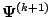 to increase the
to increase the
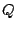 -function,
-function,
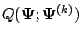 , over its value at
, over its value at
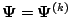 , rather
than to maximize it over all
, rather
than to maximize it over all
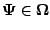 in (5.3).
in (5.3).
It is of interest to note that the EM (GEM) algorithm as described above
implicitly defines a mapping
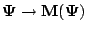 ,
from the parameter space
,
from the parameter space
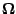 to itself such that
to itself such that
The function
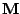 is called the
EM mapping. We shall use this function
in our subsequent discussion on the convergence property of the EM algorithm.
is called the
EM mapping. We shall use this function
in our subsequent discussion on the convergence property of the EM algorithm.
5.2.3 Convergence of the EM Algorithm
Let
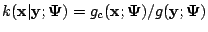 be the conditional density of
be the conditional density of
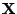 given
given
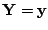 . Then the
complete-data log likelihood can be expressed by
. Then the
complete-data log likelihood can be expressed by
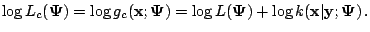 |
(5.6) |
Taking expectations on both sides of (5.6) with respect
to the conditional distribution
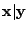 using the fit
using the fit
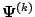 for
for
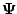 , we have
, we have
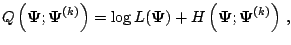 |
(5.7) |
where
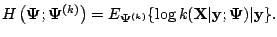 It follows from (5.7) that
It follows from (5.7) that
By Jensen's inequality, we have
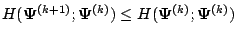 . From (5.3) or (5.5),
the first difference on the right-hand side
of (5.8) is nonnegative. Hence, the likelihood function
is not decreased after an EM or
GEM iteration:
. From (5.3) or (5.5),
the first difference on the right-hand side
of (5.8) is nonnegative. Hence, the likelihood function
is not decreased after an EM or
GEM iteration:
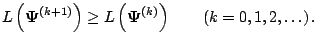 |
(5.9) |
A consequence of (5.9) is the
self-consistency of the EM
algorithm.
Thus for a bounded sequence of likelihood values
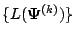 ,
,
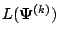 converges monotonically to some
converges monotonically to some 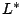 .
Now questions naturally arise as to the conditions under which
.
Now questions naturally arise as to the conditions under which
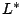 corresponds to a stationary value and when this stationary
value is at least a
local maximum if not a global maximum. Examples are
known where the EM algorithm converges to
a local minimum and to a saddle point of the
likelihood (McLachlan and Krishnan, 1997, Sect. 3.6).
There are also questions of convergence of the sequence of EM
iterates, that is, of the sequence of parameter values
corresponds to a stationary value and when this stationary
value is at least a
local maximum if not a global maximum. Examples are
known where the EM algorithm converges to
a local minimum and to a saddle point of the
likelihood (McLachlan and Krishnan, 1997, Sect. 3.6).
There are also questions of convergence of the sequence of EM
iterates, that is, of the sequence of parameter values
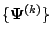 to the MLE.
to the MLE.
Before the general formulation of the EM algorithm in
Dempster et al. (1977), there have been convergence results for special
cases, notable among them being those of Baum et al. (1970) for
what is now being called the
hidden Markov model. In the article
of Dempster et al. (1977) itself, there are some convergence
results. However, it is Wu (1983) who investigates in detail
several convergence issues of the EM algorithm in its
generality. Wu examines these issues through their relationship
to other optimization methods. He shows that when the complete
data are from a curved exponential family with compact parameter
space, and when the 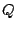 -function satisfies a certain mild differentiability
condition, then any EM sequence converges to a stationary point
(not necessarily a maximum) of the likelihood function. If
-function satisfies a certain mild differentiability
condition, then any EM sequence converges to a stationary point
(not necessarily a maximum) of the likelihood function. If
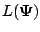 has multiple stationary points, convergence of the
EM sequence to either type (local or global maximizers, saddle
points) depends upon the
starting value
has multiple stationary points, convergence of the
EM sequence to either type (local or global maximizers, saddle
points) depends upon the
starting value
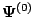 for
for
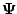 .
If
.
If
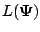 is unimodal in
is unimodal in
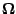 and satisfies the same
differentiability condition, then any sequence
and satisfies the same
differentiability condition, then any sequence
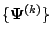 will converge to the unique MLE of
will converge to the unique MLE of
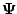 , irrespective of its
starting value.
, irrespective of its
starting value.
To be more specific, one of the basic
convergence results of the
EM algorithm is the following:
with equality if and only if
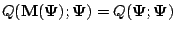 and and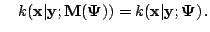 |
|
This means that the likelihood function increases at each iteration of
the EM algorithm, until the condition for equality is satisfied and
a fixed point of the iteration is reached. If
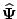 is an MLE, so that
is an MLE, so that
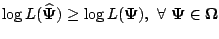 , then
, then
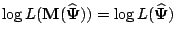 . Thus MLE are fixed points of the EM
algorithm. If we have the likelihood function bounded (as might
happen in many cases of interest), the EM sequence
. Thus MLE are fixed points of the EM
algorithm. If we have the likelihood function bounded (as might
happen in many cases of interest), the EM sequence
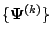 yields a bounded nondecreasing sequence
yields a bounded nondecreasing sequence
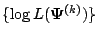 which must converge as
which must converge as
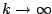 .
.
The theorem does not quite imply that fixed points of the EM algorithm
are in fact MLEs. This is however true under fairly general
conditions. For proofs and other details, see McLachlan and Krishnan
(1997, Sect. 3.5) and Wu (1983). Furthermore, if a sequence of EM
iterates
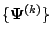 satisfy the conditions
satisfy the conditions
-
![$ [\partial Q(\mathbf{\Psi}; \mathbf{\Psi}^{(k)}) /
\partial \mathbf{\Psi}]_{\mathbf{\Psi}=\mathbf{\Psi}^{(k+1)}} = \boldsymbol{0}$](img1878.gif) , and
, and
- the sequence
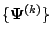 converges to some value
converges to some value
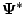 and
and
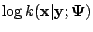 is sufficiently
smooth,
is sufficiently
smooth,
then we have
![$ [\partial \log L(\mathbf{\Psi}) /
\partial \mathbf{\Psi}]_{\mathbf{\Psi}=\mathbf{\Psi}^{\ast}} = \boldsymbol{0}$](img1880.gif) ; see Little and
Rubin (2002) and Wu (1983). Thus, despite the
earlier convergence results, there is no guarantee that the
convergence will be to a global maximum. For likelihood
functions with multiple maxima, convergence will be to a local
maximum which depends on the starting value
; see Little and
Rubin (2002) and Wu (1983). Thus, despite the
earlier convergence results, there is no guarantee that the
convergence will be to a global maximum. For likelihood
functions with multiple maxima, convergence will be to a local
maximum which depends on the starting value
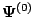 .
.
Nettleton (1999) extends Wu's convergence results
to the case of constrained parameter spaces and establishes some
stricter conditions to guarantee convergence of the EM likelihood
sequence to some local maximum and the EM parameter iterates to
converge to the MLE.
5.2.4 Rate of Convergence of the EM Algorithm
The rate of convergence of the EM algorithm is also of practical
interest. The convergence rate is usually slower than the
quadratic convergence typically available with Newton-type
methods. Dempster et al. (1977)
show that the rate of convergence of the EM algorithm
is linear and the rate depends on the proportion of information
in the observed data. Thus
in comparison to the formulated complete-data problem, if a large
portion of data is missing, convergence can be quite slow.
Recall the EM mapping
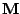 defined in Sect. 5.2.2. If
defined in Sect. 5.2.2. If
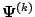 converges to some point
converges to some point
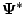 and
and
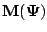 is continuous, then
is continuous, then
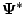 is a fixed point of
the algorithm; that is,
is a fixed point of
the algorithm; that is,
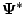 must satisfy
must satisfy
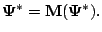 By a Taylor series expansion of
By a Taylor series expansion of
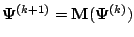 about the point
about the point
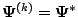 , we have in
a neighborhood of
, we have in
a neighborhood of
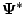 that
that
where
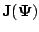 is the
is the
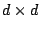 Jacobian matrix for
Jacobian matrix for
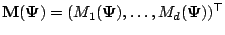 , having
, having 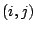 th
element
th
element
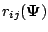 equal to
equal to
where
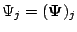 and
and 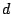 is the dimension of
is the dimension of
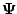 .
Thus, in a neighborhood of
.
Thus, in a neighborhood of
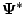 , the EM algorithm is
essentially a linear iteration with rate matrix
, the EM algorithm is
essentially a linear iteration with rate matrix
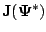 , since
, since
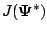 is typically nonzero.
For this reason,
is typically nonzero.
For this reason,
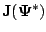 is often referred to as the
matrix rate of convergence. For vector
is often referred to as the
matrix rate of convergence. For vector
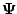 , a measure of the
actual observed convergence rate is the global rate of convergence,
which is defined as
, a measure of the
actual observed convergence rate is the global rate of convergence,
which is defined as
where
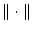 is any norm on
is any norm on 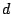 -dimensional
Euclidean space
-dimensional
Euclidean space 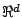 . It is noted that the observed rate of
convergence equals the largest eigenvalue of
. It is noted that the observed rate of
convergence equals the largest eigenvalue of
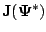 under certain regularity conditions
(Meng and van Dyk, 1997). As a large value of
under certain regularity conditions
(Meng and van Dyk, 1997). As a large value of 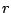 implies slow
convergence, the global speed of convergence is defined to be
implies slow
convergence, the global speed of convergence is defined to be 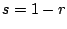 (Meng, 1994).
(Meng, 1994).
The EM algorithm has several appealing
properties, some of which are:
- It is numerically stable with each EM
iteration increasing the likelihood.
- Under fairly general conditions, it has
reliable global convergence.
- It is easily implemented, analytically
and computationally. In particular, it is generally easy to program
and requires small storage space.
By watching the monotone increase in likelihood (if evaluated
easily) over iterations, it is easy to monitor convergence and
programming errors (McLachlan and Krishnan, 1997, Sect. 1.7).
- The cost per iteration is generally low, which can offset the
larger number of iterations needed for the EM algorithm compared to
other competing procedures.
- It can be used to provide estimates of
missing data.
Some of its drawbacks are:
- It does not automatically provide an estimate of the
covariance matrix of the parameter estimates.
However, this disadvantage can be
easily removed by using appropriate methodology associated with the
EM algorithm (McLachlan and Krishnan, 1997, Chap. 4).
- It is sometimes very slow to converge.
- In some problems, the E- or M-steps may be
analytically intractable.
We shall briefly address these three issues in Sects. 5.3.5 and 5.4.




Next: 5.3 Examples of the
Up: 5. The EM Algorithm
Previous: 5.1 Introduction
![]() denote the vector containing the complete data and we let
denote the vector containing the complete data and we let
![]() denote
the vector containing the
missing data. Even when a problem does not
at first appear to be an incomplete-data one, computation of the
MLE is often
greatly facilitated by artificially formulating it to be as such.
This is because the EM algorithm exploits the reduced complexity of
ML estimation given the complete data. For many statistical
problems the
complete-data likelihood has a nice form.
denote
the vector containing the
missing data. Even when a problem does not
at first appear to be an incomplete-data one, computation of the
MLE is often
greatly facilitated by artificially formulating it to be as such.
This is because the EM algorithm exploits the reduced complexity of
ML estimation given the complete data. For many statistical
problems the
complete-data likelihood has a nice form.
![]() denote
the p.d.f. of the random vector
denote
the p.d.f. of the random vector
![]() corresponding to the
complete-data vector
corresponding to the
complete-data vector
![]() . Then the
complete-data log likelihood
function that could be formed for
. Then the
complete-data log likelihood
function that could be formed for
![]() if
if
![]() were fully observable
is given by
were fully observable
is given by
![]() , where
, where
![]() to be any value of
to be any value of
![]() that maximizes
that maximizes
![]() :
:
![]() is from an
exponential family:
is from an
exponential family:
![]() ,
from the parameter space
,
from the parameter space
![]() to itself such that
to itself such that
![]() -function satisfies a certain mild differentiability
condition, then any EM sequence converges to a stationary point
(not necessarily a maximum) of the likelihood function. If
-function satisfies a certain mild differentiability
condition, then any EM sequence converges to a stationary point
(not necessarily a maximum) of the likelihood function. If
![]() has multiple stationary points, convergence of the
EM sequence to either type (local or global maximizers, saddle
points) depends upon the
starting value
has multiple stationary points, convergence of the
EM sequence to either type (local or global maximizers, saddle
points) depends upon the
starting value
![]() for
for
![]() .
If
.
If
![]() is unimodal in
is unimodal in
![]() and satisfies the same
differentiability condition, then any sequence
and satisfies the same
differentiability condition, then any sequence
![]() will converge to the unique MLE of
will converge to the unique MLE of
![]() , irrespective of its
starting value.
, irrespective of its
starting value.
![]() satisfy the conditions
satisfy the conditions
![]() defined in Sect. 5.2.2. If
defined in Sect. 5.2.2. If
![]() converges to some point
converges to some point
![]() and
and
![]() is continuous, then
is continuous, then
![]() is a fixed point of
the algorithm; that is,
is a fixed point of
the algorithm; that is,
![]() must satisfy
must satisfy
![]() By a Taylor series expansion of
By a Taylor series expansion of
![]() about the point
about the point
![]() , we have in
a neighborhood of
, we have in
a neighborhood of
![]() that
that