next up previous contents index
Next: 5.5 Miscellaneous Topics on Up: 5. The EM Algorithm Previous: 5.3 Examples of the

Subsections


5.4 Variations on the EM Algorithm

In this section, further modifications and extensions to the EM algorithm are considered. In general, there are extensions of the EM algorithm

  1. to produce standard errors of the MLE using the EM;
  2. to surmount problems of difficult E-step and/or M-step computations;
  3. to tackle problems of slow convergence;
  4. in the direction of Bayesian or regularized or penalized ML estimations.
We have already discussed methods like the SEM algorithm for producing standard errors of EM-computed MLE in Sect. 5.3.5. The modification of the EM algorithm for Bayesian inference will be discussed in Sect. 5.5.1. In this section, we shall focus on the problems of complicated E- or M-steps and of slow convergence of the EM algorithm.


5.4.1 Complicated E-Step

In some applications of the EM algorithm, the E-step is complex and does not admit a close-form solution to the $ Q$-function. In this case, the E-step at the $ (k+1)$th iteration may be executed by a Monte Carlo (MC) process:

  1. Make $ M$ independent draws of the missing values $ \boldsymbol{Z}$, $ \boldsymbol{z}^{(1_k)},\ldots,\boldsymbol{z}^{(M_k)}$, from the conditional distribution $ k(\boldsymbol{z}\vert\boldsymbol{y}; \boldsymbol{\Psi}^{(k)})$.
  2. Approximate the $ Q$-function as

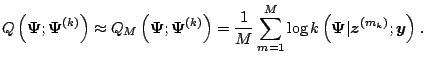    $\displaystyle \notag Q\left(\boldsymbol{\Psi}; \boldsymbol{\Psi}^{(k)}\right) \... ...g k\left(\boldsymbol{\Psi}\vert\boldsymbol{z}^{(m_k)}; \boldsymbol{y}\right)\,.$    

In the M-step, the $ Q$-function is maximized over $ \boldsymbol{\Psi}$ to obtain $ \boldsymbol{\Psi}^{(k+1)}$. The variant is known as the Monte Carlo EM (MCEM) algorithm (Wei and Tanner, 1990). As MC error is introduced at the E-step, the monotonicity property is lost. But in certain cases, the algorithm gets close to a maximizer with a high probability (Booth and Hobert, 1999). The problems of specifying $ M$ and monitoring convergence are of central importance in the routine use of the algorithm. Wei and Tanner (1990) recommend small values of $ M$ be used in initial stages and be increased as the algorithm moves closer to convergence. As to monitoring convergence, they recommend that the values of $ \boldsymbol{\Psi}^{(k)}$ be plotted against $ k$ and when convergence is indicated by the stabilization of the process with random fluctuations about $ \widehat{\boldsymbol{\Psi}}$, the process may be terminated or continued with a larger value of $ M$. Alternative schemes for specifying $ M$ and stopping rule are considered by Booth and Hobert (1999) and McCulloch (1997).


5.4.1.1 Example 4: Generalized Linear Mixed Models

Generalized linear mixed models (GLMM) are extensions of generalized linear models (GLM) (McCullagh and Nelder, 1989) that incorporate random effects in the linear predictor of the GLM (more material on the GLM can be found in Chap. III.7). We let $ \boldsymbol{y}=(y_1,\ldots,y_n)^{\top}$ denote the observed data vector. Conditional on the unobservable random effects vector, $ \boldsymbol{u}=(u_1,\ldots,u_q)^{\top}$, we assume that $ \boldsymbol {y}$ arise from a GLM. The conditional mean $ \mu_j=E(y_j\vert\boldsymbol{u})$ is related to the linear predictor $ \eta_j=\boldsymbol{x}_j^{\top} \boldsymbol{\beta} + \boldsymbol{z}_j^{\top} \boldsymbol{u}$ by the link function $ g(\mu_j)=\eta_j \ (j=1,\ldots,n)$, where $ \boldsymbol {\beta }$ is a $ p$-vector of fixed effects and $ \boldsymbol{x}_j$ and $ \boldsymbol{z}_j$ are, respectively, $ p$-vector and $ q$-vector of explanatory variables associated with the fixed and random effects. This formulation encompasses the modeling of data involving multiple sources of random error, such as repeated measures within subjects and clustered data collected from some experimental units (Breslow and Clayton, 1993).

We let the distribution for $ \boldsymbol {u}$ be $ g(\boldsymbol{u};\boldsymbol{D})$ that depends on parameters $ \boldsymbol{D}$. The observed data $ \boldsymbol {y}$ are conditionally independent with density functions of the form

$\displaystyle f(y_j\vert\boldsymbol{u}; \boldsymbol{\beta},\kappa)= \exp \left[ m_j \kappa^{-1} \{ \theta_j y_j - b(\theta_j) \} + c(y_j; \kappa) \right]\,,$ (5.23)

where $ \theta_j$ is the canonical parameter, $ \kappa$ is the dispersion parameter, and $ m_j$ is the known prior weight. The conditional mean and canonical parameters are related through the equation $ \mu_j=b'(\theta_j)$, where the prime denotes differentiation with respect to $ \theta_j$. Let $ \boldsymbol{\Psi}$ denotes the vector of unknown parameters within $ \boldsymbol {\beta }$, $ \kappa$, and $ \boldsymbol{D}$. The likelihood function for $ \boldsymbol{\Psi}$ is given by

$\displaystyle L(\boldsymbol{\Psi}) = \int \prod_{j=1}^{n} f(y_j\vert\boldsymbol... ...ol{\beta},\kappa) g(\boldsymbol{u};\boldsymbol{D}) {\text{d}} \boldsymbol{u}\,,$ (5.24)

which cannot usually be evaluated in closed form and has an intractable integral whose dimension depends on the structure of the random effects.

Within the EM framework, the random effects are considered as missing data. The complete data is then $ \boldsymbol{x}=(\boldsymbol{y}^{\top},\boldsymbol{u}^{\top})^{\top}$ and the complete-data log likelihood is given by

$\displaystyle \log L_c(\boldsymbol{\Psi}) = \sum_{j=1}^{n} \log f(y_j\vert\boldsymbol{u}; \boldsymbol{\beta},\kappa) + \log g(\boldsymbol{u};\boldsymbol{D})\,.$ (5.25)

On the $ (k+1)$th iteration of the EM algorithm, the E-step involves the computation of the $ Q$-function, $ Q(\boldsymbol{\Psi}; \boldsymbol{\Psi}^{(k)}) = E_{\boldsymbol{\Psi}^{(k)}} \{ \log L_c(\boldsymbol{\Psi}) \vert \boldsymbol{y} \}$, where the expectation is with respect to the conditional distribution of $ \boldsymbol{u}\vert\boldsymbol{y}$ with current parameter value $ \boldsymbol{\Psi}^{(k)}$. As this conditional distribution involves the (marginal) likelihood function $ L(\boldsymbol{\Psi})$ given in (5.24), an analytical evaluation of the $ Q$-function for the model (5.23) will be impossible outside the normal theory mixed model (Booth and Hobert, 1999). The MCEM algorithm can be adopted to tackle this problem by replacing the expectation in the E-step with a MC approximation. Let $ \boldsymbol{u}^{(1_k)},\ldots,\boldsymbol{u}^{(M_k)}$ denote a random sample from $ k(\boldsymbol{u}\vert\boldsymbol{y}; \boldsymbol{\Psi}^{(k)})$ at the $ (k+1)$th iteration. A MC approximation of the $ Q$-function is given by

$\displaystyle Q_M\left(\boldsymbol{\Psi}; \boldsymbol{\Psi}^{(k)}\right) = \fra... ...a\right) + \log g\left(\boldsymbol{u}^{(m_k)};\boldsymbol{D}\right) \right\}\,.$ (5.26)

From (5.26), it can be seen that the first term of the approximated $ Q$-function involves only parameters $ \boldsymbol {\beta }$ and $ \kappa$, while the second term involves only $ \boldsymbol{D}$. Thus, the maximization in the MC M-step is usually relatively simple within the GLMM context (McCulloch, 1997).

Alternative simulation schemes for $ \boldsymbol {u}$ can be used for (5.26). For example, Booth and Hobert (1999) proposed the rejection sampling and a multivariate $ t$ importance sampling approximations. McCulloch (1997) considered dependent MC samples using MC Newton-Raphson (MCNR) algorithm.

5.4.2 Complicated M-Step

One of major reasons for the popularity of the EM algorithm is that the M-step involves only complete-data ML estimation, which is often computationally simple. But if the complete-data ML estimation is rather complicated, then the EM algorithm is less attractive. In many cases, however, complete-data ML estimation is relatively simple if maximization process on the M-step is undertaken conditional on some functions of the parameters under estimation. To this end, Meng and Rubin (1993) introduce a class of GEM algorithms, which they call the Expectation-Conditional Maximization (ECM) algorithm.


5.4.2.1 ECM and Multicycle ECM Algorithms

The ECM algorithm takes advantage of the simplicity of complete-data conditional maximization by replacing a complicated M-step of the EM algorithm with several computationally simpler conditional maximization (CM) steps. Each of these CM-steps maximizes the $ Q$-function found in the preceding E-step subject to constraints on $ \boldsymbol{\Psi}$, where the collection of all constraints is such that the maximization is over the full parameter space of $ \boldsymbol{\Psi}$.

A CM-step might be in closed form or it might itself require iteration, but because the CM maximizations are over smaller dimensional spaces, often they are simpler, faster, and more stable than the corresponding full maximizations called for on the M-step of the EM algorithm, especially when iteration is required. The ECM algorithm typically converges more slowly than the EM in terms of number of iterations, but can be faster in total computer time. More importantly, the ECM algorithm preserves the appealing convergence properties of the EM algorithm, such as its monotone convergence.

We suppose that the M-step is replaced by $ S > 1$ steps and let $ \boldsymbol{\Psi}^{(k+s/S)}$ denote the value of $ \boldsymbol{\Psi}$ on the $ s$th CM-step of the $ (k+1)$th iteration. In many applications of the ECM algorithm, the $ S$ CM-steps correspond to the situation where the parameter vector $ \boldsymbol{\Psi}$ is partitioned into $ S$ subvectors,

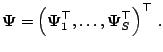$\displaystyle \notag \boldsymbol{\Psi}=\left(\boldsymbol{\Psi}_1^{\top}, \ldots, \boldsymbol{\Psi}_S^{\top}\right)^{\top}\,.$    

The $ s$th CM-step then requires the maximization of the $ Q$-function with respect to the $ s$th subvector $ \boldsymbol{\Psi}_s$ with the other $ (S-1)$ subvectors held fixed at their current values. The convergence properties and the rate of convergence of the ECM algorithm have been discussed in Meng (1994) and Meng and Rubin (1993); see also the discussion in Sexton and Swensen (2000). In particular, it can be shown that

$\displaystyle Q\left(\boldsymbol{\Psi}^{(k+1)}; \boldsymbol{\Psi}^{(k)}\right)\... ...q \ldots \geq Q\left(\boldsymbol{\Psi}^{(k)}; \boldsymbol{\Psi}^{(k)}\right)\,.$ (5.27)

This shows that the ECM algorithm is a GEM algorithm and so possesses its desirable convergence properties. As noted in Sect. 5.2.3, the inequality (5.27) is a sufficient condition for

$\displaystyle L\left(\boldsymbol{\Psi}^{(k+1)}\right)\geq L\left(\boldsymbol{\Psi}^{(k)}\right)$ (5.28)

to hold.

In many cases, the computation of an E-step may be much cheaper than the computation of the CM-steps. Hence one might wish to perform one E-step before each CM-step. A cycle is defined to be one E-step followed by one CM-step. The corresponding algorithm is called the multicycle ECM (Meng and Rubin, 1993). A multicycle ECM may not necessarily be a GEM algorithm; that is, the inequality (5.27) may not be hold. However, it is not difficult to show that the multicycle ECM algorithm monotonically increases the likelihood function $ L(\boldsymbol{\Psi})$ after each cycle, and hence, after each iteration. The convergence results of the ECM algorithm apply to a multicycle version of it. An obvious disadvantage of using a multicycle ECM algorithm is the extra computation at each iteration. Intuitively, as a tradeoff, one might expect it to result in larger increases in the log likelihood function per iteration since the $ Q$-function is being updated more often (Meng, 1994; Meng and Rubin, 1993).


5.4.2.2 Example 5: Single-Factor Analysis Model

Factor analysis is commonly used for explaining data, in particular, correlations between variables in multivariate observations and for dimensionality reduction. In a typical factor analysis model, each observation $ \boldsymbol{Y}_j$ is modeled as

$\displaystyle \boldsymbol{Y}_j = \boldsymbol{\mu} + \boldsymbol{B}\boldsymbol{U}_j + \boldsymbol{e}_j \quad(j=1, \ldots, n)\,,$ (5.29)

where $ \boldsymbol{U}_j$ is a $ q$-dimensional ($ q < p$) vector of latent or unobservable variables called factors and $ \boldsymbol{B}$ is a $ p \times q$ matrix of factor loadings (parameters). The $ \boldsymbol{U}_j$ are assumed to be i.i.d. as $ N({\boldsymbol{O}}, {\boldsymbol{I}}_q)$, independently of the errors $ \boldsymbol{e}_j$, which are assumed to be i.i.d. as $ N(\boldsymbol{O}, \boldsymbol{D})$, where $ \boldsymbol{D} =$   diag$ (\sigma_1^2, \ldots, \sigma_p^2)$, and where $ \boldsymbol{I}_q$ denotes the $ q \times q$ identity matrix. Thus, conditional on $ \boldsymbol{U}_j=\boldsymbol{u}_j$, the $ Y_j$ are independently distributed as $ N(\boldsymbol{\mu} +\boldsymbol{B} \boldsymbol{u}_j, \boldsymbol{D})$. Unconditionally, the $ \boldsymbol{Y}_j$ are i.i.d. according to a normal distribution with mean $ \boldsymbol{\mu}$ and covariance matrix

$\displaystyle \boldsymbol{\Sigma}=\boldsymbol{B}\boldsymbol{B}^{\top} + \boldsymbol{D}\,.$ (5.30)

If $ q$ is chosen sufficiently smaller than $ p$, representation (5.30) imposes some constraints on $ \boldsymbol{\Sigma}$ and thus reduces the number of free parameters to be estimated. Note that in the case of $ q>1$, there is an infinity of choices for $ \boldsymbol{B}$, since (5.30) is still satisfied if $ \boldsymbol{B}$ is replaced by $ \boldsymbol{B} \boldsymbol{C}$, where $ \boldsymbol{C}$ is any orthogonal matrix of order $ q$. As $ {\textstyle\frac{1}{2}}q(q-1)$ constraints are needed for $ \boldsymbol{B}$ to be uniquely defined, the number of free parameters is $ pq + p- {\textstyle\frac{1}{2}}q(q-1);$ see Lawley and Maxwell (1971, Chap. 1) and McLachlan et al. (2003).

The factor analysis model (5.29) can be fitted by the EM algorithm and its variants. The MLE of the mean $ \boldsymbol{\mu}$ is obviously the sample mean $ \boldsymbol{\mu}$ of the $ n$ observed values $ \boldsymbol{y}_1, \ldots, \boldsymbol{y}_n$ corresponding to the random sample $ \boldsymbol{Y}_1, \ldots, \boldsymbol{Y}_n$. Hence in the sequel, $ \boldsymbol{\mu}$ can be set equal to $ \boldsymbol{\mu}$ without loss of generality. The log likelihood for $ \boldsymbol{\Psi}$ that can be formed from the observed data $ \boldsymbol{y}=(\boldsymbol{y}_1^{\top}, \ldots, \boldsymbol{y}_n^{\top})^{\top}$ is, apart from an additive constant,

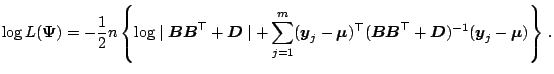$\displaystyle \notag \log L(\boldsymbol{\Psi}) = -{\frac{1}{2}}n\left\{\log\mid... ...l{B}^{\top}+\boldsymbol{D})^{-1} (\boldsymbol{y}_j-\boldsymbol{\mu})\right\}\,.$    

We follow Dempster et al. (1977) and formulate $ \boldsymbol{x} = (\boldsymbol{y}^{\top}, \boldsymbol{u}_1^{\top}, \ldots, \boldsymbol{u}_n^{\top})^{\top}$ as the complete-data vector, where $ \boldsymbol{u}_j$ corresponds to $ \boldsymbol{U}_j$. Thus, the complete-data log likelihood is, but for an additive constant,

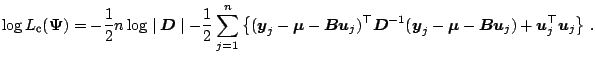$\displaystyle \notag \log L_{{\text{c}}}(\boldsymbol{\Psi}) = -{\frac{1}{2}}n\l... ...symbol{B}\boldsymbol{u}_j) + \boldsymbol{u}_j^{\top}\boldsymbol{u}_j\right\}\,.$    

The complete-data density belongs to the exponential family, and the complete-data sufficient statistics are $ \boldsymbol{C}_{yy}, \boldsymbol{C}_{yu},$ and $ \boldsymbol{C}_{uu}$, where

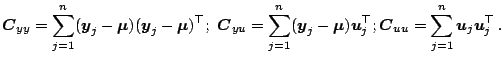$\displaystyle \notag \boldsymbol{C}_{yy} = \sum_{j=1}^n (\boldsymbol{y}_j-\bold... ...}; \boldsymbol{C}_{uu} =\sum_{j=1}^n \boldsymbol{u}_j\boldsymbol{u}_j^{\top}\,.$    

On the $ (k+1)$th iteration of the EM algorithm, we have

E-Step: Compute the conditional expectation of the sufficient statistics given $ \boldsymbol {y}$ and the current fit $ \boldsymbol{\Psi}^{(k)}$ for $ \boldsymbol{\Psi}$:

$\displaystyle \notag E_{\boldsymbol{\Psi}^{(k)}}(\boldsymbol{C}_{yy} \mid \bold... ...{C}_{yu} \mid \boldsymbol{y}) = \boldsymbol{C}_{yy}\boldsymbol{\gamma}^{(k)}\,,$    

and

$\displaystyle \notag E_{\boldsymbol{\Psi}^{(k)}}(\boldsymbol{C}_{uu} \mid \bold... ...} \boldsymbol{C}_{yy} \boldsymbol{\gamma}^{(k)} + n\boldsymbol{\omega}^{(k)}\,,$    

where

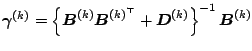$\displaystyle \notag \boldsymbol{\gamma}^{(k)} = \left\{\boldsymbol{B}^{(k)}\boldsymbol{B}^{(k)^{\top}}+\boldsymbol{D}^{(k)}\right\}^{-1}\boldsymbol{B}^{(k)}$   and$\displaystyle \quad \boldsymbol{\omega}^{(k)} =\boldsymbol{I}_q-\boldsymbol{\gamma}^{(k)^{\top}}\boldsymbol{B}^{(k)}\,.$    

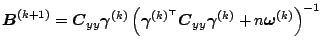M-Step: Calculate $ \boldsymbol{B}^{(k+1)} =\boldsymbol{C}_{yy} \boldsymbol{\gamma}^{(k)} \left(\b... ...mbol{C}_{yy} \boldsymbol{\gamma}^{(k)} + n\boldsymbol{\omega}^{(k)}\right)^{-1}$ and

$\displaystyle \boldsymbol{D}^{(k+1)}$ $\displaystyle = {{\text{diag}}} \left\{\boldsymbol{C}_{yy}/n - \boldsymbol{B}^{(k+1)} \boldsymbol{H}^{(k)} \boldsymbol{B}^{(k+1)^{\top}}\right\}$    
  $\displaystyle = n^{-1} \,{{\text{diag}}}\left\{\boldsymbol{C}_{yy} -\boldsymbol{C}_{yy}\boldsymbol{\gamma}^{(k)}\boldsymbol{B}^{(k+1)^{\top}}\right\}\,,$ (5.31)

where

$\displaystyle \boldsymbol{H}^{(k)} = E_{\boldsymbol{\Psi}^{(k)}}(\boldsymbol{C}... ... \boldsymbol{C}_{yy} \boldsymbol{\gamma}^{(k)}/n + \boldsymbol{\omega}^{(k)}\,.$ (5.32)

It is noted that direct differentiation of $ \log L(\boldsymbol{\Psi})$ shows that the ML estimate of the diagonal matrix $ \boldsymbol{D}$ satisfies

$\displaystyle \widehat{\boldsymbol{D}}={{\text{diag}}} \left\{ \boldsymbol{C}_{yy}/n -\widehat{\boldsymbol{B}} \widehat{\boldsymbol{B}}^{\top} \right\}\, .$ (5.33)

As remarked by Lawley and Maxwell (1971, pp. 30), (5.33) looks temptingly simple to use to solve for $ \widehat{\boldsymbol{D}}$, but was not recommended due to convergence problems. On comparing (5.33) with (5.31), it can be seen that with the calculation of the ML estimate of $ \boldsymbol{D}$ directly from $ \log L(\boldsymbol{\Psi})$, the unconditional expectation of $ \boldsymbol{U}_j \boldsymbol{U}_j^{\top}$, which is the identity matrix, is used in place of the conditional expectation in (5.32) on the E-step. Although the EM algorithm is numerically stable, the rate of convergence is slow, which can be attributed to the typically large fraction of missing data. Liu and Rubin (1994, 1998) have considered the application of the ECME algorithm to this problem; see Sect. 5.4.3 for the description of the algorithm. The M-step is replaced by two CM-steps. On the first CM-step, $ \boldsymbol{B}^{(k+1)}$ is calculated as on the M-step above, while on the second CM-step the diagonal matrix $ \boldsymbol{D}^{(k+1)}$ is obtained by using an algorithm such as Newton-Raphson to maximize the actual log likelihood with $ \boldsymbol{B}$ fixed at $ \boldsymbol{B}^{(k+1)}$.

The single-factor analysis model provides only a global linear model for the representation of the data in a lower-dimensional subspace, the scope of its application is limited. A global nonlinear approach can be obtained by postulating a mixture of linear submodels for the distribution of the full observation vector $ \boldsymbol{Y}_j$ given the (unobservable) factors $ \boldsymbol{u}_j$ (McLachlan et al., 2003). This mixture of factor analyzers has been adopted both (a) for model-based density estimation from high-dimensional data, and hence for the clutering of such data, and (b) for local dimensionality reduction; see for example McLachlan and Peel (2000, Chap. 8). Some more material on dimension reduction methods can be found in Chap. III.6 of this handbook.


5.4.3 Speeding up Convergence

Several suggestions are available in the literature for speeding up convergence, some of a general kind and some problem-specific; see for example McLachlan and Krishnan (1997, Chap. 4). Most of them are based on standard numerical analytic methods and suggest a hybrid of EM with methods based on Aitken acceleration, over-relaxation, line searches, Newton methods, conjugate gradients, etc. Unfortunately, the general behaviour of these hybrids is not always clear and they may not yield monotonic increases in the log likelihood over iterations. There are also methods that approach the problem of speeding up convergence in terms of ''efficient'' data augmentation scheme (Meng and van Dyk, 1997). Since the convergence rate of the EM algorithm increases with the proportion of observed information in the prescribed EM framework (Sect. 5.2.4), the basic idea of the scheme is to search for an efficient way of augmenting the observed data. By efficient, they mean less augmentation of the observed data (greater speed of convergence) while maintaining the simplicity and stability of the EM algorithm. A common trade-off is that the resulting E- and/or M-steps may be made appreciably more difficult to implement. To this end, Meng and van Dyk (1997) introduce a working parameter in their specification of the complete data to index a class of possible schemes to facilitate the search.


5.4.3.1 ECME, AECM, and PX-EM Algorithms

Liu and Rubin (1994, 1998) present an extension of the ECM algorithm called the ECME (expectation-conditional maximization either) algorithm. Here the ''either'' refers to the fact that with this extension, each CM-step either maximizes the $ Q$-function or the actual (incomplete-data) log likelihood function $ \log L(\boldsymbol{\Psi})$, subject to the same constraints on $ \boldsymbol{\Psi}$. The latter choice should lead to faster convergence as no augmentation is involved. Typically, the ECME algorithm is more tedious to code than the ECM algorithm, but the reward of faster convergence is often worthwhile especially because it allows convergence to be more easily assessed.

A further extension of the EM algorithm, called the Space-Alternating Generalized EM (SAGE), has been proposed by Fessler and Hero (1994), where they update sequentially small subsets of parameters using appropriately smaller complete data spaces. This approach is eminently suitable for situations like image reconstruction where the parameters are large in number. Meng and van Dyk (1997) combined the ECME and SAGE algorithms. The so-called Alternating ECM (AECM) algorithm allows the data augmentation scheme to vary where necessary over the CM-steps, within and between iterations. With this flexible data augmentation and model reduction schemes, the amount of data augmentation decreases and hence efficient computations are achieved.

In contrast to the AECM algorithm where the optimal value of the working parameter is determined before EM iterations, a variant is considered by Liu et al. (1998) which maximizes the complete-data log likelihood as a function of the working parameter within each EM iteration. The so-called parameter-expanded EM (PX-EM) algorithm has been used for fast stable computation of MLE in a wide range of models. This variant has been further developed, known as the one-step-late PX-EM algorithm, to compute MAP or maximum penalized likelihood (MPL) estimates (van Dyk and Tang, 2003). Analogous convergence results hold for the ECME, AECM, and PX-EM algorithms as for the EM and ECM algorithms. More importantly, these algorithms preserve the monotone convergence of the EM algorithm as stated in (5.28).


5.4.3.2 Extensions to the EM for Data Mining Applications

With the computer revolution, massively huge data sets of millions of multidimensional observations are now commonplace. There is an ever increasing demand on speeding up the convergence of the EM algorithm to large databases. But at the same time, it is highly desirable if its simplicity and stability can be preserved. In applications where the M-step is computationally simple, for example, in fitting mutivariate normal mixtures, the rate of convergence of the EM algorithm depends mainly on the computation time of an E-step as each data point is visited at each E-step. There have been some promising developments on modifications to the EM algorithm for the ML fitting of mixture models to large databases that preserve the simplicity of implementation of the EM in its standard form.

Neal and Hinton (1998) proposed the incremental EM (IEM) algorithm to improve the convergence rate of the EM algorithm. With this algorithm, the available $ n$ observations are divided into $ B \ (B \leq n)$ blocks and the E-step is implemented for only a block of data at a time before performing a M-step. A ''scan'' of the IEM algorithm thus consists of $ B$ partial E-steps and $ B$ M-steps. The argument for improved rate of convergence is that the algorithm exploits new information more quickly rather than waiting for a complete scan of the data before parameters are updated by an M-step. Another method suggested by Neal and Hinton (1998) is the sparse EM (SPEM) algorithm. In fitting a mixture model to a data set by ML via the EM algorithm, the current estimates of some posterior probabilities $ \tau_{ij}^{(k)}$ for a given data point  $ \boldsymbol{y}_j$ are often close to zero. For example, if $ \tau_{ij}^{(k)} < 0.005$ for the first two components of a four-component mixture being fitted, then with the SPEM algorithm we would fix $ \tau_{ij}^{(k)}$ ($ i = 1,2$) for membership of $ \boldsymbol{y}_j$ with respect to the first two components at their current values and only update $ \tau_{ij}^{(k)}$ ($ i=3,4$) for the last two components. This sparse E-step will take time proportional to the number of components that needed to be updated. A sparse version of the IEM algorithm (SPIEM) can be formulated by combining the partial E-step and the sparse E-step. With these versions, the likelihood is still increased after each scan. Ng and McLachlan (2003a) study the relative performances of these algorithms with various number of blocks $ B$ for the fitting of normal mixtures. They propose to choose $ B$ to be that factor of $ n$ that is the closest to $ B^{\ast}=$round$ (n^{2/5})$ for unrestricted component-covariance matrices, where round$ (r)$ rounds $ r$ to the nearest integer.

Other approaches for speeding up the EM algorithm for mixtures have been considered in Bradley et al. (1998) and Moore (1999). The former developed a scalable version of the EM algorithm to handle very large databases with a limited memory buffer. It is based on identifying regions of the data that are compressible and regions that must be maintained in memory. Moore (1999) has made use of multiresolution $ k$d-trees $ (mrk$d-trees) to speed up the fitting process of the EM algorithm on normal mixtures. Here $ k$d stands for $ k$-dimensional where, in our notation, $ k=p$, the dimension of an observation $ \boldsymbol{y}_j$. His approach builds a multiresolution data structure to summarize the database at all resolutions of interest simultaneously. The $ mrk$d-tree is a binary tree that recursively splits the whole set of data points into partitions. The contribution of all the data points in a tree node to the sufficient statistics is simplified by calculating at the mean of these data points to save time. Ng and McLachlan (2003b) combined the IEM algorithm with the $ mrk$d-tree approach to further speed up the EM algorithm. They also studied the convergence properties of this modified version and the relative performance with some other variants of the EM algorithm for speeding up the convergence for the fitting of normal mixtures.

Neither the scalable EM algorithm nor the $ mrk$d-tree approach guarantee the desirable reliable convergence properties of the EM algorithm. Moreover, the scalable EM algorithm becomes less efficient when the number of components $ g$ is large, and the $ mrk$d-trees-based algorithms slow down as the dimension $ p$ increases; see for example Ng and McLachlan (2003b) and the references therein. Further discussion on data mining applications can be found in Chap. III.13 of this handbook.

next up previous contents index
Next: 5.5 Miscellaneous Topics on Up: 5. The EM Algorithm Previous: 5.3 Examples of the