Subsections

• 5.3.1 Example 1: Normal Mixtures
• 5.3.2 Example 2: Censored Failure-Time Data
• 5.3.3 Example 3: Nonapplicability of EM Algorithm
• 5.3.4 Starting Values for EM Algorithm
• 5.3.5 Provision of Standard Errors

5.3 Examples of the EM Algorithm

5.3.1 Example 1: Normal Mixtures

One of the classical formulations of the two-group discriminant analysis or the statistical pattern recognition problem involves a mixture of two $p$-dimensional normal distributions with a common covariance matrix. The problem of two-group cluster analysis with multiple continuous observations has also been formulated in this way. Here, we have $n$ independent observations $\mathbf{y}_1, \mathbf{y}_2, \ldots,$ $\mathbf{y}_n$ from the mixture density

$$\notag (1-\pi) \phi(\mathbf{y}; \mathbf{\mu}_1,\mathbf{\Sigma}) + \pi \phi(\mathbf{y}; \mathbf{\mu}_2,\mathbf{\Sigma})\,,$$

where $\phi(\mathbf{y}; \mathbf{\mu}_i, \mathbf{\Sigma})$ denotes the $p$-dimensional normal density function with mean vector $\mathbf{\mu}_i$ and common covariance matrix $\mathbf{\Sigma}$, $i = 1,2$. The $(1-\pi)$ and $\pi$ denote the proportions of the two clusters, respectively. The problem of estimating the parameters $\mathbf{\Psi} = (\pi, \mathbf{\mu}_1,$ $\mathbf{\mu}_2,$ $\mathbf{\Sigma})$ is an instance of the problem of resolution of mixtures or in pattern recognition parlance an ''unsupervised learning problem''. The MLE problem here is quite messy and classical statistical and pattern recognition literature has struggled with it for a long time.

Consider the corresponding ''supervised learning problem'', where observations on the random vector $\mathbf{X} = (Z, \mathbf{Y})$ are $\mathbf{x}_1 = (z_1, \mathbf{y}_1),$ $\mathbf{x}_2 = (z_2, \mathbf{y}_2), \ldots,$ $\mathbf{x}_n = (z_n, \mathbf{y}_n)$. Here $z_j$ is an indicator variable which identifies the $j$th observation as coming from the first $(z=0)$ or the second $(z=1)$ component $(j=1,\ldots,n)$. The MLE problem is far simpler here with easy closed-form MLE. The classificatory variable $z_j$ could be called the ''missing variable'' and data $\mathbf{z}=(z_1,z_2,\ldots,z_n)^{\top}$ the missing data. The unsupervised learning problem could be called the incomplete-data problem and the supervised learning problem the complete-data problem. A relatively simple iterative method for computing the MLE for the unsupervised problem could be given exploiting the simplicity of the MLE for the supervised problem. This is the essence of the EM algorithm.

The complete-data log likelihood function for $\mathbf{\Psi}$ is given by

$$\log L_c(\mathbf{\Psi}) = \sum_{j=1}^{n} (1-z_j) \log \phi(\mathb... ...\mathbf{\Sigma}) + z_j \log \phi(\mathbf{y}; \mathbf{\mu}_2,\mathbf{\Sigma})\,.$$ (5.10)

By differentiating (5.10) with respect to $\mathbf{\Psi}$, the MLEs of $\mathbf{\Psi}$ are obtained, as if $\mathbf{z}$ were actually observed:

$$\pi = \sum_{j=1}^{n} z_j /n,$$ (5.11)

$$\mathbf{\mu}_1 = \sum_{j=1}^{n} (1-z_j) \mathbf{y}_j \Bigg/ \left(n-\sum_{j=1}^{... ...d \mathbf{\mu}_2 = \sum_{j=1}^{n} z_j \mathbf{y}_j \Bigg/ \sum_{j=1}^{n} z_j\,,$$ (5.12)

$$\mathbf{\Sigma} = \sum_{j=1}^{n} \left[(1-z_j) (\mathbf{y}_j-\mathbf{\mu}_1)(\mat... ...athbf{y}_j-\mathbf{\mu}_2)(\mathbf{y}_j-\mathbf{\mu}_2)^{\top}\right]\Big/ n\,,$$ (5.13)

Now the EM algorithm for this problem starts with some initial value $\mathbf{\Psi}^{(0)}$ for the parameters. As $\log L_c(\mathbf{\Psi})$ in (5.10) is a linear function of the unobservable data  $\mathbf{z}$ for this problem, the calculation of $Q(\mathbf{\Psi}; \mathbf{\Psi}^{(k)})$ on the E-step is effected simply by replacing $z_j$ by its current conditional expectation given the observed data $\mathbf{y}$, which is the usual posterior probability of the $j$th observation arising from component 2

$$\notag \tau_j^{(k)} = E_{\mathbf{\Psi}^{(k)}}(Z_j\vert\mathbf{y})... ...} \phi\left(\mathbf{y}_j; \mathbf{\mu}_2^{(k)},\mathbf{\Sigma}^{(k)}\right)}\,.$$

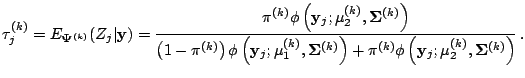The M-step then consists of substituting these $\tau_j^{(k)}$ values for $z_j$ in (5.11) to (5.13). The E- and M-steps are then iterated until convergence. Unlike in the MLE for the supervised problem, in the M-step of the unsupervised problem, the posterior probabilities $\tau_j$, which are between 0 and 1, are used. The mean vectors $\mathbf{\mu}_i \ (i=1,2)$ and the covariance matrix $\mathbf{\Sigma}$ are computed using the $\tau_j^{(k)}$ as weights in weighted averages.

It is easy to extend the above method to a mixture of $g > 2$ multinormal mixtures or even to a mixture of $g > 2$ distributions from other (identifiable) families. For a detailed discussion of the applications of the EM algorithm in the resolution of finite mixtures and other issues of finite mixtures, see McLachlan and Peel (2000).

5.3.2 Example 2: Censored Failure-Time Data

In survival or reliability analyses, the focus is the distribution of time $T$ to the occurrence of some event that represents failure (for computational methods in survival analysis see also Chap. III.12). In many situations, there will be individuals who do not fail at the end of the study, or individuals who withdraw from the study before it ends. Such observations are censored, as we know only that their failure times are greater than particular values. We let $\mathbf{y}=(c_1,\delta_1,\ldots,c_n,\delta_n)^{\top}$ denote the observed failure-time data, where $\delta_j=0$ or $1$ according as the $j$th observation $T_j$ is censored or uncensored at $c_j \ (j=1,\ldots,n)$. That is, if $T_j$ is uncensored, $t_j=c_j$, whereas if $t_j>c_j$, it is censored at $c_j$.

In the particular case where the p.d.f. for $T$ is exponential with mean $\mu$, we have

$$f(t; \mu) = \mu^{-1} \exp\left(-t/\mu\right) I_{(0,\infty)}(t) \qquad (\mu>0)\,,$$ (5.14)

where the indicator function $I_{(0,\infty)}(t)=1$ for $t>0$ and is zero elsewhere. The unknown parameter vector $\mathbf{\Psi}$ is now a scalar, being equal to $\mu$. Denote by $s$ the number of uncensored observations. By re-ordering the data so that the uncensored observations precede censored observations. It can be shown that the log likelihood function for $\mu$ is given by

$$\log L(\mu) = -s \log \mu - \sum_{j=1}^{n} c_j / \mu\,.$$ (5.15)

By equating the derivative of (5.15) to zero, the MLE of $\mu$ is

$$\widehat{\mu} = \sum_{j=1}^{n} c_j / s\,.$$ (5.16)

Thus there is no need for the iterative computation of $\widehat{\mu}$. But in this simple case, it is instructive to demonstrate how the EM algorithm would work and how its implementation could be simplified as the complete-data log likelihood belongs to the regular exponential family (see Sect. 5.2.1).

The complete-data vector $\mathbf{x}$ can be declared to be $\mathbf{x}=(t_1,\ldots,t_s,\mathbf{z}^{\top})^{\top},$ where $\mathbf{z}=(t_{s+1},\ldots,t_n)^{\top}$ contains the unobservable realizations of the $n-s$ censored random variables. The complete-data log likelihood is given by

$$\log L_c(\mu) = -n \log \mu - \sum_{j=1}^{n} t_j / \mu\,.$$ (5.17)

As $\log L_c(\mu)$ is a linear function of the unobservable data $\mathbf{z}$, the E-step is effected simply by replacing $\mathbf{z}$ by its current conditional expectation given $\mathbf{y}$. By the lack of memory of the exponential distribution, the conditional distribution of $T_j-c_j$ given that $T_j>c_j$ is still exponential with mean $\mu$. So, we have

$$E_{\mu^{(k)}}(T_j\vert\mathbf{y}) = E_{\mu^{(k)}}(T_j\vert T_j>c_j) = c_j + \mu^{(k)}$$ (5.18)

for $j=s+1,\ldots,n.$ Accordingly, the $Q$-function is given by

$$\notag Q\left(\mu; \mu^{(k)}\right) = -n \log \mu - \mu^{-1} \left\{ \sum_{j=1}^{n} c_j + (n-s)\mu^{(k)} \right\}\, .$$

In the M-step, we have

$$\mu^{(k+1)}=\left. \left\{ \sum_{j=1}^{n} c_j + (n-s)\mu^{(k)}\right\} \right/ n\,.$$ (5.19)

On putting $\mu^{(k+1)}=\mu^{(k)}=\mu^{\ast}$ in (5.19) and solving for $\mu^{\ast}$, we have for $s<n$ that $\mu^{\ast}=\widehat{\mu}$. That is, the EM sequence $\{ \mu^{(k)} \}$ has the MLE $\widehat{\mu}$ as its unique limit point, as $k \to \infty$; see McLachlan and Krishnan (1997, Sect. 1.5.2).

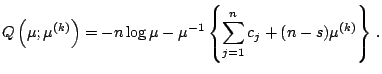From (5.17), it can be seen that $\log L_c(\mu)$ has the exponential family form (5.4) with canonical parameter $\mu^{-1}$ and sufficient statistic $\mathbf{t}(\mathbf{X}) = \sum_{j=1}^{n} T_j.$ Hence, from (5.18), the E-step requires the calculation of $\mathbf{t}^{(k)}= \sum_{j=1}^{n} c_j + (n-s) \mu^{(k)}$. The M-step then yields $\mu^{(k+1)}$ as the value of $\mu$ that satisfies the equation

$$\notag \mathbf{t}^{(k)} = E_{\mu} \{ \mathbf{t}(\mathbf{X}) \} = n\mu\,.$$

This latter equation can be seen to be equivalent to (5.19), as derived by direct differentiation of the $Q$-function.

5.3.3 Example 3: Nonapplicability of EM Algorithm

Examples 1 and 2 may have given an impression that the E-step consists in replacing the missing data by their conditional expectations given the observed data at current parameter values. Although in many examples this may be the case as $\log L_c(\mathbf{\Psi})$ is a linear function of the missing data $\mathbf{z}$, it is not quite so in general. Rather, as should be clear from the general theory described in Sect. 5.2.1, the E-step consists in replacing $\log L_c(\mathbf{\Psi})$ by its conditional expectation given the observed data at current parameter values. Flury and Zoppé (2000) give the following interesting example to demonstrate the point that the E-step does not always consist in plugging in ''estimates'' for missing data. This is also an example where the E-step cannot be correctly executed at all since the expected value of the complete-data log likelihood does not exist, showing thereby that the EM algorithm is not applicable to this problem, at least for this formulation of the complete-data problem.

Let the lifetimes of electric light bulbs of a certain type have a uniform distribution in the interval $(0, \theta]$, $\theta > 0$ and unknown. A total of $n+m$ bulbs are tested in two independent experiments. The observed data consist of $\mathbf{y} = (y_1, \ldots, y_n)$ and $\mathbf{e}= (e_{n+1}, \ldots, e_{n+m})$, where $\mathbf{y}$ are exact lifetimes of a random sample of $n$ bulbs and $\mathbf{e}$ are indicator observations on a random sample of $m$ bulbs, taking value 1 if the bulb is still burning at a fixed time point $T>0$ and 0 if it is expired. The missing data is $\mathbf{z}=(y_{n+1},\ldots,y_{n+m})^{\top}$. Let $s$ be the number of $e_j$'s with value 1 and $y_{\max} = \max\{y_1, \ldots, y_n\}$.

In this example, the unknown parameter vector $\mathbf{\Psi}$ is a scalar, being equal to $\theta$. Let us first work out the MLE of $\theta$ directly. The likelihood is

$$\notag L(\theta) = \theta^{-n} I_{[y_{\max}, \infty)} (\theta) \t... ...(T, \theta)}}\right)^{m-s} \left(1-\frac{{T} }{ {\max(T,\theta)}}\right)^{s}\,,$$

where $I_A$ is the notation for the indicator function of set $A$. For $s = 0$, $L(\theta )$ is decreasing in $\theta$ for $\theta \geq y_{\max}$ and hence the MLE is $\widehat{\theta} = y_{\max}$. For $s \geq 1$, we have $\max(T,\theta)=\theta$. Here the function $L_1(\theta) = (\theta)^{-(n+m)}(\theta - T)^s$ has a unique maximum at $\tilde{\theta} = \frac{{n+m} }{ {n+m-s}} T$ and is monotonically decreasing for $\theta > \tilde{\theta}$. Hence the MLE of $\theta$ is

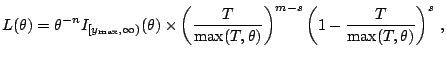$$\notag \widehat{\theta} = \begin{cases}\tilde{\theta} & \mbox{if}... ...\geq 1\\ [-1mm] y_{\max} & \mbox{otherwise}\,. \end{cases}%\end{array} \right.$$

Now let us try the EM algorithm for the case $s \geq 1$. The complete data can be formulated as $y_1,\ldots,y_n,y_{n+1},\ldots,y_{n+m}$ and the complete-data MLE is

$$\notag \max_{j=1, \ldots, n+m} y_j\,.$$

Since $s \geq 1$, we have $\theta \geq T$. Now if we take the approach of replacing the missing observations, then we compute

$$\notag E_{\theta^{(k)}}\left(y_j^{(k+1)}\vert\mathbf{y}, \mathbf{... ...splaystyle\frac{1}{2} T & \mbox{if}\; e_j =0 \end{cases}%\end{array} \right.$$$$

for $j = n+1, \ldots, n+m.$ The M-step is

$$\notag \theta^{(k+1)} = \max \left\{y_{\max}, {\frac{1}{2}} \left(T+\theta^{(k)}\right)\right\}.$$

Combining the E- and M-steps, we can write the EM algorithm as a sequence of iterations of the equation

$$\notag \theta^{(k+1)} = \mathbf{M}\left(\theta^{k}\right) \equiv \max\left\{y_{\max}, {\frac{1}{2}}\left(T+\theta^{(k)}\right)\right\}\,.$$

It is easily seen that if we start with any $\theta^{(0)}$, this procedure will converge to $\widehat{\theta} = \max\{y_{\max}, T\}$, by noting that $\widehat{\theta}= \mathbf{M}(\widehat{\theta})$.

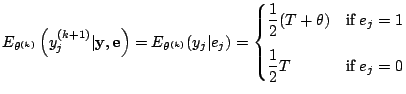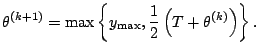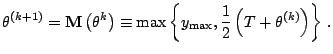The reason for the apparent EM algorithm not resulting in the MLE is that the E-step is wrong. In the E-step, we are supposed to find the conditional expectation of $\log L_c(\theta)$ given $\mathbf{y}, \mathbf{e}$ at current parameter values. Now given the data with $s \geq 1$, we have $\theta \geq T$ and hence the conditional distributions of $y_j$ are uniform in $[T, \theta^{(k)}]$. Thus for $\theta < \theta^{(k)}$ the conditional density of missing $y_j$ takes value 0 with positive probability and hence the conditional expected value of the complete-data log likelihood we are seeking does not exist.

5.3.4 Starting Values for EM Algorithm

The EM algorithm will converge very slowly if a poor choice of initial value $\mathbf{\Psi}^{(0)}$ were used. Indeed, in some cases where the likelihood is unbounded on the edge of the parameter space, the sequence of estimates $\{ \mathbf{\Psi}^{(k)} \}$ generated by the EM algorithm may diverge if $\mathbf{\Psi}^{(0)}$ is chosen too close to the boundary. Also, with applications where the likelihood equation has multiple roots corresponding to local maxima, the EM algorithm should be applied from a wide choice of starting values in any search for all local maxima. A variation of the EM algorithm (Wright and Kennedy, 2000) uses interval analysis methods to locate multiple stationary points of a log likelihood within any designated region of the parameter space.

Here, we illustrate different ways of specification of initial value within mixture models framework. For independent data in the case of mixture models of $g$ components, the effect of the E-step is to update the posterior probabilities of component membership. Hence the first E-step can be performed by specifying a value $\mathbf{\tau}_j^{(0)}$ for each $j \ \left(j=1,\ldots,n\right)$, where $\mathbf{\tau}_j = (\tau_{1j},\ldots,\tau_{gj})^{\top}$ is the vector containing the $g$ posterior probabilities of component membership for $\mathbf{y}_j$. The latter is usually undertaken by setting $\mathbf{\tau}_j^{(0)}=\mathbf{z}_j^{(0)}$, where

$$\notag \mathbf{z}^{(0)}=\left({\mathbf{z}_1^{(0)}}^{\top},\ldots,{\mathbf{z}_n^{(0)}}^{\top}\right)^{\top}$$

defines an initial partition of the data into $g$ components. For example, an ad hoc way of initially partitioning the data in the case of, say, a mixture of $g=2$ normal components with the same covariance matrices (Example 1, Sect. 5.3.1) would be to plot the data for selections of two of the $p$ variables, and then draw a line that divides the bivariate data into two groups that have a scatter that appears normal. For higher-dimensional data, an initial value $\mathbf{z}^{(0)}$ for $\mathbf{z}$ might be obtained through the use of some clustering algorithm, such as $k$-means or, say, an hierarchical procedure if $n$ is not too large.

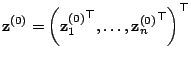Another way of specifying an initial partition $\mathbf{z}^{(0)}$ of the data is to randomly divide the data into $g$ groups corresponding to the $g$ components of the mixture model. With random starts, the effect of the central limit theorem tends to have the component parameters initially being similar at least in large samples. One way to reduce this effect is to first select a small random subsample from the data, which is then randomly assigned to the $g$ components. The first M-step is then performed on the basis of the subsample. The subsample has to be sufficiently large to ensure that the first M-step is able to produce a nondegenerate estimate of the parameter vector $\mathbf{\Psi}$ (McLachlan and Peel, 2000, Sect. 2.12). In the context of $g$ normal components, a method of specifying a random start is to generate the means $\mathbf{\mu}_i^{(0)}$ independently as

$$\notag \mathbf{\mu}_1^{(0)},\ldots,\mathbf{\mu}_g^{(0)} \stackrel{i.i.d.}{\sim} N(\bar{\mathbf{y}},\mathbf{V})\,,$$

where $\bar{\mathbf{y}}$ is the sample mean and $\mathbf{V} = \sum_{j=1}^{n} (\mathbf{y}_j - \bar{\mathbf{y}})(\mathbf{y}_j - \bar{\mathbf{y}})^{\top}/n$ is the sample covariance matrix of the observed data. With this method, there is more variation between the initial values $\mathbf{\mu}_i^{(0)}$ for the component means $\mathbf{\mu}_i$ than with a random partition of the data into $g$ components. The component-covariance matrices $\mathbf{\Sigma}_i$ and the mixing proportions $\pi_i$ can be specified as

$$\notag \mathbf{\Sigma}_i^{(0)} = \mathbf{V} \pi_i^{(0)} = 1/g \quad (i=1,\ldots,g)\,.$$

Ueda and Nakano (1998) considered a deterministic annealing EM (DAEM) algorithm in order for the EM iterative process to be able to recover from a poor choice of starting value. They proposed using the principle of maximum entropy and the statistical mechanics analogy, whereby a parameter, say $\theta$, is introduced with $1/ \theta$ corresponding to the ''temperature'' in an annealing sense. With their DAEM algorithm, the E-step is effected by averaging $\log L_c(\mathbf{\Psi})$ over the distribution taken to be proportional to that of the current estimate of the conditonal density of the complete data (given the observed data) raised to the power of $\theta$; see for example McLachlan and Peel (2000, pp. 58-60).

5.3.5 Provision of Standard Errors

Several methods have been suggested in the EM literature for augmenting the EM computation with some computation for obtaining an estimate of the covariance matrix of the computed MLE. Many such methods attempt to exploit the computations in the EM steps. These methods are based on the observed information matrix $\mathbf{I}(\widehat{\mathbf{\Psi}}; \mathbf{y})$, the expected information matrix $\mathcal{I}(\mathbf{\Psi})$ or on resampling methods. Baker (1992) reviews such methods and also develops a method for computing the observed information matrix in the case of categorical data. Jamshidian and Jennrich (2000) review more recent methods including the Supplemented EM (SEM) algorithm of Meng and Rubin (1991) and suggest some newer methods based on numerical differentiation.

Theorectically one may compute the asymptotic covariance matrix by inverting the observed or expected information matrix at the MLE. In practice, however, this may be tedious analytically or computationally, defeating one of the advantages of the EM approach. Louis (1982) extracts the observed information matrix in terms of the conditional moments of the gradient and curvature of the complete-data log likelihood function introduced within the EM framework. These conditional moments are generally easier to work out than the corresponding derivatives of the incomplete-data log likelihood function. An alternative approach is to numerically differentiate the likelihood function to obtain the Hessian. In a EM-aided differentiation approach, Meilijson (1989) suggests perturbation of the incomplete-data score vector to compute the observed information matrix. In the SEM algorithm (Meng and Rubin, 1991), numerical techniques are used to compute the derivative of the EM operator $\mathbf{M}$ to obtain the observed information matrix. The basic idea is to use the fact that the rate of convergence is governed by the fraction of the missing information to find the increased variability due to missing information to add to the assessed complete-data covariance matrix. More specifically, let $\mathbf{V}$ denote the asymptotic covariance matrix of the MLE $\widehat{\mathbf{\Psi}}$. Meng and Rubin (1991) show that

$$\mathbf{I}^{-1}\left(\widehat{\mathbf{\Psi}}; \mathbf{y}\right) =... ...left(\widehat{\mathbf{\Psi}}; \mathbf{y}\right) + \mathrm{\Delta} \mathbf{V}\,,$$ (5.20)

where $\mathrm{\Delta} \mathbf{V} = \{ \mathbf{I}_d - \mathbf{J}(\widehat{\mathbf{\Ps... ...idehat{\mathbf{\Psi}}) \mathcal{I}_c^{-1}(\widehat{\mathbf{\Psi}}; \mathbf{y})$ and $\mathcal{I}_c (\widehat{\mathbf{\Psi}}; \mathbf{y})$ is the conditional expected complete-data information matrix, and where $\mathbf{I}_d$ denotes the $d \times d$ identity matrix. Thus the diagonal elements of $\mathrm{\Delta} \mathbf{V}$ give the increases in the asymptotic variances of the components of $\widehat{\mathbf{\Psi}}$ due to missing data. For a wide class of problems where the complete-data density is from the regular exponential family, the evaluation of $\mathcal{I}_c (\widehat{\mathbf{\Psi}}; \mathbf{y})$ is readily facilitated by standard complete-data computations (McLachlan and Krishnan, 1997, Sect. 4.5). The calculation of $\mathbf{J}(\widehat{\mathbf{\Psi}})$ can be readily obtained by using only EM code via numerically differentiation of $\mathbf{M}(\mathbf{\Psi})$. Let $\widehat{\mathbf{\Psi}}= \mathbf{\Psi}^{(k+1)}$ where the sequence of EM iterates has been stopped according to a suitable stopping rule. Let $M_i$ be the $i$th component of $\mathbf{M}(\mathbf{\Psi})$. Let $\mathbf{u}^{(j)}$ be a column $d$-vector with the $j$th coordinate $1$ and others 0. With a possibly different EM sequence $\mathbf{\Psi}^{(k)}$, let $r_{ij}$ be the $(i,j)$th element of $\mathbf{J}(\widehat{\mathbf{\Psi}})$, we have

$$\notag r_{ij}^{(k)} = \frac{{M_i\left[\widehat{\mathbf{\Psi}} + \... ...{\mathbf{\Psi}}_i } }{ {\mathbf{\Psi}_j^{(k)} - \widehat{\mathbf{\Psi}}_j} }\,.$$

Use a suitable stopping rule like $\vert r_{ij}^{(k+1)} - r_{ij}^{(k)}\vert < \sqrt{\epsilon}$ to stop each of the sequences $r_{ij} \ (i,j = 1, 2, \ldots, d)$ and take $r_{ij}^{\ast} = r_{ij}^{(k+1)}$; see McLachlan and Krishnan (1997, Sect. 4.5).

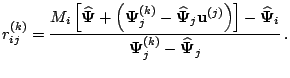It is important to emphasize that estimates of the covariance matrix of the MLE based on the expected or observed information matrices are guaranteed to be valid inferentially only asymptotically. In particular for mixture models, it is well known that the sample size $n$ has to be very large before the asymptotic theory of maximum likelihood applies. A resampling approach, the bootstrap (Efron, 1979; Efron and Tibshirani, 1993), has been considered to tackle this problem. Basford et al. (1997) compared the bootstrap and information-based approaches for some normal mixture models and found that unless the sample size was very large, the standard errors obtained by an information-based approach were too unstable to be recommended.

The bootstrap is a powerful technique that permits the variability in a random quantity to be assessed using just the data at hand. Standard error estimation of $\widehat{\mathbf{\Psi}}$ may be implemented according to the bootstrap as follows. Further discussion on bootstrap and resampling methods can be found in Chaps. III.2 and III.3 of this handbook.

1. A new set of data, $\mathbf{y}^{\ast}$, called the bootstrap sample, is generated according to $\widehat{F}$, an estimate of the distribution function of $\mathbf{Y}$ formed from the original observed data $\mathbf{y}$. That is, in the case where $\mathbf{y}$ contains the observed values of a random sample of size $n$, $\mathbf{y}^{*}$ consists of the observed values of the random sample

   $$\notag \mathbf{Y}_1^{*}, \ldots, \mathbf{Y}_n^{\ast}\; \mathop{\sim}\limits^{\text{i.i.d.}}\,\widehat{F}\,,$$

   
   
   where the estimate $\widehat{F}$ (now denoting the distribution function of a single observation $\mathbf{Y}_j$) is held fixed at its observed value.
2. The EM algorithm is applied to the bootstrap observed data $\mathbf{y}^{\ast}$ to compute the MLE for this data set, $\widehat{\mathbf{\Psi}}^{\ast}$.
3. The bootstrap covariance matrix of $\widehat{\mathbf{\Psi}}^{\ast}$ is given by

   $$^{\ast}(\widehat{\mathbf{\Psi}}^{\ast})=E^{\ast}\left[\left\{\wid... ...t}-E^{\ast}\left(\widehat{\mathbf{\Psi}}^{\ast}\right)\right\}^{\top}\right]\,,$$ (5.21)

   
   
   where $E^{\ast}$ denotes expectation over the bootstrap distribution specified by $\widehat{F}$.

The bootstrap covariance matrix can be approximated by Monte Carlo methods. Steps 1 and 2 are repeated independently a number of times (say, $B$) to give $B$ independent realizations of $\widehat{\mathbf{\Psi}}^{\ast}$, denoted by $\widehat{\mathbf{\Psi}}_1^{\ast}, \ldots, \widehat{\mathbf{\Psi}}_B^{\ast}$. Then (5.21) can be approximated by the sample covariance matrix of these $B$ bootstrap replications to give

$$^{\ast}\left(\widehat{\mathbf{\Psi}}^{\ast}\right) \approx \sum_{... ...i}}_b^{\ast}-{\overline{\widehat{\mathbf{\Psi}}}}^{\ast}\right)^{\top}/(B-1)\,,$$ (5.22)

where ${\overline{\widehat{\mathbf{\Psi}}}}^{\ast}=\sum_{b=1}^B\widehat{\mathbf{\Psi}}_b^{\ast}/B.$ The standard error of the $i$th element of $\widehat{\mathbf{\Psi}}$ can be estimated by the positive square root of the $i$th diagonal element of (5.22). It has been shown that 50 to 100 bootstrap replications are generally sufficient for standard error estimation (Efron and Tibshirani, 1993).

In Step 1 above, the nonparametric version of the bootstrap would take $\widehat{F}$ to be the empirical distribution function formed from the observed data $\mathbf{y}$. Situations where we may wish to use the latter include problems where the observed data are censored or are missing in the conventional sense. In these cases the use of the nonparametric bootstrap avoids having to postulate a suitable model for the underlying mechanism that controls the censorship or the absence of the data. A generalization of the nonparametric version of the bootstrap, known as the weighted bootstrap, has been studied by Newton and Raftery (1994).