Given their recent popularity and clear evidence of wide applicability the most of the space in this chapter is devoted to Wavelet transforms. Statistical multiscale modeling has, in recent decade, become a well established area in both theoretical and applied statistics, with impact to developments in statistical methodology.
Wavelet-based methods are important in statistics in areas such as regression, density and function estimation, factor analysis, modeling and forecasting in time series analysis, in assessing self-similarity and fractality in data, in spatial statistics.
The attention of the statistical community was attracted in late 1980's and early 1990's, when Donoho, Johnstone, and their coauthors demonstrated that wavelet thresholding, a simple denoising procedure, had desirable statistical optimality properties. Since then, wavelets have proved useful in many statistical disciplines, notably in nonparametric statistics and time series analysis. Bayesian concepts and modeling approaches have, more recently, been identified as providing promising contexts for wavelet-based denoising applications.
In addition to replacing traditional orthonormal bases in a variety statistical problems, wavelets brought novel techniques and invigorated some of the existing ones.
We start first with a statistical application of wavelet transforms. This example emphasizes specificity of wavelet-based denoising not shared by standard state-of-art denoising techniques.
A researcher in geology was interested in predicting earthquakes by
the level of water in nearby wells. She had a large (
![]() measurements) data set of water levels taken every hour in a period of
time of about one year in a California well. Here is the description
of the problem.
measurements) data set of water levels taken every hour in a period of
time of about one year in a California well. Here is the description
of the problem.
The ability of water wells to act as strain meters has been observed for centuries. The Chinese, for example, have records of water flowing from wells prior to earthquakes. Lab studies indicate that a seismic slip occurs along a fault prior to rupture. Recent work has attempted to quantify this response, in an effort to use water wells as sensitive indicators of volumetric strain. If this is possible, water wells could aid in earthquake prediction by sensing precursory earthquake strain.
We have water level records from six wells in southern California, collected over a six year time span. At leastmoderate size earthquakes (magnitude
-
) occurred in close proximity to the wells during this time interval. There is a significant amount of noise in the water level record which must first be filtered out. Environmental factors such as earth tides and atmospheric pressure create noise with frequencies ranging from seasonal to semidiurnal. The amount of rainfall also affects the water level, as do surface loading, pumping, recharge (such as an increase in water level due to irrigation), and sonic booms, to name a few. Once the noise is subtracted from the signal, the record can be analyzed for changes in water level, either an increase or a decrease depending upon whether the aquifer is experiencing a tensile or compressional volume strain, just prior to an earthquake.
A plot of the raw data for hourly measurements over one year
(
![]() observations) is given in Fig. 7.6a, with
a close-up in Fig. 7.6b. After applying the wavelet
transform and further processing the wavelet
coefficients (thresholding), we obtained a fairly clean signal with
a big jump at the earthquake time. The wavelet-denoised data are given
in Fig. 7.6d. The magnitude of the water level change at
the earthquake time did not get distorted in contrast to traditional
smoothing techniques. This local adaptivity is a desirable feature of
wavelet methods.
observations) is given in Fig. 7.6a, with
a close-up in Fig. 7.6b. After applying the wavelet
transform and further processing the wavelet
coefficients (thresholding), we obtained a fairly clean signal with
a big jump at the earthquake time. The wavelet-denoised data are given
in Fig. 7.6d. The magnitude of the water level change at
the earthquake time did not get distorted in contrast to traditional
smoothing techniques. This local adaptivity is a desirable feature of
wavelet methods.
For example, Fig. 7.6c, is denoised signal after applying supsmo smoothing procedure. Note that the earthquake jump is smoothed, as well.
![\includegraphics[width=4.7cm]{text/2-7/e1.eps}](img2529.gif) (a) (a)
![\includegraphics[width=4.7cm]{text/2-7/closee.eps}](img2530.gif) (b) (b)
![\includegraphics[width=4.7cm]{text/2-7/supersmo.eps}](img2531.gif) (c) (c)
![\includegraphics[width=4.7cm]{text/2-7/e4.eps}](img2532.gif) (d) (d)
|
The first theoretical results in wavelets had been concerned with continuous wavelet decompositions of functions and go back to the early 1980s. Papers of Morlet et al. (1982)[19] and Grossmann and Morlet (1984, 1985)[13,14] were among the first on this subject.
Let
![]() ,
,
![]() be
a family of functions defined as translations and re-scales of
a single function
be
a family of functions defined as translations and re-scales of
a single function
![]() ,
,
Normalization constant
![]() ensures that the norm
ensures that the norm
![]() is independent of
is independent of ![]() and
and ![]() The
function
The
function ![]() (called the wavelet function) is assumed to
satisfy the admissibility condition,
(called the wavelet function) is assumed to
satisfy the admissibility condition,
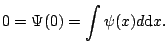 |
Wavelet functions are usually normalized to ''have unit energy'',
i.e.,
![]() .
.
For example, the second derivative of the Gaussian function,
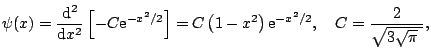 |
For any square integrable function ![]() , the continuous wavelet
transform is defined as a function of two variables
, the continuous wavelet
transform is defined as a function of two variables
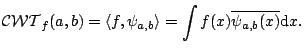 |
Figure 7.8 gives the doppler test function,
![]() ,
,
![]() , and its continuous wavelet transform.
The wavelet used was Mexican Hat. Notice the distribution of
''energy'' in the time/frequency plane in Fig. 7.8b.
, and its continuous wavelet transform.
The wavelet used was Mexican Hat. Notice the distribution of
''energy'' in the time/frequency plane in Fig. 7.8b.
![\includegraphics[width=7.5cm]{text/2-7/doppler.eps}](img2554.gif) (a) (a)
![\includegraphics[width=7.5cm]{text/2-7/dopplerc.eps}](img2555.gif) (b) (b)
|
When the admissibility condition is satisfied, i.e.,
![]() , it is possible to find the inverse continuous transform via
the relation known as resolution of identity or
Calderón's reproducing identity,
, it is possible to find the inverse continuous transform via
the relation known as resolution of identity or
Calderón's reproducing identity,
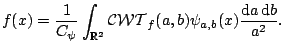 |
The continuous wavelet transform of a function of one variable is
a function of two variables. Clearly, the transform is redundant. To
''minimize'' the transform one can select discrete values of ![]() and
and ![]() and still have a lossless transform. This is achieved by so
called critical sampling.
and still have a lossless transform. This is achieved by so
called critical sampling.
The critical sampling defined by
Fundamental for construction of critically sampled orthogonal wavelets
is a notion of multiresolution analysis introduced by Mallat (1989a,
1989b)[16,17]. A multiresolution analysis (MRA)
is a sequence of closed subspaces
![]() in
in
![]() such that they lie in a containment hierarchy
such that they lie in a containment hierarchy
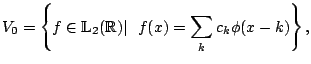 |
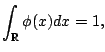 |
The coefficients ![]() in (7.21) are important in efficient
application of wavelet transforms. The (possibly infinite) vector
in (7.21) are important in efficient
application of wavelet transforms. The (possibly infinite) vector
![]() ,
,
![]() will be called
a wavelet filter. It is a low-pass (averaging) filter as will
become clear later by its analysis in the Fourier domain.
will be called
a wavelet filter. It is a low-pass (averaging) filter as will
become clear later by its analysis in the Fourier domain.
To further explore properties of multiresolution analysis subspaces and their bases, we will often work in the Fourier domain.
It will be convenient to use Fourier domain for subsequent analysis of
wavelet paradigm. Define the function ![]() as follows:
as follows:
In the Fourier domain the relation (7.21) becomes
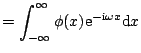 |
||
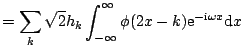 |
||
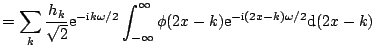 |
||
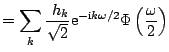 |
||
By iterating (7.23), one gets
Next, we prove two important properties of wavelet filters associated with an orthogonal multiresolution analysis, normalization and orthogonality.
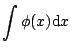 |
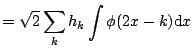 |
|
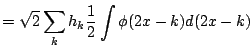 |
||
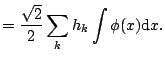 |
This result also follows from
![]() .
.
For any
![]()
![$\displaystyle = 2 \sum_k h_k \left[\sum_m h_m \frac{1}{2} \int \phi(2 x - k) \phi(2 x- 2 l - m) \, {\mathrm{d}}( 2 x ) \right]$](img2613.gif) |
||
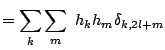 |
||
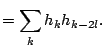 |
An important special case is ![]() for which (7.26) becomes
for which (7.26) becomes
The fact that the system
![]() ,
,
![]() constitutes an orthonormal basis for
constitutes an orthonormal basis for ![]() can be expressed in the
Fourier domain in terms of either
can be expressed in the
Fourier domain in terms of either
![]() or
or
![]() .
.
In terms of
![]() ,
,
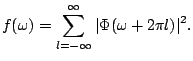 |
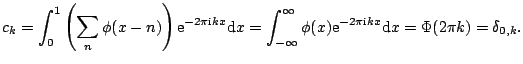 |
Orthogonality condition 7.29 can be expressed in terms of
![]() as:
as:
Since
![]() ,
then by (7.23)
,
then by (7.23)
Now split the sum in (7.33) into two sums - one with odd and the other with even indices, i.e.,
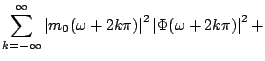 |
||
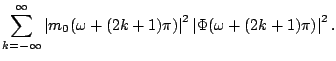 |
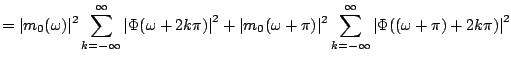 |
||
Whenever a sequence of subspaces satisfies MRA properties, there
exists (though not unique) an orthonormal basis for
![]() ,
,
Next, we discuss the derivation of a wavelet function from the scaling
function. Since
![]() (because of the containment
(because of the containment
![]() ), it can be represented as
), it can be represented as
Define
The spaces ![]() and
and ![]() are orthogonal by construction. Therefore,
are orthogonal by construction. Therefore,
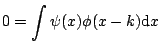 |
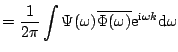 |
|
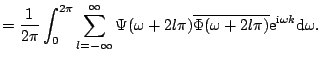 |
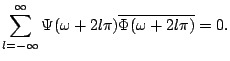 |
By taking into account the definitions of ![]() and
and ![]() , and by the
derivation as in (7.32), we find
, and by the
derivation as in (7.32), we find
From (7.38), we conclude that there exists
a function
![]() such that
such that
To summarize, we choose
![]() such that
such that
Standard choices for
![]() are
are
![]() ,
,
![]() , and
, and
![]() ; however, any other function
satisfying (i)-(iii) will generate a valid
; however, any other function
satisfying (i)-(iii) will generate a valid ![]() . We choose to
define
. We choose to
define
![]() as
as
The form of ![]() and (7.29) imply that
and (7.29) imply that
![]() ,
,
![]() is an orthonormal basis for
is an orthonormal basis for ![]() .
.
Since
![]() , the orthogonality
condition (7.32) can be rewritten as
, the orthogonality
condition (7.32) can be rewritten as
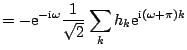 |
||
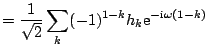 |
||
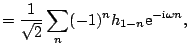 |
In addition to their simplicity and formidable applicability, Haar
wavelets have tremendous educational value.
Here we illustrate some of the relations discussed in the
Sect. 7.3.3 using the Haar wavelet. We start with scaling
function
![]() and pretend that everything
else is unknown. By inspection of simple graphs of two scaled Haar
wavelets
and pretend that everything
else is unknown. By inspection of simple graphs of two scaled Haar
wavelets ![]() and
and
![]() stuck to each other, we
conclude that the scaling equation (7.21) is
stuck to each other, we
conclude that the scaling equation (7.21) is
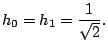 |
The transfer functions are
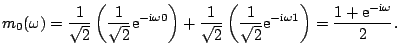 |
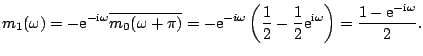 |
Relation (7.37) becomes
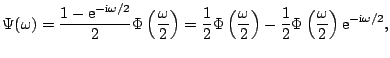 |
Although the Haar wavelets are well localized in the time domain, in
the frequency domain they decay at the slow rate of ![]() and are
not effective in approximating smooth functions.
and are
not effective in approximating smooth functions.
The most important family of wavelets was discovered by Ingrid Daubechies and fully described in Daubechies (1992)[8]. This family is compactly supported with various degrees of smoothness.
The formal derivation of Daubechies' wavelets goes beyond the scope of this chapter, but the filter coefficients of some of its family members can be found by following considerations.
For example, to derive the filter taps of a wavelet with ![]() vanishing
moments, or equivalently,
vanishing
moments, or equivalently, ![]() filter taps, we use the following
equations.
filter taps, we use the following
equations.
The normalization property of scaling function implies
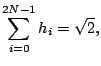 |
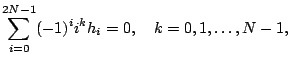 |
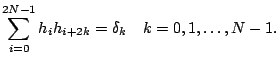 |
We obtained ![]() equations with
equations with ![]() unknowns; however the system
is solvable since the equations are not linearly independent.
unknowns; however the system
is solvable since the equations are not linearly independent.
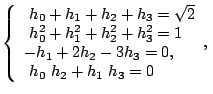 |
For ![]() , the system is
, the system is
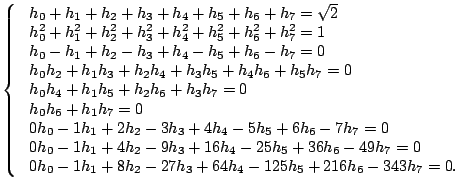 |
Figure 7.9 depicts two scaling function and wavelet pairs from the Daubechies family. Figure 7.9a,b depict the pair with two vanishing moments, while Fig. 7.9c,d depict the pair with four vanishing moments.
![\includegraphics[width=5.4cm]{text/2-7/daub2f.eps}](img2722.gif) (a) (a)
![\includegraphics[width=5.4cm]{text/2-7/daub2m.eps}](img2723.gif) (b) (b)
![\includegraphics[width=5.4cm]{text/2-7/daub4f.eps}](img2724.gif) (c) (c)
![\includegraphics[width=5.4cm]{text/2-7/daub4m.eps}](img2725.gif) (d) (d)
|