9.2 Additive Models with Known Link

It is clear that additive models are just a special case of APLM or GAM (without a parametric linear part and a trivial link function $G =$ identity). The other way around, what we said about the advantages and motivations for additive model holds also for APLM and GAM. In Chapter 5, models with link function have been introduced and motivated, in particular for latent variables or binary choice models. Hence, an additive modeling of the index function is analogous to extending linear regressions models to additive models.

Again it was Stone (1986) who showed that GAM has the favorable property of circumventing the curse of dimensionality. Doing the estimation properly, the rate of convergence can reach the same degree that is typical for the univariate case.

9.2.1 GAM using Backfitting

As we have discussed for additive models, there are two alternative approaches estimating the component functions, backfitting and marginal integration. However, recall that in models with a nontrivial link $G$, the response $Y$ is not directly related to the index function. This fact must now be taken into account in the estimation procedure. For example, consider the partial residual

$${\boldsymbol{r}}_{\alpha}={\boldsymbol{Y}}-\widehat c - \sum_{j \neq \alpha} \widehat{{\boldsymbol{g}}}_j.$$

This ${\boldsymbol{r}}_{\alpha}$ is not appropriate for the generalized model as it ignores the link function $G$. So both methods, backfitting and marginal integration need to be extended for the link function. Instead of using $Y$ we consider a transformation of $Y$, which is essentially the inverse of the link function applied to $Y$.

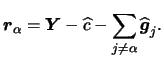
As before, we denote this adjusted dependent variable with $Z$. After conducting a complete backfitting with partial residuals based on $Z$ we obtain a set of estimated functions $\widehat{g}_\alpha (\bullet)$ that explain the variable $Z$. But how good do these functions explain the untransformed dependent variable $Y$? The fit of the overall model in this sense is assessed by the local scoring algorithm. The complete estimation procedure for GAM thus consists of two iterative algorithms: backfitting and local scoring. Backfitting is the ``inner" iteration, whereas local scoring can bee seen as the ``outer" iteration.

We summarized the final algorithm as given by Buja et al. (1989) and Hastie & Tibshirani (1990). For the presentation keep in mind that local scoring corresponds to Fisher scoring in the IRLS algorithm for the GLM. Then, backfitting fits the index by additive instead of linear components. The inner backfitting algorithm is thus completely analogous to that in Chapter 8.

Recall that $V(\bullet)$ is the variance function of $Y$ in a generalized model, see Subsections 5.2.1 and 5.2.3. For the definition of $Z_i$ and $w_i$ we refer to IRLS algorithm in Subsection 5.2.3 and the GPLM algorithms in Chapter 7,

Next, we present the backfitting routine which is applied inside local scoring to fit the additive component functions. This backfitting differs from that in the AM case in that firstly we use the adjusted dependent variable $Z$ instead of $Y$ and secondly we use a weighted smoothing. For this purpose we introduce the weighted smoother matrix ${\mathbf{S}}_\alpha (\bullet \vert {\boldsymbol{w}})$ defined as ${\boldsymbol{D}}^{-1}{\mathbf{S}}_\alpha {\mathbf{W}}$ where ${\mathbf{W}}= \mathop{\hbox{diag}}(w_1,\ldots w_n)^\top$ ($w_i$ from the local scoring) and ${\mathbf{D}}= \mathop{\hbox{diag}}( {\mathbf{S}}_\alpha {\mathbf{W}})$.

Here, we use again vector notation: ${\boldsymbol{r}}_\alpha=(r_{1\alpha},\ldots,r_{n\alpha})^\top$, ${\boldsymbol{Z}}=(Z_{1},\ldots,Z_{n})^\top$, and $\widehat{{\boldsymbol{g}}}_\alpha=(\widehat g_\alpha(X_{1\alpha}),\ldots,g_\alpha(X_{n\alpha}))^\top$.

The theoretical properties of these iterative procedures are even complicated when the index consists of known (up to some parameters) component functions. For the general case of nonparametric index functions asymptotic results have only been be developed for special cases. The situation is different for the marginal integration approach which we study in the following subsection.

9.2.2 GAM using Marginal Integration

When using the marginal integration approach to estimate a GAM, the local scoring loop is not needed. Here, the extension from the additive model to the to GAM is straight forward. Recall that we consider

$$m({\boldsymbol{X}}) = G\left\{ c+\sum_{\alpha =1}^d g_\alpha (X_\alpha ) \right\}$$

with a known link function and existing inverse $G^{-1}$ and only continuous explanatory variables ${\boldsymbol{X}}$. Hence, we can write

$$G^{-1}\left\{ m({\boldsymbol{X}}) \right\} = c+\sum_{\alpha =1}^d g_\alpha (X_\alpha ).$$

As we have seen for the additive model, the component function $g_\alpha (x_\alpha)$ is up to a constant equal to

$$\int G^{-1} \left\{ m(x_\alpha , {\boldsymbol{x}}_{\underline{\al... ...{\boldsymbol{x}}_{\underline{\alpha}}) d {\boldsymbol{x}}_{\underline{\alpha}}$$

when we use the identifying condition $E\{g_\alpha (X_\alpha)\}=0$ for all $\alpha$. Thus we obtain an explicit expression for its estimator by

$$\widehat g_\alpha (x_\alpha ) = \frac 1n \sum_{l=1}^n G^{-1} \lef... ... \widetilde m (X_{i\alpha} ,{\boldsymbol{X}}_{l\underline{\alpha}} ) \right\} .$$ (9.14)

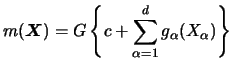
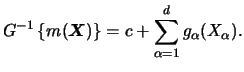
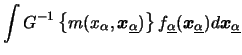
Using a kernel smoother for the pre-estimator $\widetilde m$, this estimator has similar asymptotical properties as we found for the additive model, cf. Subsection 8.2.2. We remark that using a local polynomial smoother for $\widetilde m$ can yield simultaneously estimates for the derivatives of the component functions $g_\alpha$. However, due to the existence of a nontrivial link $G$, all expressions become more complicated. Let us note that for models of the form

$$G^{-1} \{ m({\boldsymbol{x}}) \} = c+ \sum_{\alpha=1}^d g_\alpha (x_\alpha )$$

using the definitions

$$J_v = \{ (j_1,j_2\ldots ,j_v )\vert 0\leq j_1,j_2,\ldots ,j_v \leq v, \ and \ j_1+2j_2+\cdots +vj_v=v \}$$

and

$$\partial^{(\lambda)}_\alpha m({\boldsymbol{t}}) = \partial^\lambda m({\boldsymbol{x}}) / \partial x_\alpha^\lambda,$$

it holds

$$g_\alpha^{(v)} (x_\alpha) = v! \sum_{(j_1,j_2,\ldots ,j_v)\in J_v... ...}}_{\underline{\alpha} ) \}^{j_\lambda}}}{(\lambda !)^{j_\lambda } j_\lambda !}$$ (9.15)

with ${G^{-1}}^{(\kappa)}$ being the $\kappa$th derivative of $G^{-1}$. For example, if we are interested in the first derivative of $g_\alpha$, equation (9.14) with (9.15) gives

$$\widehat g^{(1)}_\alpha (x_\alpha ) = \frac{1}{n} \sum_{l=1}^n {G... ...e \partial^{(1)}_\alpha m(x_\alpha, {\boldsymbol{X}}_{l\underline{\alpha}} ) ,$$

where we used both $\widetilde m$ as well as $\widetilde \partial^{(1)}_\alpha m$, from the local linear or higher order polynomial regression.

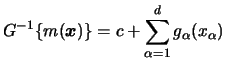
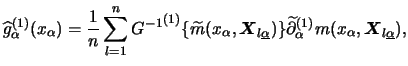
The expression for the second derivative is additionally complicated. Yang et al. (2003) provide asymptotic theory and simulations for this procedure. For the sake of simplicity we restrict the following theorem to the local constant estimation of the pre-estimate $\widetilde m$, see also Linton & Härdle (1996). As introduced previously, the integration estimator requires to choose two bandwidths, $h$ for the direction of interest and $\widetilde{h}$ for the nuisance direction.

THEOREM 9.2  
Assume the bandwidths fulfill $h = O(n^{-1/5})$ and that $n^{2/5} \widetilde{h}^d \to 0$ and $n^{2/5}\widetilde{h}^{d-1} \to \infty$. Then, under smoothness and regularity conditions we have

$$n^{2/5}\left\{ \widehat{g}_\alpha(x_\alpha)-g _\alpha(x_\alpha)\r... ...rrow}\limits_{}^{L}} {N}\left\{ b_\alpha(t_\alpha),v_\alpha(t_\alpha)\right\}.$$

It is obvious that marginal integration leads to estimates of the same rate as for univariate Nadaraya-Watson regression. This is the same rate that we obtained for the additive model without link function. Let us mention that in general the properties of backfitting and marginal integration found in Chapter 8 carry over to the GAM. However, detailed simulation studies do not yet exist for this case and a theoretical comparison is not possible due to the lack of asymptotical results for backfitting in GAM.