The aim of factor analysis is to explain the outcome of
![]() variables in the data matrix
variables in the data matrix ![]() using fewer
variables, the so-called factors.
Ideally all the information in
using fewer
variables, the so-called factors.
Ideally all the information in ![]() can be reproduced by a smaller number of
factors. These factors are interpreted as latent (unobserved)
common characteristics of the observed
can be reproduced by a smaller number of
factors. These factors are interpreted as latent (unobserved)
common characteristics of the observed
![]() .
The case just described occurs when every observed
.
The case just described occurs when every observed
![]() can be written as
can be written as
The spectral decomposition of ![]() is given by
is given by
![]() .
Suppose that only the first
.
Suppose that only the first ![]() eigenvalues are
positive, i.e.,
eigenvalues are
positive, i.e.,
![]() . Then
the (singular) covariance matrix can be written as
. Then
the (singular) covariance matrix can be written as
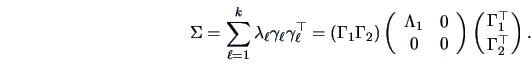

Note that the covariance matrix of model (10.2) can be written as
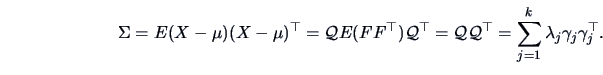 |
(10.3) |
It is common praxis in factor analysis to split the
influences of the factors into common and specific ones.
There are, for example, highly informative factors
that are common to all of the components of ![]() and factors that
are specific to certain components.
The factor analysis model used in praxis is a generalization of (10.2):
and factors that
are specific to certain components.
The factor analysis model used in praxis is a generalization of (10.2):
Define
The generalized factor model (10.4) together with the assumptions given in (10.5) constitute the orthogonal factor model.
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Note that (10.4) implies for the components of
![]() that
that
Assume that a factor model with ![]() factors was found to be
reasonable, i.e., most of the (co)variations of the
factors was found to be
reasonable, i.e., most of the (co)variations of the ![]() measures in
measures in ![]() were explained by the
were explained by the ![]() fixed latent factors. The next natural step
is to try to understand what these factors represent.
To interpret
fixed latent factors. The next natural step
is to try to understand what these factors represent.
To interpret ![]() , it makes sense to compute its correlations
with the original variables
, it makes sense to compute its correlations
with the original variables ![]() first.
This is done for
first.
This is done for
![]() and for
and for
![]() to obtain the matrix
to obtain the matrix ![]() .
The sequence of calculations used here are in fact the same
that were used to interprete the PCs in the principal components analysis.
.
The sequence of calculations used here are in fact the same
that were used to interprete the PCs in the principal components analysis.
The following covariance between ![]() and
and ![]() is obtained via (10.5),
is obtained via (10.5),
Returning to the psychology example where ![]() are the observed scores to
are the observed scores to ![]() different intelligence tests
(the WAIS data set in Table B.12 provides an example),
we would
expect a model with one factor to produce a factor that is positively
correlated with all of the components in
different intelligence tests
(the WAIS data set in Table B.12 provides an example),
we would
expect a model with one factor to produce a factor that is positively
correlated with all of the components in ![]() .
For this example the factor
represents the overall level of intelligence of an individual.
A model with two factors could produce a refinement in explaining the
variations of the
.
For this example the factor
represents the overall level of intelligence of an individual.
A model with two factors could produce a refinement in explaining the
variations of the ![]() scores.
For example, the first factor could be
the same as before (overall level of intelligence),
whereas the second factor could be
positively correlated with some of the tests,
scores.
For example, the first factor could be
the same as before (overall level of intelligence),
whereas the second factor could be
positively correlated with some of the tests, ![]() , that are related to the
individual's ability to think abstractly
and negatively correlated with other tests,
, that are related to the
individual's ability to think abstractly
and negatively correlated with other tests, ![]() , that are related to
the individual's practical ability. The second factor would
then concern a particular dimension of the intelligence stressing the
distinctions between the
``theoretical'' and ``practical'' abilities of the individual.
If the model is true, most of the information coming from the
, that are related to
the individual's practical ability. The second factor would
then concern a particular dimension of the intelligence stressing the
distinctions between the
``theoretical'' and ``practical'' abilities of the individual.
If the model is true, most of the information coming from the ![]() scores
can be summarized by these two latent factors.
Other practical examples are given below.
scores
can be summarized by these two latent factors.
Other practical examples are given below.
What happens if we change the scale of ![]() to
to ![]() with
with
![]() ?
If the
?
If the ![]() -factor model (10.6) is true for
-factor model (10.6) is true for ![]() with
with
![]() ,
, ![]() , then, since
, then, since

The factor loadings are not unique! Suppose that ![]() is an orthogonal
matrix. Then
is an orthogonal
matrix. Then ![]() in (10.4) can also be written as
in (10.4) can also be written as
This implies that, if a ![]() -factor of
-factor of ![]() with factors
with factors ![]() and loadings
and loadings
![]() is true, then the
is true, then the ![]() -factor model with factors
-factor model with factors
![]() and loadings
and loadings
![]() is also true. In practice, we will take advantage of this non-uniqueness.
Indeed, referring back to Section 2.6 we can conclude
that premultiplying a vector
is also true. In practice, we will take advantage of this non-uniqueness.
Indeed, referring back to Section 2.6 we can conclude
that premultiplying a vector ![]() by an
orthogonal matrix corresponds to a rotation of the system of axis, the
direction of the first new axis being given by the first row of the orthogonal
matrix. It will be shown that choosing an appropriate rotation will
result in a matrix of loadings
by an
orthogonal matrix corresponds to a rotation of the system of axis, the
direction of the first new axis being given by the first row of the orthogonal
matrix. It will be shown that choosing an appropriate rotation will
result in a matrix of loadings
![]() that will be easier to
interpret. We have seen that the loadings provide the correlations
between the factors and the original variables, therefore, it makes sense to
search for rotations that give factors that are
maximally correlated with various groups of variables.
that will be easier to
interpret. We have seen that the loadings provide the correlations
between the factors and the original variables, therefore, it makes sense to
search for rotations that give factors that are
maximally correlated with various groups of variables.
From a numerical point of view, the non-uniqueness is a drawback. We
have to find loadings ![]() and specific variances
and specific variances ![]() satisfying the decomposition
satisfying the decomposition
![]() ,
but no straightforward numerical algorithm can solve this problem due to
the multiplicity of the
solutions. An acceptable technique is to impose some
chosen constraints in order to get--in the best
case--an unique solution to the decomposition.
Then, as suggested above, once we
have a solution we will take advantage of the rotations
in order to obtain a solution that is
easier to interprete.
,
but no straightforward numerical algorithm can solve this problem due to
the multiplicity of the
solutions. An acceptable technique is to impose some
chosen constraints in order to get--in the best
case--an unique solution to the decomposition.
Then, as suggested above, once we
have a solution we will take advantage of the rotations
in order to obtain a solution that is
easier to interprete.
An obvious question is: what kind of constraints should we impose in order to
eliminate the non-uniqueness problem? Usually, we impose additional
constraints where
How many parameters does the model (10.7) have without constraints?
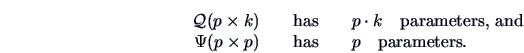
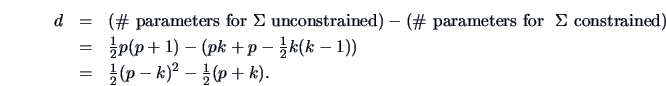
If ![]() , then the model is undetermined: there are infinitly many
solutions to (10.7). This means that the number
of parameters of the factorial model is larger than the number
of parameters of the original model, or that the number of factors
, then the model is undetermined: there are infinitly many
solutions to (10.7). This means that the number
of parameters of the factorial model is larger than the number
of parameters of the original model, or that the number of factors ![]() is ``too large'' relative to
is ``too large'' relative to ![]() . In some cases
. In some cases ![]() : there is an
unique solution to the problem (except for rotation). In practice
we usually have that
: there is an
unique solution to the problem (except for rotation). In practice
we usually have that ![]() :there are more equations than parameters, thus
an exact solution does not exist. In this case
approximate solutions are used.
An approximation of
:there are more equations than parameters, thus
an exact solution does not exist. In this case
approximate solutions are used.
An approximation of ![]() , for example, is
, for example, is
![]() .
The last case is the most interesting
since the factorial model has less parameters
than the original one. Estimation methods are introduced in the next section.
.
The last case is the most interesting
since the factorial model has less parameters
than the original one. Estimation methods are introduced in the next section.
Evaluating the degrees of freedom, ![]() , is particularly important,
because it already
gives an idea of the upper bound on the number of factors we can hope to
identify in a factor model. For instance, if
, is particularly important,
because it already
gives an idea of the upper bound on the number of factors we can hope to
identify in a factor model. For instance, if ![]() , we could not identify a
factor model with 2 factors
(this results in
, we could not identify a
factor model with 2 factors
(this results in ![]() which has infinitly many solutions). With
which has infinitly many solutions). With
![]() , only a one factor model gives an approximate solution (
, only a one factor model gives an approximate solution (![]() ). When
). When
![]() , models with 1 and 2 factors provide approximate solutions and a model
with 3 factors results in an unique solution (up to the rotations) since
, models with 1 and 2 factors provide approximate solutions and a model
with 3 factors results in an unique solution (up to the rotations) since ![]() .
A model with 4 or more factors would not be allowed, but of course, the aim of
factor analysis is to find suitable models with a small number of factors,
i.e., smaller than
.
A model with 4 or more factors would not be allowed, but of course, the aim of
factor analysis is to find suitable models with a small number of factors,
i.e., smaller than ![]() . The next two examples give
more insights into the notion of degrees of freedom.
. The next two examples give
more insights into the notion of degrees of freedom.
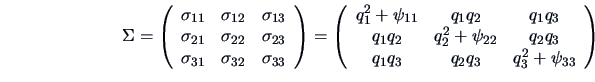
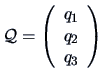 and
and
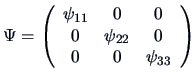 .
Note that here the constraint (10.8) is automatically verified
since
.
Note that here the constraint (10.8) is automatically verified
since 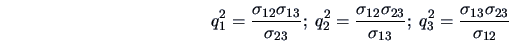
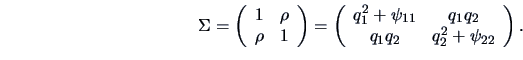
The solution in Example 10.1
may be unique (up to a rotation), but it is not proper in the sense that
it cannot be interpreted statistically.
Exercise 10.5 gives an example where the specific
variance ![]() is negative.
is negative.
1mm
![]()
Even in the case of a unique solution ![]() , the solution may be
inconsistent with statistical interpretations.
, the solution may be
inconsistent with statistical interpretations.