In 1973, the Chicago Board of Options Exchange begun trading options in exchanges, although previously options had been regularly traded by financial institutions in over the counter markets. In the same year, Black and Scholes (1973), and Merton (1973), published their seminal papers on the theory of option pricing. Since then the growth of the field of derivative securities has been phenomenal. In recognition of their pioneering and fundamental contribution to option valuation, Scholes and Merton received in 1997 the Award of the Nobel Prize in Economics. Unfortunately, Black was unable to receive the award since he had already passed away.
In essence, the Black-Scholes model states that by continuously
adjusting the proportions of stocks and options in a portfolio,
the investor can create a riskless hedge portfolio, where all
market risks are eliminated. The ability to construct such a
portfolio relies on the assumptions of continuous trading and
continuous sample paths of the asset price. In an efficient market
with no riskless arbitrage opportunities, any portfolio with a
zero market risk must have an expected rate of return equal to the
risk-free interest rate. This approach led to the differential
equation, known in physics as the "heat equation". Its solution is
the Black-Scholes formula for pricing
European options on non-dividend paying stocks: ![]()
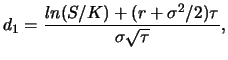
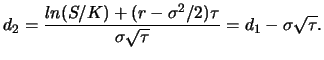
The option price according to the Black-Scholes formula can be calculated with XploRe . First, the functions in library finance must be loaded by typing the command:
library("finance")
There are mainly two ways for computing the option prices according to (11.10) and (11.11) in XploRe. One way is by giving the requested input parameters through interactive menus and the other way is by directly defining the values of the input parameters within the quantlet.
|
 BlackScholes
only calculates the European option price for
a non-dividend paying underlying asset, whereas
BlackScholes
only calculates the European option price for
a non-dividend paying underlying asset, whereas
 bs1
calculates the European option price for different kinds of
dividends and is therefore more general. The input parameter of
the interactive form of
bs1
calculates the European option price for different kinds of
dividends and is therefore more general. The input parameter of
the interactive form of
 bs1
has a value of 1. This means
that the underlying asset pays no dividends. Other values of this
input parameter, in the case of dividend paying underlying asset,
are explained in detail in "Software Application" in subsection
11.2.3. When the direct specification of the input
parameters is selected,
bs1
has a value of 1. This means
that the underlying asset pays no dividends. Other values of this
input parameter, in the case of dividend paying underlying asset,
are explained in detail in "Software Application" in subsection
11.2.3. When the direct specification of the input
parameters is selected,
bs1(S,K,r,sigma,tau,opt,1), the first five follow the usual notation:
 BlackScholes
is used and
BlackScholes
is used and
 bs1
is used. The other two output variables
bs1
is used. The other two output variables For example, the command
BlackScholes(100,120,0.05,0.25,0.5,1)yields the call price of
BlackScholes(100,120,0.05,0.25,0.5,0)yields the put price of
In the following, the basic assumptions and methodology originally employed to derive the option bs1-paprice will briefly be described. The Black-Scholes assumes the following:
| (11.13) |
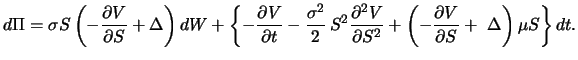
Kwock (1998, pp. 52) provides a probabilistic
interpretation of the option pricing formulae. For example, under
the assumption of risk-neutrality the call option price formula
(11.10), ![]() is seen as the probability of the call
option being in-the-money at expiration. Hence,
is seen as the probability of the call
option being in-the-money at expiration. Hence,
![]() is
the risk neutral expectation of the payment made by the holder of
the call option at expiration by exercising the option. On the
other hand,
is
the risk neutral expectation of the payment made by the holder of
the call option at expiration by exercising the option. On the
other hand,
![]() is the risk neutral expectation
of the asset price at expiration, conditional on the call being
in-the-money. It follows that the expectation of the call value at
expiration is
is the risk neutral expectation
of the asset price at expiration, conditional on the call being
in-the-money. It follows that the expectation of the call value at
expiration is
![]() . This is (in
the risk neutral world) discounted by the factor
. This is (in
the risk neutral world) discounted by the factor
![]() in
order to obtain the present value of the call price.
in
order to obtain the present value of the call price.
The dividend received by holding an asset may be stochastic or
deterministic. The modelling of stochastic dividends is
complicated, since there is another random variable in addition to
the underlying asset. The Black-Scholes formula, however, requires
only some slight modification to remain valid under the crucial
assumption that the dividend yields are deterministic. This means
that over the remaining time to expiration, the option dividends
are at most a known function of time and/or of the underlying
asset. This assumption is not unrealistic given the short-term
life of trade options (generally less than one year) and given the
stable dividend policy that most companies tend to follow over a
short horizon. The prices of European call and put options on
continuously dividend paying underlying asset, noted as ![]() , are:
, are:
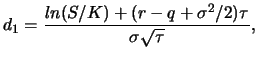
The Black-Scholes pricing formulae show that a European option, on
an underlying asset ![]() paying continuous dividend yields at rate
paying continuous dividend yields at rate
![]() , has the same value as the corresponding European option on an
underlying asset with the price
, has the same value as the corresponding European option on an
underlying asset with the price
![]() that pays no
dividend.
that pays no
dividend.
The quantlets
 bs1
,
bs1
,
 european
and
european
and
 optstart
in
XploRe
can be used to price European options within the
Black-Scholes framework, when dividends exist according to
(11.19) and (11.20) either directly or through
interactive menus.
optstart
in
XploRe
can be used to price European options within the
Black-Scholes framework, when dividends exist according to
(11.19) and (11.20) either directly or through
interactive menus.
|
 european
calculates either the option price by using the
quantlet
european
calculates either the option price by using the
quantlet
 bs1
, or the implied volatility by using the
quantlet
bs1
, or the implied volatility by using the
quantlet
 volatility
. The quantlet
volatility
. The quantlet
 optstart
uses
several interactive menus to compute either i) the price of an
American option through the McMillan formula (subsection
11.2.3) or through binomial trees (subsection
11.3.1), or ii) the price of a European option using the the
Black-Scholes formula, or iii) the implied volatilities (section
11.5).
optstart
uses
several interactive menus to compute either i) the price of an
American option through the McMillan formula (subsection
11.2.3) or through binomial trees (subsection
11.3.1), or ii) the price of a European option using the the
Black-Scholes formula, or iii) the implied volatilities (section
11.5).
The input parameter
![]() in
in
 bs1
is an integer
that specifies the type of the dividend payment: for
bs1
is an integer
that specifies the type of the dividend payment: for
![]() no dividend, for
no dividend, for
![]() continuous
dividends and for
continuous
dividends and for
![]() a fixed dividend at the end
of T is assumed. Finally, if
a fixed dividend at the end
of T is assumed. Finally, if
![]() , then an exchange
rate is assumed as underlying. The call and put formulae for the
foreign currency options are analog to (11.19) and
(11.20), except that the dividend yield
, then an exchange
rate is assumed as underlying. The call and put formulae for the
foreign currency options are analog to (11.19) and
(11.20), except that the dividend yield ![]() is replaced by
the foreign interest rate. In this case,
is replaced by
the foreign interest rate. In this case, ![]() is replaced by the
exchange rate - the domestic currency price of a unit foreign
currency - that is assumed to follow the lognormal diffusion
process. In addition, both domestic and foreign interest rates are
assumed to be constant. In
is replaced by the
exchange rate - the domestic currency price of a unit foreign
currency - that is assumed to follow the lognormal diffusion
process. In addition, both domestic and foreign interest rates are
assumed to be constant. In
bs1(S,K,r,sigma,tau,opt,typeofdiv,div), the first five parameters follow the usual notation. The parameter
When the quantlet ![]() is used interactively,
the output variable
is used interactively,
the output variable ![]() is a scalar containing the computed
option price. The option type is denoted through a (2x1)
dimensional vector
is a scalar containing the computed
option price. The option type is denoted through a (2x1)
dimensional vector ![]() :
: ![]() =
=![]() for a European
call and
for a European
call and ![]() =
=![]() for a European put. The third variable
for a European put. The third variable
![]() is a (6x1) dimensional vector that contains six
input parameters: the price of the underlying asset, the strike
price, the time to expiration, the volatility of the underlying
asset, the domestic risk-free interest rate and the dividend
payment(s).
is a (6x1) dimensional vector that contains six
input parameters: the price of the underlying asset, the strike
price, the time to expiration, the volatility of the underlying
asset, the domestic risk-free interest rate and the dividend
payment(s).
bs1(S,K,r,sigma,tau,opt,typeofdiv,div)offers the possibility to compute simultaneously the price of more than one European call or put option, with or without dividends. The output variable
In order to use (11.19) and (11.20), the quantlet
 bs1
converts the fixed dividend
bs1
converts the fixed dividend ![]() to a constant
continuous dividend yield
to a constant
continuous dividend yield ![]() through
through
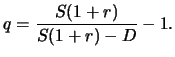
A simple example in which the underlying asset pays continuous
dividend, i.e.
![]() , is given as in the following
, is given as in the following
(230,210,5,25,0.5)for
(S, K, r, \sigma, \tau)and with
(230,210,5,25,0.5)for
(S, K, r, \sigma, \tau), by typing the following commands:
Starting from the left, each column contains for each option the underlying price, the strike price, the continuous risk-free interest rate, the volatility, the time to expiration, the option type, the type of dividend, the dividend payment and the computed option price.
The concept of pricing European options on dividend paying underlying assets will now be briefly outlined.
The constant continuous dividend yield is represented by
![]() . In other words, it is the dividend payment per unit of
time, which always represents the same fraction
. In other words, it is the dividend payment per unit of
time, which always represents the same fraction ![]() of the stock
price. The holder then receives dividend payment(s) equal to
of the stock
price. The holder then receives dividend payment(s) equal to
![]() within the interval
within the interval ![]() . As the price of the underlying
asset falls by the amount of the dividend, the asset price
dynamics based on the geometric Brownian motion model becomes
. As the price of the underlying
asset falls by the amount of the dividend, the asset price
dynamics based on the geometric Brownian motion model becomes
For every asset held ![]() is received. The holder of the
portfolio, who holds
is received. The holder of the
portfolio, who holds ![]() assets, earns an amount equal to
assets, earns an amount equal to
![]() and dividend payment(s) equal to
and dividend payment(s) equal to
![]() in the
interval
in the
interval ![]() . The change in value of the portfolio
. The change in value of the portfolio ![]() is given
by
is given
by
where
![]() . The last term
. The last term
![]() denotes the wealth added to the portfolio due to the
dividend yields. By applying the no arbitrage argument, the hedged
portfolio should earn the risk-free interest rate, so that
denotes the wealth added to the portfolio due to the
dividend yields. By applying the no arbitrage argument, the hedged
portfolio should earn the risk-free interest rate, so that
This leads to the following modified form of the Black-Scholes equation:
For a call option, the only change to the boundary conditions is
The final condition is still
![]() . Without working
through a similar integration procedure, the price of a European
option can be obtained by a simple modification of the
Black-Scholes price formula. The European option on an underlying
asset with price
. Without working
through a similar integration procedure, the price of a European
option can be obtained by a simple modification of the
Black-Scholes price formula. The European option on an underlying
asset with price ![]() paying continuous dividend yields at rate
paying continuous dividend yields at rate ![]() has the same value as the corresponding European option on an
underlying asset with the price
has the same value as the corresponding European option on an
underlying asset with the price
![]() that pays no
dividend. This yields the option valuation formulae
(11.19) and (11.20).
that pays no
dividend. This yields the option valuation formulae
(11.19) and (11.20).
Note, that if the underlying asset is a commodity, like grain or
livestock, there may be additional costs in holding the asset,
such as storage or insurance. In simple terms, these additional
costs, denoted for example with ![]() , can be considered as
negative dividends paid by the underlying asset. In this case, the
option price is equivalent to (11.19) and (11.20),
where the continuous compound dividend
, can be considered as
negative dividends paid by the underlying asset. In this case, the
option price is equivalent to (11.19) and (11.20),
where the continuous compound dividend ![]() is simply replaced
by
is simply replaced
by ![]() . The term
. The term ![]() is interpreted as the cost of carry,
denoted with
is interpreted as the cost of carry,
denoted with ![]() . It consists of two parts, the costs of funds
tied up in the asset that require interest for borrowing and
additional costs due to storage, insurance etc. When the
underlying asset pays a continuous dividend
. It consists of two parts, the costs of funds
tied up in the asset that require interest for borrowing and
additional costs due to storage, insurance etc. When the
underlying asset pays a continuous dividend ![]() , then the cost of
carry
, then the cost of
carry ![]() equals
equals ![]() , and the Black-Scholes differential
equation (11.17) is written as
, and the Black-Scholes differential
equation (11.17) is written as
An American option confers all the rights of its
European counterpart plus the privilege of early exercise. Since
this additional privilege should not be worthless, it has
potentially a higher value than its European counterpart. The
extra cost is usually called early exercise premium. An
exception to this is an American call option on non-dividend
paying underlying asset, whose price always equals its European
counterpart. For other American options it may be optimal to
exercise them prior to expiration. For an American call or put,
this only happens when the price of the underlying asset at a
given time to expiration ![]() , rises above (falls below) a
critical asset value
, rises above (falls below) a
critical asset value ![]() , known as the optimal
exercise price. The collection of these critical values for all
times constitutes a curve, which is known as the optimal
exercise boundary. It is not a known priori where to apply the
boundary condition, so that the optimal exercise boundary has to
be determined in the solution process.
, known as the optimal
exercise price. The collection of these critical values for all
times constitutes a curve, which is known as the optimal
exercise boundary. It is not a known priori where to apply the
boundary condition, so that the optimal exercise boundary has to
be determined in the solution process.
The early exercise premium can be expressed in terms of the exercise boundary in a stochastic integral. A detailed explanation is given in Kwock (1998, ch. 4) and Wilmott et al. (1997, ch. 7). The direct solution of the stochastic integral equation is in many cases unmanageable, so that several analytic approximation methods for the valuation of American options and the associated optimal exercise boundaries have been developed.
In
 XploRe
the price of the American option is computed by
using the popular quadratic approximation method, which was first
proposed by MacMillan (1986) for non-dividend paying stock
options and later extended to commodity options by
Barone-Adessi and Whaley (1987). This class of approximation methods
involves the reduction of the Black-Scholes partial differential
equation to an ordinary one. The idea is to transform the
Black-Scholes differential equation (11.17), so that the
temporal derivative term can be considered as a quadratic small
term and then dropped as an approximation (Kwock; 1998, pp. 166).
Then applying the boundary conditions, the prices of American call
and put options follow.
XploRe
the price of the American option is computed by
using the popular quadratic approximation method, which was first
proposed by MacMillan (1986) for non-dividend paying stock
options and later extended to commodity options by
Barone-Adessi and Whaley (1987). This class of approximation methods
involves the reduction of the Black-Scholes partial differential
equation to an ordinary one. The idea is to transform the
Black-Scholes differential equation (11.17), so that the
temporal derivative term can be considered as a quadratic small
term and then dropped as an approximation (Kwock; 1998, pp. 166).
Then applying the boundary conditions, the prices of American call
and put options follow.
The price of an American call for ![]() equals the price of its
European counterpart (see subsection 11.2.4 for an example). The price of an American call for
equals the price of its
European counterpart (see subsection 11.2.4 for an example). The price of an American call for ![]() is:
is:
The price of an American put option is given in (11.27)
and holds for all values of ![]() .
.
![]() and
and ![]() are estimated by solving the following
equations (11.28) and (11.29) iteratively
are estimated by solving the following
equations (11.28) and (11.29) iteratively
The other variables used in (11.28) and (11.29) are
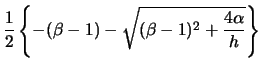 |
(11.30) | ||
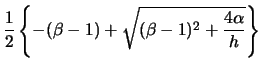 |
(11.31) | ||
![$\displaystyle -\frac{S^{**}}{\gamma_1}\left[1-exp{\left\{(b-r)\tau\right\}}\;\Phi\left\{-d_1(S^{**})\right\}\right]$](xlghtmlimg1044.gif) |
(11.32) | ||
![$\displaystyle \frac{S^{*}}{\gamma_2}\left[1-exp{\left\{(b-r)\tau\right\}}\;\Phi\left\{d_1(S^{*})\right\}\right]$](xlghtmlimg1046.gif) |
(11.33) | ||
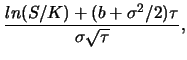 |
(11.34) |
XploRe offers the following quantlets to calculate the price of american options using the MacMillan approximation:
|
The price of American options can be calculated directly with the
quantlet
 mcmillan
or through interactive menus by using
mcmillan
or through interactive menus by using
 american
. The third quantlet
american
. The third quantlet
 optstart
is more
general. It uses several interactive menus to compute the price of
American or European options, or their implied volatility.
However, in spite of the different comfortability that quantlet
optstart
is more
general. It uses several interactive menus to compute the price of
American or European options, or their implied volatility.
However, in spite of the different comfortability that quantlet
 american
or
american
or
 optstart
offers, both use the quantlet
optstart
offers, both use the quantlet
 mcmillan
to calculate the price of American options.
mcmillan
to calculate the price of American options.
The parameter
![]() specifies the price of the European
option. The option type is specified through the (2x1) dimensional
vector
specifies the price of the European
option. The option type is specified through the (2x1) dimensional
vector ![]() , with
, with ![]() =
=![]() for American call and
for American call and
![]() =
=![]() for put. The third variable
for put. The third variable
![]() is a
(6x1) dimensional vector that contains six input parameters: the
price of the underlying asset, the strike price, the time to
expiration, the annualized volatility of the underlying asset, the
annualized risk-free interest rate and the dividend payment(s).
The following example computes the price of an American option on
non-dividend paying underlying asset.
is a
(6x1) dimensional vector that contains six input parameters: the
price of the underlying asset, the strike price, the time to
expiration, the annualized volatility of the underlying asset, the
annualized risk-free interest rate and the dividend payment(s).
The following example computes the price of an American option on
non-dividend paying underlying asset.
The
XploRe
output shows the expected result, that an American
call on a non-dividend paying underlying asset will have the same
price as its European counterpart:
A second example computes the price of an American option when
the underlying is a commodity that involves continuous annualized
costs of around 5% of the commodity. The annualized risk-free
interest rate is ![]() , so that the cost of carry is
, so that the cost of carry is
![]() .
.
When ![]() the value of the American call is given in
(11.26). It is always higher than the price of its European
counterpart, as illustrated in a third example.
the value of the American call is given in
(11.26). It is always higher than the price of its European
counterpart, as illustrated in a third example.
 Xplore
output is:
Xplore
output is:
The quadratic approximation method will be briefly outlined
following Hull (2000, pp. 432-434) and Kwock (1998, pp.
174-177). Consider an American option on a stock, paying
continuous dividends at rate
![]() . The early exercise premium, defined by
. The early exercise premium, defined by ![]() , is
, is
and defining
equation (11.35) can be transformed into the following form