11.5 Implied Volatility

The volatility of an asset is a measure of variability of its returns. Traditionally, volatility is measured on past prices of the underlying asset, known as historical volatility. However for investors, who have a high regard for the 'wisdom' of the market, the best estimate of volatility comes from the market itself.

If the market price of the option is taken to be the correct price, then the volatility implied by the market price reflects the market's opinion of what the volatility should be. The value of the volatility of the underlying asset that would equate the option price to its fair value, is called implied volatility. In other words, implied volatility is the volatility, which is implicitly contained in the option price (Alexander; 1996, pp. 14). It is a timely measure - it reflects the market's perceptions today - and it should therefore provide the market's best estimate of future volatility (Jorion; 2001). This is therefore one reason to believe that option-based forecasts can be superior to historical estimates. Supporting evidence on this point is for example provided in Jorion (1995) and Campa and Chang (1998).

Implied volatilities are a useful tool in monitoring the market's opinion regarding the volatility of a particular stock. Besides this, options are often traded on volatility with the implied volatility becoming the effective price of the option. Implied volatility also has important implications for risk management. If volatility increases, so will the value at risk (VaR). Investors may want to adjust their portfolio in order to reduce their exposure to those instruments, whose volatility is predicted to increase. Hence, in a delta hedged portfolio the vega risk (see subsection 11.4.4) can become the most significant risk factor within the portfolio.

When an explicit analytic option pricing formula is available, as for instance the Black-Scholes formula (11.10), the quoted price of the option along with known variables, such as the price of the underlying asset $\tt {S}$, the exercise price $\tt {K}$, time to expiration $\tt {tau}$ and the interest rate $\tt {r}$ can be used in an implicit formula to calculate the so called implied volatility. The Black-Scholes implied volatility refers to the market price of the option equal to the price given by the Black-Scholes formula (11.10). For a call option, it can be written as

$$C(S_t,K,\tau,r,\sigma_I(K,\tau))=C^*_t(K,\tau),$$ (11.64)

where $C(S_t,K,\tau,r,\sigma_I(K,\tau))$ is the Black-Scholes call price, $\sigma_I(K,\tau)$ is the implied volatility and $C^*_t(K,\tau)$ is the market price of the call at time instant $\tt {t}$. The implied volatility of a European put with the same strike and maturity can be derived from the put-call parity (11.18). The existence of the uniqueness of the implied volatility in (11.64), is due to the fact that the value of a call option as a function of volatility is a monotonic mapping from $[0,\infty[$ to $]0,\;S_t-Kexp{(-r\tau)}[$.

The Black-Scholes model assumes that the underlying asset follows a Brownian motion with constant volatility. If this model is correct, then the distribution of the underlying asset at any option expiration is lognormal, and all options on the underlying asset must have the same implied volatility. Since the market crash in 1987, the market implied volatilities for index options have shown that at-the-money options yield lower volatilities than in-the-money or out-of-the-money options. The convex shape of the implied volatility with respect to the moneyness ($K/S$) is referred to as the smile effect. The smile effect occurs as at-the-money options are more sensitive to volatility, so that a smaller volatility spread is required for them to achieve the same profit or risk premium as out-of-the-money options.

Jarrow and Rudd (1982) argued that this smile effect can be partially explained by departures from lognormality in the underlying asset price, particulary for out-of-the-money options. The smile is particularly noticeable in the Black-Scholes implied volatility - possibly because of the inappropriate assumptions underlying the Black-Scholes model - and tends to increase as the option approaches expiration (Hull and White; 1987). Hence, the value of the implied volatility depends on time to expiration $\tau$ and strike $\tt {K}$. The function

$$\sigma_I: \hspace{0.5cm}(K,\tau)\longrightarrow\sigma_I(K,\tau)$$ (11.65)

is called the implied volatility surface at date $\tt {t}$, i.e. it is the plot of implied volatility across strike and time to maturity. Using the moneyness of the option, $m=K/{S_t}$, the implied volatility surface can be represented as a function of moneyness and of time to expiration. This graphical representation is convenient, because there is usually a range for moneyness around $m=1$, where options are liquid and therefore empirical data is available (Cont and da Fonseca; 2002). The quantlet volsurf in XploRe offers the choice to plot the implied volatiliy surface either as a function of $(K,\tau)$ or of $(m,\tau)$.

The dependence of implied volatility on strike and maturity is analyzed by various authors for different markets. It is empirically found that the implied volatility surface exhibits a non-flat profile with respect to both strike and term structure, which contradicts the flat profile provided by the Black-Scholes model. Evidence of this is given for example in Dumas et al. (1996), Fengler et al. (2001), Franks and Schwarz (1991), Heynen (1993), Hodges (1996), and Rebonato (1999). The dynamic properties of the implied volatility time series is mainly analyzed using the Principal Component Analysis (PCA). In this context, a cross-section of the implied volatility surface in one direction is considered. If the cross-section is made on different points of the moneyness axis, then a series of term structure-curves is obtained. Analogously, if this is done on the time to expiration axis, a series of smile-curves is obtained. Then the PCA is applied. Examples of the term structure of at-the-money implied volatilities using the PCA can be found in Härdle and Schmidt (2000), Heynen et al. (1995), Zhu and Avellaneda (1997).

There are however some shortcomings with implied volatilities. There is considerable evidence that these volatilities are themselves stochastic. Typically the shape of the distribution (and hence the smile) is unstable because of 'volatility of volatility'. Another problem is that the asset returns and volatility may be correlated, but often non-linearly, usually reflected in fat-tailed and skewed distributions of the underlying asset. Implied volatilities can also be biased, especially if they are based upon options that are thinly traded.

11.5.1 Software Application

XploRe offers different algorithms to calculate implied volatilities. Further on, the volatility surfaces can be constructed through parametric or non-parametric approaches and plotted. Fengler et al. (2001) analyze implied volatilities using XploRe as a computational tool, see e-book
Applied Quantitative Finance, ch. 7.

11.5.1.1 Computing Implied Volatility

In practice several implied volatilities are obtained simultaneously from different options on the same stock and a composite implied volatility for the stock is then calculated by taking a suitably weighted average of the individual implied volatilities. Note, that XploRe computes only the implied volatilities from each option. If a composite implied volatility is required, the user then has to decide about the weighting scheme. It is however important that the weights reflect the sensitivity of the option prices to volatility, such as the price of the at-the-money option is far more sensitive to volatility than the price of the deep out-of-the-money option. Different weighting schemes are discussed in Latene and Rendelman (1976), by Chiras and Manaster (1978), and in Whaley (1982).

european ()

calculates the prices of European options, or their implied volatilities, specifying interactively the input parameters.

ImplVola (x,IVmethod)

calculates implied volatilities assuming the Black-Scholes model for European options by using either the Newton-Raphson or bisections method. The input parameters are specified either interactively or directly.

volatility (task)

volatility (S,K,r,tau,opt,optprice,tyoeofdiv,div)

calculates implied volatilities of European options, specifying either interactively or directly the input parameters.

european uses the quantlet volatility to compute implied volatilites. Note, that the quantlet optstart is not explicitly mentioned as it performs no calculation. It calls either the quantlet european , or american to compute implied volatilities for european and american options respectively. XploRe does not recommend the calculation of implied volatilities for American options valuated with the MacMillan approximation method (see subsection 11.2.4).

ImplVola offers two different algorithms to calculate implied volatilities, the bisection and the Newton-Raphson. The most widely used technique for the estimation of the implied volatility is the Newton-Raphson iterative algorithm. It involves making an initial guess as to the implied volatility of the option. It then uses the Greek derivative of the option price relative to changes in volatility (the vega) to make a new guess if the initial guess is off the mark. Tompkinks (1994, pp. 143) writes the algorithm as the following:

$$\sigma_{i+1} = \sigma_i-\frac{Y_i-P}{\Lambda_i}$$

$$until ~ \hspace{0.5cm} \mid Y_i-P\mid \leq\epsilon$$

where

$$P = \textrm{traded option price,}$$

$$\sigma_i = \textrm{volatility estimate,}$$

$$Y_i = \textrm{option theoretical value with $\sigma_i$\ volatility,}$$

$$\Lambda_i = \textrm{options vega at theoretical price $Y_i$,}$$

$$\epsilon = \textrm{desired degree of accuracy.}$$

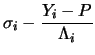The convergence to the correct answer is often achieved in only two or three iterations, if the option price relationship to time is continuous and relatively linear. This is the case for European vanilla options, where the price-volatility relationship is a smooth, relatively linear curve. For other kinds of options including American options, where a significant probability of early exercise exists, or for complex options, which have a kinked rather than a smooth price-volatility relationship, this technique may not work. For these types of options, the bisection method is then preferred. The bisection algorithm can be described as the following:

Step 1. Pick $\sigma_0$ and $\sigma_1$ so that

$$\sigma_0<\sigma \hspace{1cm} \textrm{i.e.} \hspace{0.4cm}C(\sigma_0)<C_{observed}$$

$$\sigma_1>\sigma\hspace{1cm} \textrm{i.e.} \hspace{0.4cm}C(\sigma_1)>C_{observed}$$

Step 2. Choose $\sigma_2=\frac{\sigma_0+\sigma_1}{2}$

If $C(\sigma_2)>C_{observed}$ then $\sigma_3=\frac{\sigma_0+\sigma_2}{2}$, else $\sigma_3=\frac{\sigma_1+\sigma_2}{2}$

Step 2 is repeated until a sufficiently good approximation for $\sigma$ is obtained.

In the following example ImplVola is used to calculate implied volatilities for four different options (two calls and two puts) on different underlying assets with the Newton-Raphson algorithm:

library ("finance")
 assetprice = #(5290.36,5290.36,5290.36,5290.36); input data - S
 strike = #(5350,5500,3700,3800)                ; input data - K
 irate = #(0.03294,0.03294,0.03294,0.03294)     ; input data - r
 maturity = #(0.13425,0.13425,0.13425,0.13425)  ; input data - tau
 optionprice = #(221.6,154.2,4.9,6.4)        ; input data - C
 type = #(1,1,0,0)                           ; 2 calls, 2 puts
 x=assetprice~strike~irate~maturity~optionprice~type ; data matrix
 ivola=ImplVola(x)                           ; compute ImplVola
 ivola                                       ; display ImplVola

XLGfindex12.xpl

The XploRe output shows the calculated implied volatilities:

Contents of ivola

 [1,]  0.30842
 [2,]  0.2993
 [3,]  0.47033
 [4,]  0.45812

Implied volatility for the first European call option is $\tt {0.30842}$. For the same option, implied volatility is $\tt {0.3087}$ when calculated with the quantlet volatility . The examples show that it makes no significant difference if implied volatility is computed using ImplVola or volatility . The results differ only by $10^{-4}$.

volatility computes the implied volatility of each european option as a result of an optimization process of the option price along the volatility $\sigma$. It uses the function nelmin , which searches for a minimum of the squared option price function. In each iteration step the function is evaluated at a simplex of (p+1) points. The iteration stops when the variance is less than a predetermined value or when a given iteration number is reached. Technical details are given in Nelder and Mead (1965).

The input parameter $\tt {task}$ in volatility is a scalar that specifies the type of the dividend payment: for $\tt {task}=1$ no dividend, for $\tt {task}=2$ a continuously paid dividend and for $\tt {task}=3$ a fixed dividend at the end of T is assumed. Finally, if $\tt {task}=4$, then an exchange rate is assumed as underlying.

The following example calculates the implied volatility for only one European call, when no dividends are assumed:

library("finance")
 volatility(1)             ; no dividends

XLGfindex13.xpl

 
with the input values $\tt {(30, 230, 210, 5, 0.5)}$ for ($C$,$S$, $K$, $r$, $\tau$). Using the quantlet european yields the same result for implied volatility.

The output window yields:

Contents of aus
 [1,] " "
 [2,]"-------------------"
 [3,] " The Implied Volatility of Your Option "
 [4,] " on Given Stock is "
 [5,] "0.2292"
 [6,]"-------------------"
 [7,] " "

It is possible to calculate simultaneously implied volatility for one or more options by specifying input parameters directly in

volatility(S,K,r,tau,opt,optprice,tyoeofdiv,div)

.

11.5.1.2 Construction of Smooth Volatility Surfaces

The usual practice to construct implied volatility surfaces for arbitrary strikes $\tt {K}$ and maturities $\tt {tau}$ is to smooth the discrete data. This can be done in a parametric or non-parametric way. For example, it is common practice in many banks, to use (piecewise) polynomial functions to fit the implied volatility smile (Dumas et al.; 1996). XploRe offers the following two quantlets to construct and plot volatility surfaces:

volsurf (x,stepwidth,firstXF,lastXF,firstMat,lastMat,metric,

bandwidth,p,IVmethod)calculates the implied volatility surface using a Kernel smoothing procedure, specifying directly the input parameters.

volsurfplot (IVsurf,IVpoints,AdjustToSurface)

plots the implied volatility surface computed by the quantlet volsurf with original options shown as red points, specifying directly the input parameters.

volsurf computes the implied volatility surface using a kernel smoothing procedure. Either a Nadaraya-Watson estimator or a local polynomial regression is employed.

The local polynomial method is used to estimate an unknown function $m$, which expresses a functional dependence between an explanatory variable $(X_1,X_2)=(K,\tau)$ and the dependent variable $\sigma(X_1,X_2)=m(X_1,X_2)$ . In contrast to the parametric regression, there are no restrictions on the form of $m(\cdot)$, i.e. theory does not state whether $m(\cdot)$ is linear, quadratic or increasing in $(X_1,X_2)$ (Härdle et al.; 2001). The local polynomial method is based on the idea that under suitable conditions, the function $m$ can be locally, i.e. at an observation point $(x_{10}x_{20})$, approximated through a Taylor expansion. The local polynomial can then be fitted by a weighted least squared regression problem. Only the observations, which are close enough to $(x_{10}x_{20})$ have to be considered in the minimization process. The neighborhood is realized by including kernel weights into this process. In contrast to the parametric least squares, the estimator varies with the observations $(x_{1i},x_{2j})$ for $i,j=0, 1 ...n$. The whole surface is obtained by running the above local polynomial regression for each observation $(x_{1i},x_{2j})$.

Alternatively, volsurf uses the filtered data set to construct a smooth estimator of the implied volatility surface, defined on a fixed grid, using the non-parametric Nadaraya-Watson estimator. Given the exploratory variables $(X_1,X_2)=(K,\tau)$, the two dimensional Nadaraya-Watson kernel estimator is

$$\hat{\sigma}(x_1,x_2)=\frac{\sum^n_{i=1}K_1\left(\frac{x_1-x_{1i}... ...K_1\left(\frac{x_1-x_{1i}}{h_1}\right) K_2\left(\frac{x_2-x_{2i}}{h_2}\right)},$$ (11.66)

where $\hat{\sigma_i}$ is the implied volatility from the observed option price, $K_1$ and $K_2$ are univariate kernel functions, and $h_1$ and $h_2$ are the bandwidths.

volsurf uses a quartic Kernel for both, the local polynomial and the Nadaraya-Watson estimator. The order 2 quartic kernel is given by

$$K_i(u)=\frac{15}{16}(1-u^2)^2I(\vert u\vert\leq 1).$$ (11.67)

The choice of another kernel, for instant a Gaussian kernel as in Cont and da Fonseca (2002), instead of quartic Kernel does not influence the results very much. The important parameters are the bandwidth parameters $h_1$ and $h_2$ which determine the degree of smoothing. Too small values will lead to a bumpy surface, too large ones will smooth away important details. Härdle (1994, ch. 5) and Härdle et al. (2001, ch. 4.3) discuss different ways how to calculate the bandwidth, as for instance using a cross-validation criterion, or an adaptive bandwidth estimator in order to obtain an 'optimal' bandwidth.

The first input parameter $\tt {x}$ in volsurf is a (n x 6) dimensional data matrix. The columns one to six contain: underlying asset prices $\tt {S}$, strike prices $\tt {K}$, interest rates $\tt {r}$, time to expiration $\tt {tau}$, option prices and types of option (1 for call and 0 for put). The next five input parameters are concerned with the construction of the volatility surface. $\tt {stepwidth}$ is a (2 x 1) dimensional vector, where the first element refers to the strike dimension and the second to time to expiration. $\tt {firstXF}$ ( $\tt {lastXF}$) and $\tt {firstMat}$ ( $\tt {lastMat}$) are scalar constants giving the lowest (highest) limit of the strike dimension and of time to expiration in the volatility surface, respectively. The metric in volsurf is either moneyness $K/F$ ( $\tt {metric=0}$), where $F$ is the (implied) forward price of the underlying asset computed as $F_t=S_texp(r\tau)$, or is the original strike price $K$ ( $\tt {metric=1}$). The parameter $\tt {bandwidth}$ is a (2 x 1) dimensional vector determining the width of the bins for the kernel estimator. The parameter $\tt {p}$ is a scalar, which indicates whether the Nadaraya-Watson estimator ($\tt {p=0}$) or the local polynomial regression ( $\tt {p}\neq\tt {0}$) is used. The last parameter, $\tt {IVmethod}$, is optional. As in quantlet ImplVola , if $\tt {IVmethod=''bisect''}$ then the bisection method is used to compute implied volatilities. The default method is the Newton-Raphson algorithm (see subsection 11.5.1).

The output of the quantlet volsurf consists of two variables. The first one, $\tt {IVsurf}$, contains the co-ordinates of the points computed for the volatility surface. It is a (N x 3) dimensional matrix, where N is the number of grid points. The second one, $\tt {IVpoints}$, is a (M x 3) dimensional matrix, which contains the co-ordinates of the M options used to estimate the surface. In both variables, the columns one to three contain the values of strike dimension, of time to expiration and of estimated implied volatility, respectively.

volsurfplot is a graphical tool used to display the volatility surface constructed with the quantlet volsurf . Therefore the input parameters are the co-ordinates of the volatility surface $\tt {IVsurf}$ and of the original option values contained in $\tt {IVpoints}$, which were used in volsurf to construct the surface. The third input parameter $\tt {AdjustToSurface}$ is optional. It determines, whether the graph-limits are based on the original option observations stored in $\tt {IVpoints}$, or based on coordinates of estimated surface $\tt {IVsurf}$. By default $\tt {AdjustToSurface=1}$, the graph is adjusted according to the estimated surface.

To illustrate, two examples as given in the description part of volsurf are used. The first example constructs the volatility surface in moneyness metric ( $\tt {metric=0}$), using the Nadaraya-Watson estimator ( $\tt {p}=\tt {0}$). The implied volatilities are computed with the bisection method
( $\tt {IVmethod=''bisect''}$).

library ("finance")
 data=read("volsurfdata2.dat"); reads data
 IVmethod="bisect"            ; computes implied volatilities
 sw=0.02|(1/52)´               ; stepwidth
 bw=0.1|0.4                   ; bandwidth
 fXF=0.8                      ; firstXF
 lXF=1.2                      ; lastXF
 fMat=0                       ; firstMat
 lMat=1                       ; lastMat
 metric=0                     ; computes in moneyness dimension
 AdjustToSurface=1
 IVSurface,IVpoints=volsurf(data,sw,fXF,lXF,fMat,lMat,metric,
                            bw,0,IVmethod)
 volsurfplot(IVSurface,IVpoints,AdjustToSurface)

XLGfindex14.xpl

volsurfplot displays the implied volatility surface as a function of moneyness and time to expiration in years (Figure 11.22). The original options are marked red. The graph shows a decreasing profile in moneyness ('skew') and changes in the volatility term structure. The 'skew' is the degree of asymmetry on upper and lower sides of the underlying distribution.

$\parbox{13cm}{\caption{\small Implied v... ...lied volatility surface is constructed using \ the Nadaraya-Watson estimator.}}$

A second example constructs the volatility surface also using the default Nadaraya-Watson estimator ($\tt {p=0}$), but in strike metric ( $\tt {metric=1}$), for the same data set as in the previous example. The implied volatilities are now computed with the default Newton-Raphson algorithm.

library ("finance")
 data=read("volsurfdata2.dat") ; reads data
 sw=70|(1/52)´               ; stepwidth
 bw=250|0.5                    ; bandwidth
 fXF=3500                       ; firstXF
 lXF=7000                      ; lastXF
 fMat=0                        ; firstMat
 lMat=1                        ; lastMat
 metric=1                     ; calculates in strike dimension
 AdjustToSurface=1
 IVSurface,IVpoints=volsurf(data,sw,fXF,lXF,fMat,lMat,metric,bw,1)
 volsurfplot(IVSurface,IVpoints,AdjustToSurface)

XLGfindex15.xpl

volsurfplot displays the implied volatility surface as a function of strike price and of time to expiration in years (Figure 11.23). The slight difference between the two surfaces relates to the different algorithms used for computing the implied volatilities. However, the profile in strike is mainly downward sloping and the profile in maturity shows a variable volatility term structure. Both examples confirm the well-known evidence that the implied volatility surface is other than flat, which would be the case if the assumption of constant volatility in the Black-Scholes model was correct.

$\parbox{13cm}{\caption{\small Implied v... ...lied volatility surface is constructed using \ the Nadaraya-Watson estimator.}}$

11.5.2 Implied Binomial Trees

The variation of implied Black-Schloles volatilities, with both strike and expiration is currently a persistent feature of option markets. Jarrow and Rudd (1982) argue that the smile for a given maturity can be partially explained by departures from lognormality in underlying asset prices, particulary for out-of-the-money options. Researchers have attempted to enrich the Black-Scholes model to account for the smile. Extensions, such as jumps in the underling asset price (see subsection 11.1.2) or stochastic volatility factor (Hull and White; 1987), unfortunately cause several practical difficulties, for example the violation of the risk-neutral condition (Härdle and Zheng; 2001).

Implied binomial trees (IBT) proposed by Derman and Kani (1994), Dupire (1994), Rubinstein (1994), Barle and Cakici (1998) account for risk-neutrality and extend the Black-Scholes theory, making it consistent with the shape of the smile. This consistency is achieved by extracting the implied evolution of the stock price from the market prices of liquid European vanilla options on the underlying stock.

CRR is a binomial tree, which is a discrete version of the geometric Brownian motion (11.4). Similarly, IBT and any other multinomial tree can be viewed as discrete versions of the following diffusion process of the underlying asset:

$$\frac{dS_t}{S_t} = \mu_t\, dt + \sigma(S_t,t)\, d W(t)$$ (11.68)

The variable $\mu_t$ is the risk-neutral drift and $\sigma (S_t,t)$ is the instantaneous local volatility function, which is dependent on both underlying price and time. Models of this type usually involve a special parametric form of $\sigma (S_t,t)$. In contrast, the IBT approach deduces $\sigma (S_t,t)$ numerically from the smile. It ensures that local volatility varies from node to node, so that the market price of any plain vanilla option can be matched. Option prices for all strikes and expirations, obtained by interpolation from known option prices, will determine the position and the probability of reaching each node in the implied tree (Derman and Kani; 1994). The standard (CRR) binomial tree Figure (11.4) is then replaced by a distorted or implied tree as in Figure (11.24).

$\parbox{9.5cm}{\caption{\small Implied binomial tree with volatility $\sigma(S_t,t)$}\cite{de:ka:ch:96}}$

The IBT and any other implied tree should satisfy the following conditions:

• the tree correctly reproduces the volatility smile,
• the tree is risk-neutral,
• all transition probabilities are positive and less than one.

The last two conditions will eliminate arbitrage opportunities. The concept of constructing an implied binomial tree, based on the Derman and Kani (1994) algorithm, is explained briefly in subsection (11.5.2). It is also applied in XploRe for constructing implied binomial trees (see subsection 11.5.2). A detailed explanation of implied binomial trees and their construction within XploRe is provided by (Härdle and Zheng; 2001), in e-book
Applied Quantitative Finance, ch.7 .

When constructing an implied binomial tree, (see subsection 11.5.2) there is only one free parameter, which allows an arbitrary choice for the central node at each level of the tree. In a continuous limit, where there are an infinite number of nodes at each time step, this choice becomes irrelevant. Consequently, there is a unique implied binomial tree that fits option prices in any market. This feature can be disadvantageous, because there is no room for adjustment by inconsistency and/or arbitrage, or by implausible local volatility and probability distribution. One possible solution is to make the structure of the implied tree more flexible by using implied trinomial trees (see subsection 11.5.3).

11.5.2.1 Software Application

XploRe offers the possibility to generate the IBT by using either the quantlet IBTdk , which is based on the Derman and Kani (1994) method, or the quantlet IBTbc based on the Barle and Cakici (1998) method:

IBTdk (S,r,lev,expiration,volafunc)

calculates the stock prices on the nodes of the implied tree, the transition probability tree and the tree of Arrow-Debreu prices, using Derman and Kani's method.

IBTbc (S,r,lev,expiration,volafunc)

calculates the stock prices on the nodes of the implied binomial tree, the transition probability tree and the tree of Arrow-Debreu prices, using Barle and Cakici's method.

IBTlocsigma (ptree,prob,m,deltat)

estimates the implied local volatility of each node in the implied binomial tree.

IBTvolaplot (loc,step,startpoint,endpoint,m)

shows the implied local volatility surface sigma(S,tau) in the implied tree at different times to expiration and stock price levels.

In IBTdk and IBTbc , the input parameter $\tt {S}$ stands for the underlying asset price, $\tt {r}$ for the continuously compounded risk-free interest rate, $\tt {lev}$ for the number of time steps and $\tt {expiration}$ for time to expiration. The last parameter $\tt {volafunc}$ is a string, specifying the name of the function used to define how the Black-Scholes implied volatilities change with strike and expiration.

Both quantlets IBTdk and IBTbc output the tree of underlying asset prices, contained in a $(n+1)\times(n+1)$ dimensional matrix, the tree of transition probabilities contained in a $(n\times n)$ dimensional matrix and the tree of Arrow-Debreu prices contained in a $(n+1)\times(n+1)$ dimensional matrix.

The following example illustrates how to generate an IBT using the Derman and Kani method. The Black-Scholes implied volatility is assumed to be a linear function of $(S-K)/S$. The IBT corresponds to $\tau=1$ year and $\Delta t=0.25$ year.

library("finance")
 proc(sigma)=volafunc(K, S, time)
 sigma=0.1+(S-K)/S/10*0.5
 endp
 r=0.03          ; annualized risk-free interest rate
 S=100           ; underlying asset price
 lev=4           ; number of time steps
 expiration=1    ; annualized time to expiration
 ibtree=IBTdk(S,r,lev,expiration,"volafunc")
 ibtree
 

XLGfindex16.xpl

The output shows the one year stock price implied binomial tree ibtree.Tree, the transition probability tree ibtree.prob and the Arrow-Debreu price tree ibtree.lb. The elements at the $n$th column of the ibtree.Tree matrix correspond to the stock prices at the level $(n-1)$ of the tree. The element $(n,i)$ of the $n$th column and $i$th row of the ibtree.prob matrix corresponds to the transition probability of moving from node $(n,i)$ to node $(n+1,i+1)$. Using the Arrow-Debreu prices from the ibtree.lb matrix together with the stock price at respective nodes, a discrete approximation of the implied distribution of the stock prices can be obtained.

Contents of ibtree.Tree

 [1,]      100    95.122   89.932    85.21    80.02
 [2,]        0   105.13   100        95.112   89.926
 [3,]        0     0      110.05    105.14   100
 [4,]        0     0        0       115.07   110.06
 [5,]        0     0        0         0      119.91


Contents of ibtree.prob

 [1,]      0.56274   0.58666   0.54526   0.58865
 [2,]      0         0.58921   0.56254   0.58582
 [3,]      0         0         0.57753   0.58956
 [4,]      0         0         0         0.59625


Contents of ibtree.lb

 [1,]      1         0.43399   0.17804   0.080359   0.032809
 [2,]      0         0.55854   0.48043   0.30495    0.17231
 [3,]      0         0         0.32664   0.40521    0.34238
 [4,]      0         0         0         0.18723    0.31214
 [5,]      0         0         0         0          0.1108

The quantlet IBTlocsigma needs the following parameters to compute the implied local volatilities in each node of the tree: $\tt {ptree}$ - the stock prices of the nodes generated by IBTdk or IBTbc, $\tt {prob}$ - the transition probability tree, $\tt {m}$ - the highest desired level, $\tt {deltat}$ - the annualized length of one time step. The output is a 3 column matrix, which consists of: i) the stock price at some nodes of the implied binomial tree, ii) time to expiration, and iii) the estimated implied local volatility at these nodes.

The quantlet IBTvolaplot plots the implied volatility in the implied binomial tree as a function of strike and time to expiration. The following input parameters are required: $\tt {loc}$ - implied local volatilities computed through IBTlocsigma , $\tt {step}$ - the bandwidth of the time interval, $\tt {startpoint}$ and $\tt {endpoint}$ - the lowest and the highest strike dimensions of the volatility surface, $\tt {m}$ - the number of steps to be estimated.

The following example fits an implied five-year tree with 20 levels. The implied local volatility $\sigma_{loc}(S,\tau)$ in the implied tree at different time to expirations and stock price levels is presented in Figure (11.25). The plot confirms the expected result, that the implied local volatility decreases with stock price and increases with time to expiration.

library("finance")
 proc(sigma)=volafunc(K, S, time)
 sigma=0.1+(S-K)/S/10*0.5
 endp
 r=0.03                 ; annualized risk-free interest rate
 S=100                  ; initial underlying asset price
 lev=20                 ; number of time steps
 expiration=5           ; annualized time to expiration
 ibtree=IBTdk(S,r,lev,expiration,"volafunc")
 ptree=ibtree.Tree      ; implied tree of stock prices
 prob=ibtree.prob       ; tree of transition probabilities
 deltat=expiration/lev  ; bandwidth of one time step
 m=20                   ; highest level
 loc=IBTlocsigma(ptree,prob,m,deltat)

 startpoint=50          ; lowest strike bound
 endpoint=150           ; highest strike bound
 n=10                   ; number of estimated steps
 step=0.5               ; bandwidth of one time step
 IBTvolaplot(loc,step,startpoint,endpoint,n)

XLGfindex17.xpl

$\parbox{9cm}{\vspace{-2cm}\caption{\small Implied binomial local volatility \ surface using Derman and Kani IBT.}}$

The Barle and Cakici (1998) method can be used in exactly the same way as the Derman and Kani (1994) method. The following output shows the one year stock price tree, the transition probability tree and the tree of Arrow-Debreu prices, when as in the above example, the quantlet IBTdk is replaced by IBTbc and all other parameters remain the same. The local volatility generated by Barle and Cakici IBT is plotted in Figure (11.26).

Contents of ibtree.Tree

 [1,]      100    96.827   90.526   87.603   82.002
 [2,]        0   104.84   101.51    97.731   93.077
 [3,]        0     0      112.23   107.03   103.05
 [4,]        0     0        0      117.02   112.93
 [5,]        0     0        0        0      123.85


Contents of ibtree.prob

 [1,]      0.49006   0.63991   0.35597   0.56528
 [2,]      0         0.38389   0.48864   0.54064
 [3,]      0         0         0.60523   0.48462
 [4,]      0         0         0         0.45512


Contents of ibtree.lb

 [1,]      1         0.50613   0.18089   0.11563    0.049891
 [2,]      0         0.4864    0.61889   0.37802    0.23722
 [3,]      0         0         0.18533   0.37277    0.39353
 [4,]      0         0         0         0.11133    0.23951
 [5,]      0         0         0         0          0.050289

$\parbox{9cm}{\vspace{-2cm}\caption{\small Implied binomial local volatility surface using Barle and Cakici IBT.}}$

11.5.2.2 Derman and Kani Algorithm

Within an implied binomial tree framework, stock prices, transition probabilities, and Arrow Debreu prices at each node are calculated iteratively level by level. The following describes the construction of implied binomial trees using the Derman and Kani (1994) approach.

Assuming that $n$ levels of the tree have already been constructed, the following explains the construction of the next level, $(n+1)$, of the implied binomial tree, which is illustrated in Figure 11.27. The node $i$, for $i=1...n$, at level $n$ of the implied tree is denoted with $(n,i)$. As in the case of the regular binomial tree, the asset price $S_{n,i}$ in node $(n,i)$ at time $t_n$, can either branch upwards to the node $(i+1)$ with the stock price $S_{n+1,i+1}$, or downwards to the node i with the stock price $S_{n+1,i}$ moving from level $n$ to level $n+1$ of the tree.

The Arrow-Debreu price at node $(n,i)$, denoted as $\lambda_{n,i}$ (Figure  11.27), is the price of an option that pays one unit payoff in one and only one state $i$ at level $n$, otherwise it pays zero. The Arrow-Debreu price is computed by forward induction, as the sum over all paths, from the root of the tree to node $(n,i)$, of the product of transition probabilities at each node, in each path, leading to node $(n,i)$, discounted with the risk-free interest rate.

$\parbox{8cm}{\caption{\small Constructing level $(n+1)$\ of the implied binomial tree.}}$

The next step involves:

1.

choosing the positions of the new $n+1$ nodes at time $t_{n+1}$,

2.

choosing the n "up" probabilities: $p_{n,n}$, $p_{n,n-1}$,.., $p_{n,i}$,.., $p_{n,1}$, between times $t_n$ and $t_{n+1}$.

These choices provide $2n+1$ degrees of freedom. To fulfill the risk-neutrality condition, the expected value of the underlying price $E[S_{n,i}]$ for the next period must equal its forward price:

$$E[S_{n,i}]=p_{n,i}S_{n+1,i+1}+(1-p_{n,i})S_{n+1,i}=F_{i}=exp\{(r-\delta)\Delta t\}S_{n,i},$$ (11.69)

where $F_{i}=exp\{(r-\delta)\Delta tS_{n,i}$ is the forward price corresponding to $S_{n,i}$, $r$ is the continuous interest rate, $\delta$ is the dividend yield and $\Delta t$ is the time step from $t_n$ to $t_{n+1}$. There are $n$ of these forwards equations, one for each $i$. This uses $n$ degrees of freedom.

The tree is also constructed to insure that $n$ independent European vanilla options - $C(K,t_{n+1})$ for call and $P(K,t_{n+1})$ for put - with strike $K=S_{n,i}$ and expiring at time $t_{n+1}$ are priced correctly, i.e. the theoretical values of these options should match their market prices (Derman and Kani; 1994), which uses an additional $n$ degrees of freedom. The theoretical binomial value of any option with strike $K$ and expiration at $t_{n+1}$, is the sum over all nodes $i$ at the $(n+1)$th level, of the transition probabilities of reaching each node $(n+1,i)$ multiplied by the payoff there and discounted with the risk-free interest rate:

$$C(K,t_{n+1})=e^{-r\Delta t}\sum^{n+1}_i\left\{\lambda_{n,i}p_{n,i}+\lambda_{n,i+1}\left(1-p_{n,i+1}\right)\right\}max\left(S_{n+1,i+1}-K,0\right)$$ (11.70)

$$P(K,t_{n+1})=e^{-r\Delta t}\sum^{n+1}_i\left\{\lambda_{n,i}p_{n,i}+\lambda_{n,i+1}\left(1-p_{n,i+1}\right)\right\}max\left(K-S_{n+1,i+1},0\right)$$ (11.71)

All $\lambda_{n,1}$ are known, because early tree nodes and their transition probabilities have already been implied out at level $n$. The market price of each option, $C(K,t_{n+1})$ or $P(K,t_{n+1})$, is obtained by interpolation based on a CRR binomial tree with constant volatility. This constant volatility, is the implied Black-Scholes volatility from known market option prices.

This construction leads to $2n$ equations: $n$ for the expected value of the underlying as in (11.69) and $n$ for the option prices as in (11.70) and (11.71). There are $2n+1$ unknowns: (n+1) stock prices in nodes at level (n+1) of the tree and n transition probabilities. Hence, there is only one degree of freedom left, which is used to ensure that the center node in level $n$ equals the current underlying price. Solving the equations, the tree is advanced only by one time step. The ITB is constructed by repeating this procedure for each time step. Then all stock prices, transition probabilities and Arrow-Debreu prices at any node in the tree will be known.

The implied local volatility $\sigma_{loc}(S_{n,i},m\Delta t)$ that describes the structure of the second moment of the underlying process at any level $m$ of the tree can then be calculated as a discrete approximation of the following conditional variance

$$\sigma_{loc}(S,m\Delta t)=Var\left(logS_{t+\tau}\vert S_t=S\right),$$

at $S=S_{n,i}$ and $\tau=m\Delta t$. The formulas for the discrete estimation of this implied volatility, together with a detailed explanation is given in Härdle and Zheng (2001).

One problem with this approach, is that negative probabilities sometimes arise. When a particular probability turns out to be negative, it is necessary to introduce a rule to override the option price responsible for this negative probability. Another shortcoming is that calculating interpolated option prices by the CRR is computationally intensive.

Barle and Cakici (1998) proposed an improvement on the Derman and Kani (1994) algorithm. The major modification is that for the choice of the central node, their algorithm takes the risk-free interest rate into account. A detailed explanation of the Barle and Cakici (1998) algorithm can be found in Härdle and Zheng (2001).

11.5.3 Implied Trinomial Trees

Implied tree models account for the volatility smile and attempt to price options consistent with the market price. They can be constructed in various ways. Implied binomial trees as discussed in subsection (11.5.2) have just enough parameters, node prices and transition probabilities to fit the smile. In contrast, a trinomial tree has by construction more parameters, since within one single node the stock price can move to one of three possible future values, each with its own respective probability (Figure 11.28). For example at node $i$, at time $t_n$, there are five unknown parameters: two transition probabilities $p_{n,i}$, $q_{n,i}$ and three new node prices $S_i$, $S_{i+1}$, and $S_{i+2}$.

In a risk-neutral trinomial tree, there are two constrains concerning the expected value and the variability of the stock price for these five unknown parameters (Derman, Kani and Chriss; 1996). Consequently, there are three degrees of freedom, which can be used to freely specify three of the parameters, $S_i$, $S_{i+1}$, and $S_{i+2}$, required to fix the tree. No unique trinomial tree, but many equivalent trinomial trees exist, which as $\Delta t$ goes to zero represent the same continuous theory.

The three degrees of freedom can be used to conveniently specify the state space - the underlying price in every node - and allow the transition probabilities to vary as smoothly as possible across the tree. In other words, there is total freedom over the choice of the state space of an implied trinomial tree. This flexibility is a major advantage of using trinomial trees.

$\parbox{8cm}{\caption{\small A single s... ...al tree at $t_0$. \ The sum of the three transition probabilities equals one.}}$

A standard trinomial tree represents a constant volatility world and is constructed out of a regular mesh (Figure 11.29). An implied trinomial tree has an irregular mesh, confirming the variation of local volatility with level and time across the tree (Figure 11.30).

$\parbox{6.2cm}{ \ \includegraphics[widt... ...picwidth]{TT.ps} \ \caption{\small Standard trinomial tree.}\cite{de:ka:ch:96}}$ $\parbox{6.1cm}{ \ \includegraphics[widt... ...fpicwidth]{ITT.ps} \caption{\small Implied trinomial tree.}\cite{de:ka:ch:96}}$

An implied trinomial tree is usually constructed by two steps (Derman, Kani and Chriss; 1996). In the first step, the initial state space is selected. When implied volatility varies slowly with strike and expiration, a constant volatility trinomial tree can be used. This can be done by combining the two steps of the CRR binomial tree into a single step of a trinomial tree as illustrated in Figure (11.31). Other methods used to build a constant volatility trinomial tree are presented in Derman, Kani and Chriss (1996). If volatility varies significantly with strike and expiration, a trinomial space with proper skew and term structure must be chosen.

$\parbox{10cm}{\caption{\small Combining two steps of a CCR binomial tree.}\cite{de:ka:ch:96}}$

By knowing the location of every node, the market forwards and option prices are used in the second step to fix transition probabilities. This is done iteratively to ensure that all European vanilla options will have theoretical values that match their market prices.

Constructing the tree may result in transition probabilities being negative or greater than one, which is inconsistent with rational option prices and allows arbitrage. In this case, a rule must be defined for overwriting the option price which produces incorrect probabilities.

Komorád (2002) explains in detail how to use XploRe for constructing implied trinomial trees. Since this is included in Tutorials-Finance in XploRe , these quantlets are introduced briefly.

ITT is used to compute the state space of an implied tree, the probability matrices, the Arrow-Debreu prices and the local volatility matrix. It uses the quantlet ITTcrr to compute the option prices. ITTcrr builds up a constant volatility trinomial tree by combining two steps of a CRR binomial tree.

The simplest way to display results is to apply the quantlet plotITT . Once the ITT is constructed, plotITT offers the possibility to plot the state space of the ITT, the tree of transition probabilities, the tree of local volatilities, the tree of Arrow Debreu prices and the state price density.

More advanced features allow the user to integrate the plot of any trinomial tree with other graphical objects, into one graph. grITTstsp returns the state space of an implied trinomial tree with transition probabilities as a graphical object (Komorád; 2002), whereas grITTspd generates a state price density of an implied trinomial tree (see Komorád (2002) for a detailed explanation and examples).