We also want to perform statistical inference based on the smoothers.
As for parametric regression, we want to construct confidence bands
and prediction intervals based on the smooth curve. Given a new car
that weighs ![]() pounds, what is its fuel economy? Tests of
hypotheses can also be posed: for example, is the curvature observed
in Fig. 5.2 significant, or would a linear regression be
adequate? Given different classifications of car (compact, sporty,
minivan etc.) is there differences among the categories that cannot
be explained by weight alone?
pounds, what is its fuel economy? Tests of
hypotheses can also be posed: for example, is the curvature observed
in Fig. 5.2 significant, or would a linear regression be
adequate? Given different classifications of car (compact, sporty,
minivan etc.) is there differences among the categories that cannot
be explained by weight alone?
All smoothing methods have one or more smoothing parameters:
parameters that control the `amount' of smoothing being performed.
For example, the bandwidth ![]() in the kernel and local regression
estimates. Typically, bandwidth selection methods are based on an
estimate of some goodness-of-fit criterion. Bandwidth selection is
a special case of model selection, discussed more deeply in
Chap. III.1.
in the kernel and local regression
estimates. Typically, bandwidth selection methods are based on an
estimate of some goodness-of-fit criterion. Bandwidth selection is
a special case of model selection, discussed more deeply in
Chap. III.1.
How should smoothing parameters be used? At one extreme, there is full automation: optimization of the goodness-of-fit criterion produces a single `best' bandwidth. At the other extreme is purely exploratory and graphical methods, using goodness-of-fit as a guide to help choose the best method.
Automation has the advantage that it requires much less work; a computer can be programmed to perform the optimization. But the price is a lack of reliability: fits with very different bandwidths can produce similar values of the goodness-of-fit criterion. The result is either high variability (producing fits that look undersmoothed) or high bias (producing fits that miss obvious features in the data).
Cross validation (CV) focuses on the prediction problem:
if the fitted regression curve is used to predict new observations,
how good will the prediction be? If a new observation is made at
![]() , and the response
, and the response ![]() is predicted by
is predicted by
![]() , what is the prediction error? One measure is
, what is the prediction error? One measure is
The method of CV can be used to estimate this quantity. In turn, each
observation ![]() is omitted from the dataset, and is
`predicted' by smoothing the remaining
is omitted from the dataset, and is
`predicted' by smoothing the remaining ![]() observations. This leads
to the CV score
observations. This leads
to the CV score
Formally computing each of the leave-one-out regression estimates
![]() would be highly computational, and so at
a first glance computation of the CV score (5.17) looks
prohibitively expensive. But there is a remarkable simplification,
valid for nearly all common linear smoothers (and all those discussed
in Sect. 5.2):
would be highly computational, and so at
a first glance computation of the CV score (5.17) looks
prohibitively expensive. But there is a remarkable simplification,
valid for nearly all common linear smoothers (and all those discussed
in Sect. 5.2):
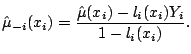 |
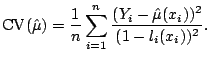 |
Generalized cross validation
(GCV) replaces each of the influence values ![]() by the average,
by the average,
![]() . This leads to
. This leads to
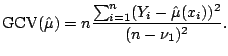 |
![\includegraphics[width=8cm]{text/3-5/lrfig3.eps}](img4163.gif)
|
Figure 5.4 shows the GCV scores for the fuel economy
dataset, and using kernel and local linear smoothers with a range of
bandwidths. Note the construction of the plot: the fitted degrees of
freedom ![]() are used as the
are used as the ![]() axis. This allows us to
meaningfully superimpose and compare the GCV curves arising from
different smoothing methods. From right to left, the points marked
`0' represent a kernel smoother with
axis. This allows us to
meaningfully superimpose and compare the GCV curves arising from
different smoothing methods. From right to left, the points marked
`0' represent a kernel smoother with
![]() and
and
![]() , and points marked `
, and points marked `![]() ' represent a local linear smoother with
' represent a local linear smoother with
![]() and
and ![]() .
.
The interpretation of Fig. 5.4 is that for any fixed degrees
of freedom, the local linear fit outperforms the kernel fit. The best
fits obtained are the local linear, with ![]() to 3.5 degrees of
freedom, or
to 3.5 degrees of
freedom, or ![]() between
between ![]() and
and ![]() .
.
A risk function measures the distance between the true regression function and the estimate; for example,
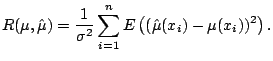 |
(5.18) |
Instead, the risk must be estimated. An unbiased estimate is
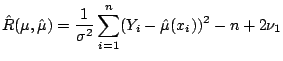 |
The unbiased risk estimate can be used similarly to GDV. One computes
![]() for a range of different fits
for a range of different fits ![]() ,
and plots the resulting risk estimates versus the degrees of
freedom. Fits producing a small risk estimate are considered best.
,
and plots the resulting risk estimates versus the degrees of
freedom. Fits producing a small risk estimate are considered best.
An entirely different class of bandwidth selection methods, often termed plug-in methods, attempt to directly estimate a risk measure by estimating the bias and variance. The method has been developed mostly in the context of kernel density estimation, but adaptations to kernel regression and local polynomial regression can be found in [7] and [24].
Again focusing on the squared-error risk, we have the bias-variance decomposition
There are many variants of the plug-in idea in the statistics literature. Most simplify the risk function using asymptotic approximations such as (5.13) and (5.15) for the bias and variance; making these substitutions in (5.19) gives
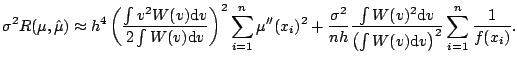 |
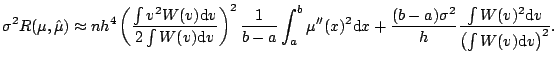 |
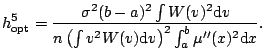 |
Evaluation of
![]() requires substitution of estimates for
requires substitution of estimates for
![]() and of
and of ![]() . The
estimate (5.16) can be used to estimate
. The
estimate (5.16) can be used to estimate ![]() , but
estimating
, but
estimating
![]() is more problematic. One
technique is to estimate the second derivative using a `pilot'
estimate
of the smooth, and then use the estimate
is more problematic. One
technique is to estimate the second derivative using a `pilot'
estimate
of the smooth, and then use the estimate
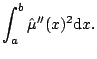 |
But the use of a pilot estimate to estimate the second derivative is
problematic. The pilot estimate itself has a bandwidth that has to be
selected, and the estimated optimal bandwidth
![]() is
highly sensitive to the choice of pilot bandwidth. Roughly, if the
pilot estimate smooths out important features of
is
highly sensitive to the choice of pilot bandwidth. Roughly, if the
pilot estimate smooths out important features of ![]() , so will the
estimate
, so will the
estimate ![]() with bandwidth
with bandwidth
![]() . More discussion
of this point may be found in [20].
. More discussion
of this point may be found in [20].
Inferential procedures for smoothers include the construction of confidence bands for the true mean function, and procedures to test the adequacy of simpler models. In this section, some of the main ideas are briefly introduced; more extensive discussion can be found in the books [3], [11], [12] and [21].
If the errors
![]() are normally distributed, then confidence
intervals for the true mean can be constructed as
are normally distributed, then confidence
intervals for the true mean can be constructed as
Consider the problem of testing for the adequacy of a linear model.
For example, in the fuel economy dataset of Figs. 5.1
and 5.2, one may be interested in knowing whether a linear
regression,
![]() is adequate, or alternatively whether the
departure from linearity indicated by the smooth is significant. This
hypothesis testing problem can be stated as
is adequate, or alternatively whether the
departure from linearity indicated by the smooth is significant. This
hypothesis testing problem can be stated as
In analogy with the theory of linear models, an ![]() ratio can be formed
by fitting both the null and alternative models, and considering the
difference between the fits. Under the null model, parametric least
squares is used; the corresponding fitted values are
ratio can be formed
by fitting both the null and alternative models, and considering the
difference between the fits. Under the null model, parametric least
squares is used; the corresponding fitted values are
![]() where
where
![]() is the hat matrix for the least squares fit. Under
the alternative model, the fitted values are
is the hat matrix for the least squares fit. Under
the alternative model, the fitted values are
![]() , where
, where
![]() is the hat matrix for a local linear regression. An
is the hat matrix for a local linear regression. An
![]() ratio can then be formed as
ratio can then be formed as
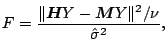 |
What is the distribution of ![]() when
when ![]() is true? Since
is true? Since
![]() is not a perpendicular projection operator, the numerator does not
have a
is not a perpendicular projection operator, the numerator does not
have a ![]() distribution, and
distribution, and ![]() does not have an exact
does not have an exact
![]() distribution. None-the-less, we can use an approximating
distribution. None-the-less, we can use an approximating
![]() distribution. Based on a one-moment approximation, the degrees of
freedom are
distribution. Based on a one-moment approximation, the degrees of
freedom are ![]() and
and
![]() .
.
Better approximations are obtained using the two-moment Satterwaite
approximation,
as described in [5]. This method matches both the mean and
variance of chi-square approximations to the numerator and
denominator. Letting
![]() , the numerator degrees
of freedom for the
, the numerator degrees
of freedom for the ![]() distribution are given by
distribution are given by
![]() . A similar adjustment is made to the denominator
degrees of freedom. Simulations reported in [5] suggest
the two-moment approximation is adequate for setting critical values.
. A similar adjustment is made to the denominator
degrees of freedom. Simulations reported in [5] suggest
the two-moment approximation is adequate for setting critical values.
For the fuel economy dataset, we obtain ![]() ,
,
![]() and
and
![]() . Using the
one-moment approximation, the
. Using the
one-moment approximation, the ![]() -value is
-value is ![]() . The
two-moment approximation gives a
. The
two-moment approximation gives a ![]() -value of
-value of ![]() . Both
methods indicate that the nonlinearity is significant, although there
is some discrepancy between the
. Both
methods indicate that the nonlinearity is significant, although there
is some discrepancy between the ![]() -values.
-values.
The ![]() -tests in the previous section are approximate, even when the
errors
-tests in the previous section are approximate, even when the
errors
![]() are normally distributed. Additionally, the
degrees-of-freedom computations (particularly for the two-moment
approximation) require
are normally distributed. Additionally, the
degrees-of-freedom computations (particularly for the two-moment
approximation) require ![]() computations, which is prohibitively
expensive for
computations, which is prohibitively
expensive for ![]() more than a few hundred.
more than a few hundred.
An alternative to the ![]() approximations is to simulate the null
distribution of the
approximations is to simulate the null
distribution of the ![]() ratio. A bootstrap method
(Chap. III.2) performs the
simulations using the empirical residuals to approximate the true
error distribution:
ratio. A bootstrap method
(Chap. III.2) performs the
simulations using the empirical residuals to approximate the true
error distribution:
This procedure is repeated a large number of times (say ![]() ) and
tabulation of the resulting
) and
tabulation of the resulting ![]() values provides an estimate of
the true distribution of the
values provides an estimate of
the true distribution of the ![]() ratio.
ratio.
Remark. Since the degrees of freedom do not change with the
replication, there is no need to actually compute the normalizing
constant. Instead, one can simply work with the modified ![]() ratio,
ratio,
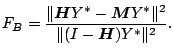 |
![\includegraphics[width=7.7cm]{text/3-5/lrfigb.eps}](img4212.gif)
|
Figure 5.5 compares the bootstrap distribution of the ![]() ratio and the 1 and 2 moment
ratio and the 1 and 2 moment ![]() approximations for the fuel economy
dataset. The bootstrap method uses
approximations for the fuel economy
dataset. The bootstrap method uses ![]() bootstrap
replications, and the density is estimated using the Local Likelihood
method (Sect. 5.5.2 below). Except at the left end-point,
there is generally good agreement between the bootstrap density and
the two-moment density. The upper
bootstrap
replications, and the density is estimated using the Local Likelihood
method (Sect. 5.5.2 below). Except at the left end-point,
there is generally good agreement between the bootstrap density and
the two-moment density. The upper ![]() quantiles are 3.21
based on the two-moment approximation, and 3.30 based on the
bootstrap sample. The one-moment approximation has a critical value of
3.90. Based on the observed
quantiles are 3.21
based on the two-moment approximation, and 3.30 based on the
bootstrap sample. The one-moment approximation has a critical value of
3.90. Based on the observed ![]() , the bootstrap
, the bootstrap
![]() -value is 0.0023, again in close agreement with the
two-moment method.
-value is 0.0023, again in close agreement with the
two-moment method.