This powerful algorithm provides a general approach for producing
a correlated sequence of draws from the target density that may be
difficult to sample by a classical independence method. The goal is to
simulate the ![]() -dimensional distribution
-dimensional distribution
![]() ,
,
![]() that has density
that has density
![]() with respect to some dominating measure. To
define the algorithm, let
with respect to some dominating measure. To
define the algorithm, let
![]() denote a source density for a candidate draw
denote a source density for a candidate draw
![]() given the current value
given the current value ![]() in the sampled sequence. The density
in the sampled sequence. The density
![]() is referred to as the
proposal or candidate generating density. Then, the M-H algorithm is
defined by two steps: a first step in which a proposal value is drawn
from the
candidate generating density and a second step in which the proposal
value is accepted as the next iterate in the Markov chain according to
the probability
is referred to as the
proposal or candidate generating density. Then, the M-H algorithm is
defined by two steps: a first step in which a proposal value is drawn
from the
candidate generating density and a second step in which the proposal
value is accepted as the next iterate in the Markov chain according to
the probability
![]() , where
, where
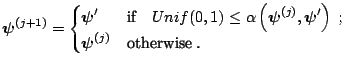 |
Typically, a certain number of values (say ![]() ) at the start of
this sequence are discarded after which the chain is assumed to have
converged to it invariant distribution and the subsequent draws are
taken as approximate variates from
) at the start of
this sequence are discarded after which the chain is assumed to have
converged to it invariant distribution and the subsequent draws are
taken as approximate variates from ![]() . Because theoretical
calculation of the
burn-in is not easy it is important that the proposal density is
chosen to ensure that the chain makes large moves through the support
of the invariant distribution without staying at one place for many
iterations. Generally, the empirical behavior of the M-H output is
monitored by the autocorrelation time of each component of
. Because theoretical
calculation of the
burn-in is not easy it is important that the proposal density is
chosen to ensure that the chain makes large moves through the support
of the invariant distribution without staying at one place for many
iterations. Generally, the empirical behavior of the M-H output is
monitored by the autocorrelation time of each component of
![]() and by the
acceptance rate, which is the proportion of times a move is made as
the sampling proceeds.
and by the
acceptance rate, which is the proportion of times a move is made as
the sampling proceeds.
One should observe that the target density appears as a ratio in the
probability
![]() and
therefore the algorithm can be implemented without knowledge of the
normalizing constant of
and
therefore the algorithm can be implemented without knowledge of the
normalizing constant of
![]() . Furthermore, if the
candidate-generating density is symmetric, i.e.
. Furthermore, if the
candidate-generating density is symmetric, i.e.
![]() , the acceptance probability
only contains the ratio
, the acceptance probability
only contains the ratio
![]() ; hence, if
; hence, if
![]() , the chain moves to
, the chain moves to
![]() ,
otherwise it moves with probability given by
,
otherwise it moves with probability given by
![]() . The latter is the
algorithm originally proposed by [39]. This version of the
algorithm is illustrated in
Fig. 3.1.
. The latter is the
algorithm originally proposed by [39]. This version of the
algorithm is illustrated in
Fig. 3.1.
![\includegraphics[width=9cm]{text/2-3/fig2.eps}](img1160.gif)
|
Different proposal densities give rise to specific versions of the
M-H algorithm, each with the correct invariant distribution ![]() . One family of candidate-generating densities is given by
. One family of candidate-generating densities is given by
![]() . The candidate
. The candidate
![]() is thus drawn
according to the process
is thus drawn
according to the process
![]() , where
, where
![]() follows the distribution
follows the distribution ![]() . Since the candidate is equal to the
current value plus noise, this case is called
a random walk M-H chain. Possible choices for
. Since the candidate is equal to the
current value plus noise, this case is called
a random walk M-H chain. Possible choices for ![]() include the
multivariate normal density and the multivariate-
include the
multivariate normal density and the multivariate-![]() . The random walk
M-H chain is perhaps the simplest version of the M-H algorithm (and
was the one used by [39]) and popular in applications. One
has to be careful, however, in setting the variance of
. The random walk
M-H chain is perhaps the simplest version of the M-H algorithm (and
was the one used by [39]) and popular in applications. One
has to be careful, however, in setting the variance of
![]() ;
if it is too large it is possible that the chain may remain stuck at
a particular value for many iterations while if it is too small the
chain will tend to make small moves and move inefficiently through the
support of the target distribution. In both cases the generated draws
that will be highly serially correlated. Note that when
;
if it is too large it is possible that the chain may remain stuck at
a particular value for many iterations while if it is too small the
chain will tend to make small moves and move inefficiently through the
support of the target distribution. In both cases the generated draws
that will be highly serially correlated. Note that when ![]() is
symmetric,
is
symmetric,
![]() and the probability of move
only contains the ratio
and the probability of move
only contains the ratio
![]() . As mentioned earlier, the same reduction occurs if
. As mentioned earlier, the same reduction occurs if
![]() .
.
[32] considers a second family of candidate-generating
densities that are given by the form
![]() . [59]
refers to this as an
independence M-H chain because, in contrast to the random walk chain,
the candidates are drawn independently of the current
location
. [59]
refers to this as an
independence M-H chain because, in contrast to the random walk chain,
the candidates are drawn independently of the current
location
![]() . In this case, the probability of move
becomes
. In this case, the probability of move
becomes
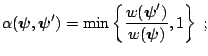 |
Chib and Greenberg (1994, 1995)
discuss a way of formulating proposal densities in the context of time
series autoregressive-moving average models that has a bearing on the
choice of proposal density for the independence M-H chain. They
suggest matching the proposal density to the target at the mode by
a multivariate normal or multivariate-![]() distribution with location
given by the mode of the target and the dispersion given by inverse of
the Hessian evaluated at the mode. Specifically, the parameters of the
proposal density are taken to be
distribution with location
given by the mode of the target and the dispersion given by inverse of
the Hessian evaluated at the mode. Specifically, the parameters of the
proposal density are taken to be
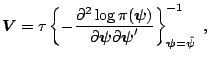 |
(3.11) |
Another way to generate proposal values is through a Markov chain
version of the accept-reject method. In this version, due to
[59], and considered in detail by [14], a pseudo
accept-reject step is used to generate candidates for an M-H
algorithm. Suppose ![]() is a known constant and
is a known constant and
![]() a source density. Let
a source density. Let
![]() denote the set of value for which
denote the set of value for which
![]() dominates the target density and assume that this
set has high probability under
dominates the target density and assume that this
set has high probability under
![]() . Given
. Given
![]() , the next value
, the next value
![]() is obtained as follows: First, a candidate
value
is obtained as follows: First, a candidate
value
![]() is obtained, independent of the current
value
is obtained, independent of the current
value
![]() , by applying the accept-reject algorithm with
, by applying the accept-reject algorithm with
![]() as the ''pseudo dominating'' density. The candidates
as the ''pseudo dominating'' density. The candidates
![]() that are
produced under this scheme have density
that are
produced under this scheme have density
![]() . If we let
. If we let
![]() then it can be shown
that the M-H probability of move is given by
then it can be shown
that the M-H probability of move is given by
In the M-H algorithm the transition kernel of the chain is given by
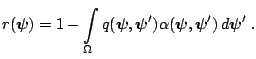 |
[14] provide a way to derive and interpret the probability
of move
![]() . Consider the
proposal density
. Consider the
proposal density
![]() . This
proposal density
. This
proposal density ![]() is not likely to be reversible for
is not likely to be reversible for ![]() (if it
were then we would be done and M-H sampling would not be
necessary). Without loss of generality, suppose that
(if it
were then we would be done and M-H sampling would not be
necessary). Without loss of generality, suppose that
![]() implying that the rate of transitions from
implying that the rate of transitions from
![]() to
to
![]() exceed those in the reverse direction. To
reduce the transitions from
exceed those in the reverse direction. To
reduce the transitions from
![]() to
to
![]() one can introduce a function
one can introduce a function
![]() such that
such that
![]() . Solving
for
. Solving
for
![]() yields the
probability of move in the M-H algorithm. This calculation reveals
the important point that the function
yields the
probability of move in the M-H algorithm. This calculation reveals
the important point that the function
![]() is reversible by
construction, i.e., it satisfies the condition
is reversible by
construction, i.e., it satisfies the condition
It is not difficult to provide conditions under which the Markov chain
generated by the M-H algorithm satisfies the conditions of
Propositions 1-2. The conditions of Proposition 1 are satisfied by
the M-H chain if
![]() is
positive for
is
positive for
![]() and continuous
and the set
and continuous
and the set
![]() is connected. In addition, the conditions
of Proposition 2 are satisfied if
is connected. In addition, the conditions
of Proposition 2 are satisfied if ![]() is not reversible (which is the
usual situation) which leads to a chain that is aperiodic. Conditions
for ergodicity, required for use of the central limit theorem, are
satisfied if in addition
is not reversible (which is the
usual situation) which leads to a chain that is aperiodic. Conditions
for ergodicity, required for use of the central limit theorem, are
satisfied if in addition ![]() is bounded. Other similar conditions
are provided by [50].
is bounded. Other similar conditions
are provided by [50].
To illustrate the M-H algorithm, consider the
binary response data in Table 3.1, taken from Fahrmeir and Tutz
(1997),
on the occurrence or non-occurrence of infection following birth by
caesarean section. The response variable ![]() is one if the caesarean
birth resulted in an infection, and zero if not. There are three
covariates:
is one if the caesarean
birth resulted in an infection, and zero if not. There are three
covariates: ![]() , an indicator of whether the caesarean was
non-planned;
, an indicator of whether the caesarean was
non-planned; ![]() , an indicator of whether risk factors were
present at the time of birth and
, an indicator of whether risk factors were
present at the time of birth and ![]() , an indicator of whether
antibiotics were given as a prophylaxis. The data in the table
contains information from
, an indicator of whether
antibiotics were given as a prophylaxis. The data in the table
contains information from ![]() births. Under the column of the
response, an entry such as
births. Under the column of the
response, an entry such as ![]() means that there were
means that there were ![]() deliveries with covariates
deliveries with covariates ![]() of whom
of whom ![]() developed an
infection and
developed an
infection and ![]() did not.
did not.
Suppose that the probability of infection for the ![]() th birth
th birth
![]() is
is
| (3.16) | |
| (3.17) |
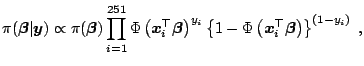 |
To define the proposal density, let
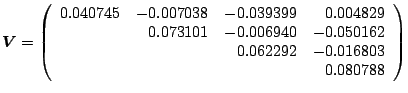 |
| (3.18) |
| Prior | Posterior | |||||
| Mean | Std dev | Mean | Std dev | Lower | Upper | |
|
|
|
|
||||
|
|
|
|
||||
As expected, both the first and second covariates increase the probability of infection while the third covariate (the antibiotics prophylaxis) reduces the probability of infection.
To get an idea of the form of the posterior density we plot in Fig. 3.1 the four marginal posterior densities. The density plots are obtained by smoothing the histogram of the simulated values with a Gaussian kernel. In the same plot we also report the autocorrelation functions (correlation against lag) for each of the sampled parameter values. The autocorrelation plots provide information of the extent of serial dependence in the sampled values. Here we see that the serial correlations start out high but decline to almost zero by lag twenty.
![\includegraphics[width=9cm]{text/2-3/fig1press.eps}](img1253.gif)
|
| Prior | Posterior | |||||
| Mean | Std dev | Mean | Std dev | Lower | Upper | |
|
|
|
|
||||
|
|
|
|
||||
To see the difference in results, the M-H algorithm is next
implemented with a tailored proposal density. In this scheme one
utilizes both
![]() and
and
![]() that were
defined above. We let the proposal density be
that were
defined above. We let the proposal density be
![]() ,
a multivariate-
,
a multivariate-![]() density with fifteen degrees of freedom. This
proposal density is similar to the random-walk proposal except that
the distribution is centered at the fixed point
density with fifteen degrees of freedom. This
proposal density is similar to the random-walk proposal except that
the distribution is centered at the fixed point
![]() . The prior-posterior summary based on
. The prior-posterior summary based on ![]() draws of the M-H algorithm with this proposal density is given in
Table 3.3. We see that the marginal posterior moments are
similar to those in Table 3.1. The marginal posterior
densities are reported in the top panel of
Fig. 3.2. These are virtually identical to those
computed using the random-walk M-H algorithm. The most notable
difference is in the serial correlation plots which decline much more
quickly to zero indicating that the algorithm is mixing well. The same
information is revealed by the inefficiency factors which are much
closer to one than those from the previous algorithm.
draws of the M-H algorithm with this proposal density is given in
Table 3.3. We see that the marginal posterior moments are
similar to those in Table 3.1. The marginal posterior
densities are reported in the top panel of
Fig. 3.2. These are virtually identical to those
computed using the random-walk M-H algorithm. The most notable
difference is in the serial correlation plots which decline much more
quickly to zero indicating that the algorithm is mixing well. The same
information is revealed by the inefficiency factors which are much
closer to one than those from the previous algorithm.
The message from this analysis is that the two proposal densities produce similar results, with the differences appearing only in the autocorrelation plots (and inefficiency factors) of the sampled draws.
![\includegraphics[width=9cm]{text/2-3/fig2press.eps}](img1270.gif)
|
In applications when the dimension of
![]() is large, it can
be difficult to construct a single block M-H algorithm that converges
rapidly to the target density. In such cases, it is helpful to break
up the variate space into smaller blocks and to then construct
a Markov chain with these smaller blocks. Suppose, for illustration,
that
is large, it can
be difficult to construct a single block M-H algorithm that converges
rapidly to the target density. In such cases, it is helpful to break
up the variate space into smaller blocks and to then construct
a Markov chain with these smaller blocks. Suppose, for illustration,
that
![]() is split into two vector blocks
is split into two vector blocks
![]() . For example, in a regression
model, one block may consist of the regression coefficients and the
other block may consist of the error variance. Next, for each block,
let
. For example, in a regression
model, one block may consist of the regression coefficients and the
other block may consist of the error variance. Next, for each block,
let
With these inputs, one sweep of the multiple-block M-H algorithm is completed by updating each block, say sequentially in fixed order, using a M-H step with the above probabilities of move, given the most current value of the other block.
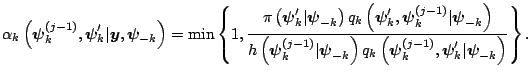 |
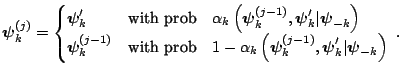 |
The extension of this method to more than two blocks is straightforward.
The transition kernel of the resulting Markov chain is given by the product of transition kernels
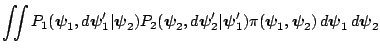 |
||
![$\displaystyle =\int P_{2}(\boldsymbol{\psi}_{2},d\boldsymbol{\psi}_{2}^{\prime}...
...mbol{ \psi}_{1}\right] \pi _{2}(\boldsymbol{\psi}_{2})\,d\boldsymbol{ \psi}_{2}$](img1297.gif) |
||
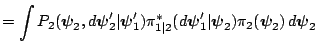 |
||
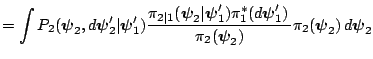 |
||
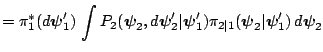 |
||
The implication of this result is that it allows us to take draws in succession from each of the kernels, instead of having to run each to convergence for every value of the conditioning variable.
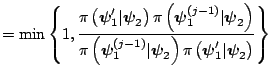 |
||