



Next: 3.5 MCMC Sampling with
Up: 3. Markov Chain Monte
Previous: 3.3 Metropolis-Hastings Algorithm
Subsections
3.4 The Gibbs Sampling Algorithm
The Gibbs sampling algorithm is one of the simplest Markov chain Monte
Carlo algorithms. It was introduced by [26] in the context
of image processing and then discussed in the context of missing data
problems by [58]. The paper by [23] helped to
demonstrate the value of the Gibbs algorithm for a range of problems
in Bayesian analysis.
To define the Gibbs sampling algorithm, let the set of
full conditional distributions be
Now one cycle of the Gibbs sampling algorithm is completed by
simulating
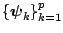 from these distributions,
recursively refreshing the conditioning variables. When
from these distributions,
recursively refreshing the conditioning variables. When 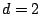 one
obtains the two block Gibbs sampler that appears in
[58]. The Gibbs sampler in which each block is revised in
fixed order is defined as follows.
one
obtains the two block Gibbs sampler that appears in
[58]. The Gibbs sampler in which each block is revised in
fixed order is defined as follows.
Algorithm 3 (Gibbs Sampling)
- Specify an initial value
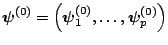 :
:
- Repeat for
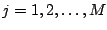 .
.
- Generate
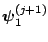 from
from
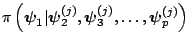
- Generate
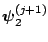 from
from
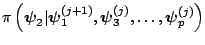

- Generate
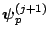 from
from
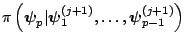 .
.
- Return the values
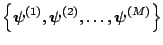 .
.
Figure 3.4:
Gibbs sampling algorithm in two dimensions starting from an initial
point and then completing three iterations
|
|
It follows that the transition density of moving from
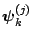 to
to
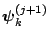 is given by
is given by
since when the 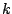 th block is reached, the previous
th block is reached, the previous 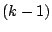 blocks
have been updated. Thus, the transition density of the chain, under
the maintained assumption that
blocks
have been updated. Thus, the transition density of the chain, under
the maintained assumption that 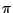 is absolutely continuous, is
given by the product of transition kernels for each block:
is absolutely continuous, is
given by the product of transition kernels for each block:
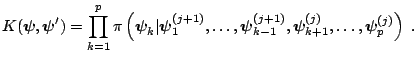 |
(3.23) |
To illustrate the manner in which the blocks are revised, we consider
a two block case, each with a single component, and trace out in
Fig. 3.4 a possible trajectory of the sampling algorithm. The
contours in the plot represent the joint distribution
of
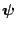 and the labels ''
and the labels ''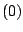 '', ''
'', ''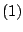 '' etc., denote
the simulated values. Note that one iteration of the algorithm is
completed after both components are revised. Also notice that each
component is revised along the direction of the coordinate axes. This
feature can be a source of problems if the two components are highly
correlated because then the contours get compressed and movements
along the coordinate axes tend to produce small moves. We return to
this issue below.
'' etc., denote
the simulated values. Note that one iteration of the algorithm is
completed after both components are revised. Also notice that each
component is revised along the direction of the coordinate axes. This
feature can be a source of problems if the two components are highly
correlated because then the contours get compressed and movements
along the coordinate axes tend to produce small moves. We return to
this issue below.
The Gibbs transition kernel is invariant by construction. This is
a consequence of the fact that the Gibbs algorithm is a special case
of the multiple-block M-H algorithm which is invariant, as was
established in the last section. Invariance can also be confirmed
directly. Consider for simplicity a two block sampler with transition
kernel density
To check invariance we have to show that
is equal to
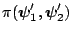 . This holds
because
. This holds
because
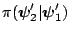 comes out of the integral, and the integral over
comes out of the integral, and the integral over
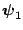 and
and
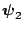 produces
produces
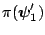 . This
calculation can be extended to any number of blocks. It may be noted
that the Gibbs Markov chain is not reversible. Reversible Gibbs
samplers are discussed by [36].
. This
calculation can be extended to any number of blocks. It may be noted
that the Gibbs Markov chain is not reversible. Reversible Gibbs
samplers are discussed by [36].
Under rather general conditions, the Markov chain generated by the
Gibbs sampling algorithm converges to the target density as the number
of iterations become large. Formally, if we let
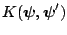 represent the transition density of the Gibbs
algorithm and let
represent the transition density of the Gibbs
algorithm and let
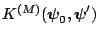 be
the density of the draw
be
the density of the draw
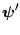 after
after 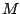 iterations
given the starting value
iterations
given the starting value
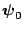 , then
, then
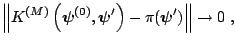 as as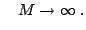 |
(3.24) |
[53] (see also [7]) have shown that the
conditions of Proposition 2 are satisfied under the following
conditions: (1)
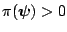 implies there exists an open
neighborhood
implies there exists an open
neighborhood
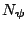 containing
containing
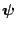 and
and
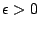 such that, for all
such that, for all
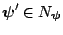 ,
,
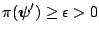 ;
(2)
;
(2)
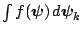 is locally bounded for
all
is locally bounded for
all 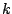 , where
, where
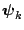 is the
is the 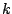 th block of parameters; and
(3) the support of
th block of parameters; and
(3) the support of
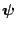 is arc connected.
is arc connected.
These conditions are satisfied in a wide range of problems.
Consider the question of sampling a trivariate normal distribution
truncated to the positive orthant. In particular, suppose that the
target distribution is
where
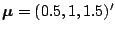 ,
,
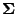 is in equi-correlated form with units on the
diagonal and
is in equi-correlated form with units on the
diagonal and 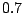 on the off-diagonal,
on the off-diagonal,
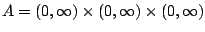 and
and
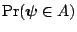 is the
normalizing constant which is difficult to compute. In this case, the
Gibbs sampler is defined with the blocks
is the
normalizing constant which is difficult to compute. In this case, the
Gibbs sampler is defined with the blocks
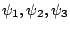 and
the full conditional distributions
and
the full conditional distributions
where each of the these full conditional distributions is univariate
truncated normal restricted to the interval
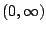 :
:
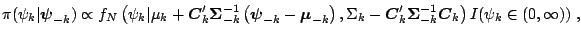 |
(3.25) |
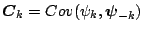 ,
,
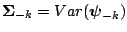 and
and
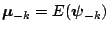 . Figure 3.5 gives the marginal
distribution of each component of
. Figure 3.5 gives the marginal
distribution of each component of 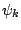 from a Gibbs sampling
run of
from a Gibbs sampling
run of
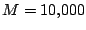 iterations with a burn-in of
iterations with a burn-in of 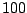 cycles. The
figures includes both the histograms of the sampled values and the
Rao-Blackwellized estimates of the marginal densities (see
Sect. 3.6 below) based on the averaging of (3.25)
over the simulated values of
cycles. The
figures includes both the histograms of the sampled values and the
Rao-Blackwellized estimates of the marginal densities (see
Sect. 3.6 below) based on the averaging of (3.25)
over the simulated values of
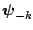 . The agreement
between the two density estimates is close. In the bottom panel of
Fig. 3.5 we plot the autocorrelation function of the sampled
draws. The rapid decline in the autocorrelations for higher lags
indicates that the sampler is mixing well.
. The agreement
between the two density estimates is close. In the bottom panel of
Fig. 3.5 we plot the autocorrelation function of the sampled
draws. The rapid decline in the autocorrelations for higher lags
indicates that the sampler is mixing well.
Figure 3.5:
Marginal distributions of
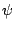 in truncated multivariate normal
example (top panel). Histograms of the sampled values and
Rao-Blackwellized estimates of the densities are shown. Autocorrelation plots
of the Gibbs MCMC chain are in the bottom panel. Graphs are based on
in truncated multivariate normal
example (top panel). Histograms of the sampled values and
Rao-Blackwellized estimates of the densities are shown. Autocorrelation plots
of the Gibbs MCMC chain are in the bottom panel. Graphs are based on
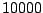 iterations following a burn-in of
iterations following a burn-in of 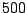 cycles
cycles
|
|




Next: 3.5 MCMC Sampling with
Up: 3. Markov Chain Monte
Previous: 3.3 Metropolis-Hastings Algorithm
![\includegraphics[width=7.3cm]{text/2-3/fig4.eps}](img1321.gif)
![]() to
to
![]() is given by
is given by
![]() and the labels ''
and the labels ''![]() '', ''
'', ''![]() '' etc., denote
the simulated values. Note that one iteration of the algorithm is
completed after both components are revised. Also notice that each
component is revised along the direction of the coordinate axes. This
feature can be a source of problems if the two components are highly
correlated because then the contours get compressed and movements
along the coordinate axes tend to produce small moves. We return to
this issue below.
'' etc., denote
the simulated values. Note that one iteration of the algorithm is
completed after both components are revised. Also notice that each
component is revised along the direction of the coordinate axes. This
feature can be a source of problems if the two components are highly
correlated because then the contours get compressed and movements
along the coordinate axes tend to produce small moves. We return to
this issue below.
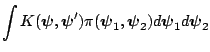
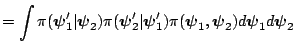
![]() represent the transition density of the Gibbs
algorithm and let
represent the transition density of the Gibbs
algorithm and let
![]() be
the density of the draw
be
the density of the draw
![]() after
after ![]() iterations
given the starting value
iterations
given the starting value
![]() , then
, then
![\includegraphics[width=11cm]{text/2-3/fig5.eps}](img1365.gif)