In designing MCMC simulations, it is sometimes helpful to modify the target distribution by introducing latent variables or auxiliary variables into the sampling. This idea was called data augmentation by [58] in the context of missing data problems. Slice sampling, which we do not discuss in this chapter, is a particular way of introducing auxiliary variables into the sampling, for example see [20].
To fix notations, suppose that
![]() denotes a vector of latent
variables and let the modified target distribution be
denotes a vector of latent
variables and let the modified target distribution be
![]() . If the latent variables are tactically
introduced, the conditional distribution of
. If the latent variables are tactically
introduced, the conditional distribution of
![]() (or sub
components of
(or sub
components of
![]() given
given
![]() may be easy to
derive. Then, a multiple-block M-H simulation is conducted with the
blocks
may be easy to
derive. Then, a multiple-block M-H simulation is conducted with the
blocks
![]() and
and
![]() leading to the sample
leading to the sample
To demonstrate this technique in action, we return to the probit regression example discussed in Sect. 3.3.2 to show how a MCMC sampler can be developed with the help of latent variables. The approach, introduced by [1], capitalizes on the simplifications afforded by introducing latent or auxiliary data into the sampling.
The model is rewritten as
| (3.26) |
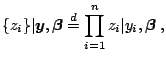 |
The results, based on ![]() MCMC draws beyond a burn-in of
a
MCMC draws beyond a burn-in of
a ![]() iterations, are reported in Fig. 3.4. The results
are close to those presented above, especially to the ones from the
tailored M-H chain.
iterations, are reported in Fig. 3.4. The results
are close to those presented above, especially to the ones from the
tailored M-H chain.
![\includegraphics[width=9cm]{text/2-3/fig3press.eps}](img1393.gif)
|