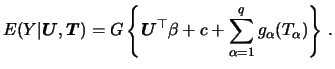9.3 Generalized Additive Partial Linear Models

The most complex form of generalized models that we consider here is the GAPLM

$\displaystyle E(Y\vert{\boldsymbol{U}},{\boldsymbol{T}}) = G \left\{ {\boldsymbol{U}}^\top \beta + c +\sum_{\alpha =1}^q g_\alpha (T_\alpha ) \right\}\,.$ (9.16)

The estimation of this model involves all techniques that were previously introduced. We are particularly interested in estimating the parameter $ \beta$ at $ \sqrt{n}$-rate and the component functions $ g_\alpha$ with the rate that is typical for the dimension of $ T_\alpha$.

9.3.1 GAPLM using Backfitting

For model (9.16), the backfitting and local scoring procedures from Subsection 9.2.1 can be directly used. Since we have a link function $ G$, the local scoring algorithm is used without any changes. For the ``inner'' backfitting iteration, the algorithm is adapted to a combination of parametric (linear) regression and additive modeling. Essentially, the weighted smoother matrix $ {\mathbf{S}}_\alpha (\bullet \vert {\boldsymbol{w}})$ is replaced by a weighted linear projection matrix

$\displaystyle {\mathbf{P}}_w = {\mathbf{U}}({\mathbf{U}}^\top {\mathbf{W}}{\mathbf{U}})^{-1} {\mathbf{U}}^\top {\mathbf{W}}$

for the linear component. Here $ {\mathbf{W}}$ is the weight matrix from Subsection 9.2.1 and $ {\mathbf{U}}$ is the design matrix obtained from the observations of $ {\boldsymbol{U}}$. We refer for further details to Hastie & Tibshirani (1990).

9.3.2 GAPLM using Marginal Integration

The marginal integration approach for (9.16) is a subsequent application of the semiparametric ML procedure for the GPLM (see Chapter 7), followed by marginal integration (as introduced in Chapter 8) applied on the nonparametric component of the GPLM. For this reason we only sketch the complete procedure and refer for the details to Härdle et al. (2004).

The key idea for estimating the GAPLM is the following: We use the profile likelihood estimator for the GPLM with a modification of the local likelihood function (7.8):

$\displaystyle { \ell_{h,{\mathbf{H}}}({\boldsymbol{Y}},{\boldsymbol{\mu}}_{m({\boldsymbol{T}})},\phi) }$
$\displaystyle \quad$ $\displaystyle =$ $\displaystyle \sum_{i=1}^n K_{h}(t_\alpha-{\boldsymbol{T}}_{\alpha}) {\mathcal{... ...bol{\beta}}+m(t_\alpha, {\boldsymbol{t}}_{\underline{\alpha}})\},\phi\right)\,.$  

As for the GPLM this local likelihood is maximized with respect to the nonparametric component $ m_{\boldsymbol{\beta}}(t_\alpha,{\boldsymbol{t}}_{\underline{\alpha}})$, this gives an estimate that does not (yet) make use of th additive structure.

We apply the now marginal integration method to this pre-estimate. The final estimator is

$\displaystyle \widehat {g}_\alpha (t_\alpha) = {1 \over n} \sum_{l=1}^n \wideha... ..._{l=1}^n \widehat{m} (T_{i\alpha} , {\boldsymbol{T}}_{l\underline{\alpha}} )\,.$ (9.18)

To avoid numerical problems, in particular at boundary regions or in regions of sparse data, a weight function should be applied inside the averaging. More precisely, the final estimate should calculated by:

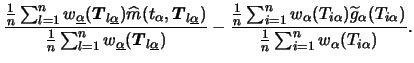$\displaystyle \widehat {g}_\alpha (t_\alpha)$ $\displaystyle =$ $\displaystyle {{1 \over n} \sum_{l=1}^n w_{\underline{\alpha}} ({\boldsymbol{T}... ...g}_\alpha (T_{i\alpha}) \over {1 \over n} \sum_{i=1}^n w_\alpha (T_{i\alpha})}.$  

Finally, the constant $ c$ is estimated by

$\displaystyle \widehat c = {1 \over n} \sum_{i=1}^n \widehat {m} ({\boldsymbol{... ...\sum_{i=1}^n \widehat {m} (T_{i\alpha},{\boldsymbol{T}}_{i\underline{\alpha}}).$ (9.19)

For these estimators we have asymptotic properties according to the following theorem.

THEOREM 9.3  
Suppose the bandwidths tend to zero and fulfill $ {\mathbf{H}}=\widetilde{h}{\mathbf{I}}$, $ n h \widetilde{h}^{2(q-1)}/\log^2(n)\to\infty$, then under some smoothness and regularity conditions

$\displaystyle \sqrt {nh} \{ \widehat g_\alpha (t_\alpha) - g_\alpha(t_\alpha)\... ...hop{\longrightarrow}\limits_{}^{L}} N(b_\alpha (t_\alpha),v_\alpha(t_\alpha)).$

The expressions for bias and variance are quite complex such that we omit them here. We remark that the correlation between the estimates of the components are of higher order rate. Consequently, summing up the estimates would give us a consistent estimate of the index function $ m$ with the one-dimensional nonparametric rate.

Härdle et al. (2004) also state that the bias for the estimates $ \widehat g_\alpha$ is not negligible. Therefore they propose a bias correction procedure using (wild) bootstrap.

EXAMPLE 9.2  

To illustrate the GAPLM estimation we use the data set as in Example 5.1 selecting the most southern state (Sachsen) of East Germany. Recall that the data comprise the following explanatory variables:

$ U_1$
family/friend in West,
$ U_2$
unemployed/job loss certain,
$ U_3$
middle sized city (10,000-100,000 habitants),
$ U_4$
female (1 if yes),
$ T_1$
age of person (in years),
$ T_2$
household income (in DM).

Figure 9.3: Density plots for migration data (subsample from Sachsen), AGE on the left, HOUSEHOLD INCOME on the right
\includegraphics[width=1.3\defpicwidth]{SPMmigsd.ps}


Table 9.2: Descriptive statistic for migration data (subsample from Sachsen, $ n=955$)
    Yes No (in %)  
$ Y$ MIGRATION INTENTION 39.6 60.4    
$ U_1$ FAMILY/FRIENDS 82.4 27.6    
$ U_2$ UNEMPLOYED/JOB LOSS 18.3 81.7    
$ U_3$ CITY SIZE 26.0 74.0    
$ U_4$ FEMALE 51.6 48.4    
    Min Max Mean S.D.
$ T_1$ AGE 18 65 40.37 12.69
$ T_2$ INCOME 200 4000 2136.31 738.72


Table 9.3: Logit and GAPLM coefficients for migration data
  GLM GAPLM
  Coefficients S.E. $ p$-values Coefficients
        $ h=0.75$ $ h=1.00$
FAMILY/FRIENDS 0.7604 0.1972 $ <$0.001 0.7137 0.7289
UNEMPLOYED/JOB LOSS 0.1354 0.1783 0.447 0.1469 0.1308
CITY SIZE 0.2596 0.1556 0.085 0.3134 0.2774
FEMALE -0.1868 0.1382 0.178 -0.1898 -0.1871
AGE (stand.) -0.5051 0.0728 $ <$0.001 -- --
INCOME (stand.) 0.0936 0.0707 0.187 -- --
constant -1.0924 0.2003 $ <$0.001 -1.1045 -1.1007

We first show the density plots for the two continuous variables in Figure 9.3. Table 9.2 gives descriptive statistics for the data. In the following, AGE and INCOME have been standardized which corresponds to multiplying the bandwidths with the empirical standard deviations.

Table 9.3 presents on the left the results of a parametric logit estimation. Obviously, AGE has a significant linear impact on the migration intention whereas this does not hold for household income. On the right hand side of Table 9.3 we have listed the results for the linear part of the GAPLM. Since the choice of bandwidths can be crucial, we used two different bandwidths for the estimation. We see that the coefficients for the GAPLM show remarkable differences with respect to the logit coefficients. We can conclude that the impact of family/friends in the West seems to be overestimated by the parametric logit whereas the city size effect is larger for the semiparametric model. The nonparametric function estimates for AGE and INCOME are displayed in Figure 9.4.

Figure 9.4: Additive curve estimates for AGE (left) and INCOME (right) in Sachsen (upper plots with $ h=0.75$, lower with $ h=1.0$)
\includegraphics[width=1.3\defpicwidth]{SPMmigsf.ps}

In contrast to Example 7.1 the GAPLM allows us to include both, AGE and INCOME, as univariate nonparametric functions. The interpretation of these functions is much easier. We can easily see that the component function for AGE is clearly monotone decreasing. The nonparametric impact of INCOME, however, does not vanish when the bandwidth is increased. We will come back to this point when testing functional forms in such models in the following section. $ \Box$