12.2 Discrimination Rules in Practice
The ML rule is used if the distribution of the data is known up to
parameters. Suppose for example that the data come from multivariate
normal distributions
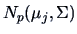 .
If we have
.
If we have 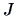 groups with
groups with 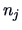 observations in each group, we use
observations in each group, we use 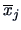 to estimate
to estimate
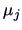 , and
, and 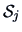 to estimate
to estimate 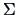 . The common
covariance may be estimated by
. The common
covariance may be estimated by
 |
(12.9) |
with
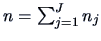 .
Thus the empirical version of the ML rule of Theorem 12.2
is to allocate a new observation
.
Thus the empirical version of the ML rule of Theorem 12.2
is to allocate a new observation 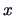 to
to 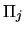 such
that
such
that 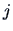 minimizes
minimizes
EXAMPLE 12.4
Let us apply this rule to the Swiss bank notes. The 20
randomly chosen bank notes which we had clustered into two groups in
Example
11.6 are used.
First the covariance
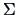
is estimated by the average of the covariances
of
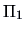
(cluster 1) and
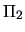
(cluster 2).
The hyperplane
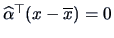
which separates the two populations is given by
Now let us apply the discriminant rule to the entire bank notes data set.
Counting the number of misclassifications by
we obtain 1 misclassified observation for the conterfeit bank notes and
0 misclassification for the genuine bank notes.
When  groups, the allocation regions can be calculated using
groups, the allocation regions can be calculated using
The rule is to allocate
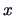
to
Misclassification probabilities are given by (12.7)
and can be estimated by replacing the unknown parameters by their
corresponding estimators.
For the ML rule for two normal populations we obtain
where
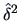 =
=
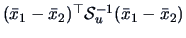 is the estimator for
is the estimator for 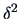 .
.
The probabilities of misclassification may also be
estimated by the re-substitution method. We reclassify each
original observation 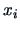 ,
, 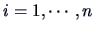 into
into
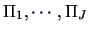 according to the chosen rule. Then denoting the number of
individuals coming from
according to the chosen rule. Then denoting the number of
individuals coming from 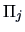 which have been classified into
which have been classified into 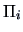 by
by 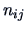 ,
we have
,
we have
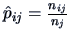 ,
an estimator of
,
an estimator of 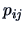 . Clearly, this
method leads to too optimistic estimators of
. Clearly, this
method leads to too optimistic estimators of 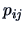 , but it provides
a rough measure of the quality of the discriminant rule.
The matrix
, but it provides
a rough measure of the quality of the discriminant rule.
The matrix
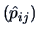 is called the
confussion matrix in
Johnson and Wichern (1998).
is called the
confussion matrix in
Johnson and Wichern (1998).
The apparent error rate (APER) is defined as the fraction of observations
that are misclassified. The APER, expressed as a percentage, is
For the calculation of the APER we use the observations twice:
the first time to construct
the classification rule and the second time to evaluate this rule.
An APER of 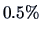 might therefore be too optimistic.
An approach that corrects for this bias is based on the holdout procedure of Lachenbruch and Mickey (1968).
For two populations this procedure is as follows:
might therefore be too optimistic.
An approach that corrects for this bias is based on the holdout procedure of Lachenbruch and Mickey (1968).
For two populations this procedure is as follows:
- 1.
- Start with the first population
 . Omit one observation and develop
the classification rule based on the remaining
. Omit one observation and develop
the classification rule based on the remaining 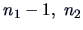 observations.
observations.
- 2.
- Classify the ``holdout'' observation using the discrimination rule in Step 1.
- 3.
- Repeat steps 1 and 2 until all of the
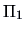 observations are classified.
Count the number
observations are classified.
Count the number 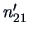 of misclassified observations.
of misclassified observations.
- 4.
- Repeat steps 1 through 3 for population
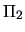 . Count the number
. Count the number 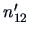 of misclassified observations.
of misclassified observations.
Estimates of the misclassification probabilities are given by
and
A more realistic estimator of the actual error rate (AER) is given by
 |
(12.10) |
Statisticians favor the AER (for its unbiasedness) over the APER.
In large samples, however, the computational
costs might counterbalance the statistical advantage. This is not a real
problem since the two misclassification measures are asymptotically
equivalent.
 MVAaer.xpl
MVAaer.xpl
Fisher's linear discrimination function
Another approach stems from R. A. Fisher. His idea was to base the discriminant rule on
a projection 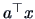 such that a good separation was achieved.
This LDA projection method is called
Fisher's linear discrimination function.
If
such that a good separation was achieved.
This LDA projection method is called
Fisher's linear discrimination function.
If
denotes a linear combination of observations,
then the total sum of squares of 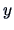 ,
,
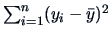 , is
equal to
, is
equal to
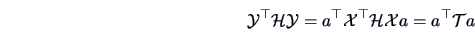 |
(12.11) |
with the centering matrix
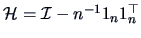 and
and
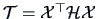 .
.
Suppose we have samples 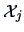 ,
, 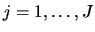 , from
, from 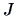 populations.
Fisher's suggestion was to find the linear combination
populations.
Fisher's suggestion was to find the linear combination
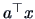 which maximizes the ratio of the between-group-sum of
squares to the within-group-sum of squares.
which maximizes the ratio of the between-group-sum of
squares to the within-group-sum of squares.
The within-group-sum of squares is given by
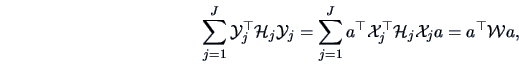 |
(12.12) |
where 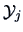 denotes the
denotes the 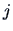 -th sub-matrix of
-th sub-matrix of 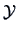 corresponding
to observations of group
corresponding
to observations of group 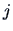 and
and 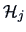 denotes the
denotes the
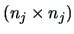 centering matrix. The within-group-sum of squares
measures the sum of variations within each group.
centering matrix. The within-group-sum of squares
measures the sum of variations within each group.
The between-group-sum of squares is
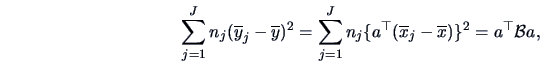 |
(12.13) |
where
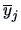 and
and
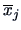 denote the means of
denote the means of
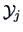 and
and 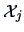 and
and 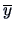 and
and 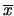 denote the sample means of
denote the sample means of 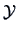 and
and  .
The between-group-sum of squares
measures the variation of the means across groups.
.
The between-group-sum of squares
measures the variation of the means across groups.
The total sum of squares (12.11) is the sum of the
within-group-sum of squares and the between-group-sum of squares, i.e.,
Fisher's idea was to select a projection vector 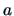 that maximizes the ratio
that maximizes the ratio
 |
(12.14) |
The solution is found by applying Theorem 2.5.
THEOREM 12.4
The vector
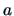
that maximizes (
12.14) is the eigenvector of
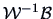
that corresponds to the largest eigenvalue.
Now a discrimination rule is easy to obtain:
classify 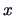 into group
into group 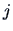 where
where
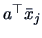 is
closest to
is
closest to 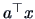 , i.e.,
, i.e.,
When 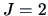 groups, the discriminant rule is easy to compute.
Suppose that group 1 has
groups, the discriminant rule is easy to compute.
Suppose that group 1 has 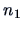 elements and group 2 has
elements and group 2 has 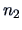 elements.
In this case
elements.
In this case
where
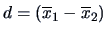 .
.
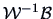 has only one eigenvalue which equals
has only one eigenvalue which equals
and the corresponding eigenvector is
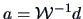 .
The corresponding discriminant rule is
.
The corresponding discriminant rule is
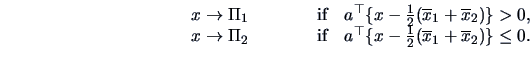 |
(12.15) |
The Fisher LDA is closely related to projection pursuit (Chapter 18)
since the statistical technique is based on a one dimensional
index 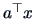 .
.
EXAMPLE 12.6
Consider the bank notes data again.
Let us use the subscript ``g'' for the genuine and ``f'' for the
conterfeit bank notes, e.g.,
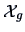
denotes the first hundred
observations of

and
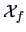
the second hundred.
In the context of the bank data set the ``between-group-sum of squares''
is defined as
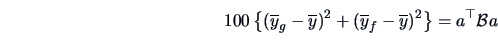 |
(12.16) |
for some matrix
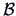
. Here,
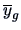
and
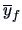
denote the means for the genuine and counterfeit bank
notes and
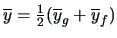
.
The ``within-group-sum of squares'' is
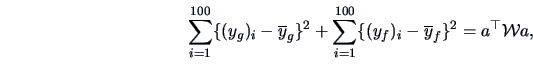 |
(12.17) |
with
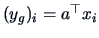
and
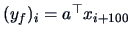
for
.
Figure 12.2:
Densities of projections of genuine
and counterfeit bank notes by
Fisher's discrimination rule.
 MVAdisfbank.xpl
MVAdisfbank.xpl
|
|
The resulting discriminant rule consists of allocating an observation 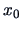 to the genuine sample space if
to the genuine sample space if
with
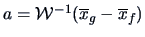
(see Exercise
12.8) and of allocating
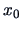
to the
counterfeit sample space when the opposite is true.
In our case
One genuine and no counterfeit bank notes are misclassified.
Figure
12.2 shows the estimated densities for
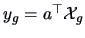
and
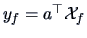
. They are
separated better than those of the diagonals in Figure
1.9.
Note that the allocation rule (12.15) is exactly the same as the ML rule
for 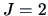 groups and for normal distributions with the same covariance.
For
groups and for normal distributions with the same covariance.
For 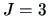 groups this rule will be different, except for the special case
of collinear sample means.
groups this rule will be different, except for the special case
of collinear sample means.
Summary

-
A discriminant rule is a separation of the sample space into sets
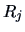 .
An observation
.
An observation 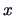 is classified as coming from population
is classified as coming from population 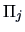 if it
lies in
if it
lies in 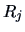 .
.

-
The expected cost of misclassification (ECM) for two populations
is given by ECM
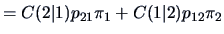 .
.

-
The ML rule is applied if the distributions in the populations are
known up to parameters, e.g., for normal distributions
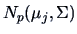 .
.

-
The ML rule allocates
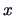 to the population that exhibits the smallest
Mahalanobis distance
to the population that exhibits the smallest
Mahalanobis distance

-
The probability of misclassification is given by
where 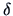 is the Mahalanobis distance between
is the Mahalanobis distance between 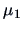 and
and 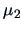 .
.

-
Classification for different covariance structures in the two populations
leads to quadratic discrimination rules.

-
A different approach is Fisher's linear discrimination rule which
finds a linear combination
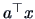 that maximizes the ratio
of the ``between-group-sum of squares''
and the ``within-group-sum of squares''.
This rule turns out to be identical to the ML rule when
that maximizes the ratio
of the ``between-group-sum of squares''
and the ``within-group-sum of squares''.
This rule turns out to be identical to the ML rule when
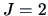 for normal populations.
for normal populations.
![]() .
If we have
.
If we have ![]() groups with
groups with ![]() observations in each group, we use
observations in each group, we use ![]() to estimate
to estimate
![]() , and
, and ![]() to estimate
to estimate ![]() . The common
covariance may be estimated by
. The common
covariance may be estimated by

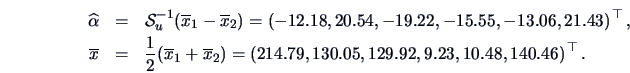
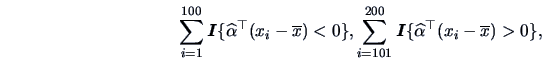
![]() groups, the allocation regions can be calculated using
groups, the allocation regions can be calculated using
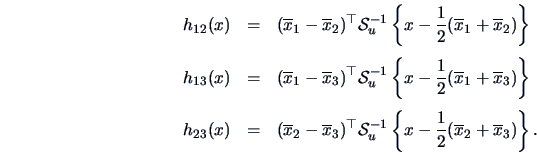
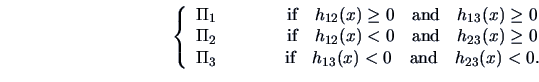

![]() ,
, ![]() into
into
![]() according to the chosen rule. Then denoting the number of
individuals coming from
according to the chosen rule. Then denoting the number of
individuals coming from ![]() which have been classified into
which have been classified into ![]() by
by ![]() ,
we have
,
we have
![]() ,
an estimator of
,
an estimator of ![]() . Clearly, this
method leads to too optimistic estimators of
. Clearly, this
method leads to too optimistic estimators of ![]() , but it provides
a rough measure of the quality of the discriminant rule.
The matrix
, but it provides
a rough measure of the quality of the discriminant rule.
The matrix
![]() is called the
confussion matrix in
Johnson and Wichern (1998).
is called the
confussion matrix in
Johnson and Wichern (1998).



![]() ,
, ![]() , from
, from ![]() populations.
Fisher's suggestion was to find the linear combination
populations.
Fisher's suggestion was to find the linear combination
![]() which maximizes the ratio of the between-group-sum of
squares to the within-group-sum of squares.
which maximizes the ratio of the between-group-sum of
squares to the within-group-sum of squares.
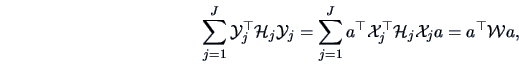
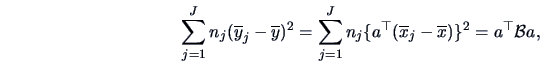
![]() into group
into group ![]() where
where
![]() is
closest to
is
closest to ![]() , i.e.,
, i.e.,
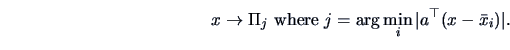
![]() groups, the discriminant rule is easy to compute.
Suppose that group 1 has
groups, the discriminant rule is easy to compute.
Suppose that group 1 has ![]() elements and group 2 has
elements and group 2 has ![]() elements.
In this case
elements.
In this case
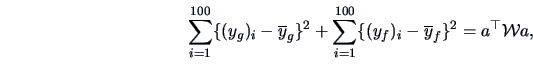
![\includegraphics[width=1\defpicwidth]{discbfis.ps}](mvahtmlimg3512.gif)
![]() to the genuine sample space if
to the genuine sample space if
![]() groups and for normal distributions with the same covariance.
For
groups and for normal distributions with the same covariance.
For ![]() groups this rule will be different, except for the special case
of collinear sample means.
groups this rule will be different, except for the special case
of collinear sample means.
