In the past fifteen years computational statistics has been enriched by a powerful, somewhat abstract method of generating variates from a target probability distribution that is based on Markov chains whose stationary distribution is the probability distribution of interest. This class of methods, popularly referred to as Markov chain Monte Carlo methods, or simply MCMC methods, have been influential in the modern practice of Bayesian statistics where these methods are used to summarize the posterior distributions that arise in the context of the Bayesian prior-posterior analysis ([58,23,56,59,3,14], 1996; [31,57,22,50,5,10,12,18,34,49,25]). MCMC methods have proved useful in practically all aspects of Bayesian inference, for example, in the context of prediction problems and in the computation of quantities, such as the marginal likelihood, that are used for comparing competing Bayesian models.
A central reason for the widespread interest in MCMC methods is that
these methods are extremely general and versatile and can be used to
sample univariate and multivariate distributions when other methods
(for example classical methods that produce independent and
identically distributed draws) either fail or are difficult to
implement. The fact that MCMC methods produce dependent draws causes
no substantive complications in summarizing the target
distribution. For example, if
![]() are draws from a (say continuous) target
distribution
are draws from a (say continuous) target
distribution
![]() , where
, where
![]() ,
then the expectation of
,
then the expectation of
![]() under
under ![]() can be
estimated by the average
can be
estimated by the average
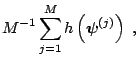 |
(3.1) |
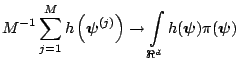 d d |
Another reason for the interest in MCMC methods is that, somewhat
surprisingly, it is rather straightforward to construct one or more
Markov chains whose limiting invariant distribution is the desired
target distribution. One way to construct the appropriate Markov chain
is by a method called the
Metropolis method which was introduced by [39] in connection
with work related to the hydrogen bomb project. In this method, the
Markov chain simulation is constructed by a recursive two step
process. Given the current iterate
![]() , a proposal
value
, a proposal
value
![]() is drawn from a distribution
is drawn from a distribution
![]() , such that
, such that
![]() is
symmetrically distributed about the current value
is
symmetrically distributed about the current value
![]() . In the second step, this proposal value is
accepted as the next iterate
. In the second step, this proposal value is
accepted as the next iterate
![]() of the
Markov chain with probability
of the
Markov chain with probability
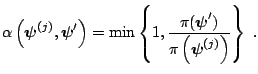 |
The requirement that the proposal distribution be symmetric about the current value was relaxed by [32]. The resulting method, commonly called the Metropolis-Hastings (M-H) method, relies on the same two steps of the Metropolis method except that the probability of move is given by
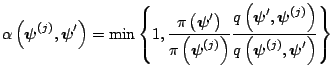 |
In applications when the dimension of
![]() is large it may
be preferable to construct the Markov chain simulation by first
grouping the variables
is large it may
be preferable to construct the Markov chain simulation by first
grouping the variables
![]() into smaller
blocks. For simplicity suppose that two blocks are adequate and that
into smaller
blocks. For simplicity suppose that two blocks are adequate and that
![]() is written as
is written as
![]() ,
with
,
with
![]() . In that
case, the M-H chain can be constructed by
. In that
case, the M-H chain can be constructed by
Despite the long vintage of the M-H method, the contemporary interest
in MCMC methods was sparked by work on a related MCMC method, the
Gibbs sampling algorithm. The Gibbs sampling algorithm is one of the
simplest Markov chain Monte Carlo algorithms and has its origins in
the work of [2] on spatial lattice systems, [26]
on the problem of image processing, and [58] on missing
data problems. The paper by [23] helped to demonstrate the
value of the Gibbs algorithm for a range of problems in Bayesian
analysis. In the Gibbs sampling method, the Markov chain is
constructed by simulating the conditional distributions that are
implied by
![]() . In particular, if
. In particular, if
![]() is
split into two components
is
split into two components
![]() and
and
![]() ,
then the Gibbs method proceeds through the recursive sampling of the
conditional distributions
,
then the Gibbs method proceeds through the recursive sampling of the
conditional distributions
![]() and
and
![]() , where the most recent
value of
, where the most recent
value of
![]() is used in the first simulation and the
most recent value of
is used in the first simulation and the
most recent value of
![]() in the second
simulation. This method is most simple to implement when each
conditional distribution is a known distribution that is easy to
sample. As we show below, the Gibbs sampling method is a special case
of the multiple block M-H algorithm.
in the second
simulation. This method is most simple to implement when each
conditional distribution is a known distribution that is easy to
sample. As we show below, the Gibbs sampling method is a special case
of the multiple block M-H algorithm.
The rest of the chapter is organized as follows. In Sect. 3.2 we summarize the relevant Markov chain theory that justifies simulation by MCMC methods. In particular, we provide the conditions under which discrete-time and continuous state space Markov chains satisfy a law of large numbers and a central limit theorem. The M-H algorithm is discussed in Sect. 3.3 followed by the Gibbs sampling algorithm in Sect. 3.4. Section 3.5 deals with MCMC methods with latent variables and Sect. 3.6 with ways of estimating the marginal densities based on the MCMC output. Issues related to sampler performance are considered in Sect. 3.7 and strategies for improving the mixing of the Markov chains in Sect. 3.8. Section 3.9 concludes with brief comments about new and emerging directions in MCMC methods.